Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
MagnetostatikDie Magnetostatik ist ein Teilgebiet der Elektrodynamik. Sie behandelt zeitlich konstante Magnetfelder (Magnetische Gleichfelder). In der Magnetostatik wird die räumliche Verteilung von Magnetfeldern in der Umgebung von Dauermagneten und von stationären Strömen (Konzept des Stromfadens) untersucht. Hierzu gehören neben den einzelnen magnetischen Eigenschaften der Stoffe wie Ferromagnetismus, Diamagnetismus etc. auch das Erdmagnetfeld. Außerdem beinhaltet die Magnetostatik die Kraftwirkung derartig erzeugter Felder auf Magnete und Ströme. Hierzu gehört das Verhalten eines magnetischen Dipols in einem zeitlich konstanten Magnetfeld; beispielsweise das Verhalten einer (frei beweglichen) Magnetnadel im Erdmagnetfeld. Die Grundbegriffe sind der Elektrostatik analog. Der positiven und negativen elektrischen Ladung entspricht Nordpol und Südpol bzw. positive und negative Polstärke eines Magneten. Im Gegensatz zur Elektrostatik können magnetische Polstärken nicht isoliert werden, sondern treten in einem Körper immer zusammen auf. Produkt-HighlightFür zeitlich konstante Felder entkoppeln die Gleichungen für E- und B-Felder. Setzt man in den Maxwellgleichungen alle Zeitableitungen gleich 0, so entstehen Gleichungen, die nicht gleichzeitig E und B enthalten. Die Phänomene der Magnetostatik lassen sich mit folgenden zwei reduzierten Maxwellgleichungen beschreiben: I) II) Man führt das Vektorpotential Dadurch wird automatisch die Gleichung
da die Rotation des Gradienten eines Skalarfeldes verschwindet.
Setzt man ein, so ergibt sich mit der Coulomb-Eichung Dies stellt für jede Komponente eine Poisson-Gleichung dar, die durch gelöst wird. Wendet man die Rotation auf A an so erhält man das Biot-Savart-Gesetz für das physikalisch relevante B-Feld Für einen Stromfaden geht Literatur
|
| Dieser Artikel basiert auf dem Artikel Magnetostatik aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




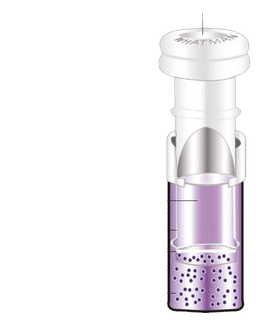
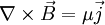
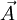 als Hilfsfeld mit folgender Definition ein:
als Hilfsfeld mit folgender Definition ein:

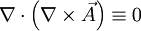 .
.
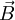 invariant ist unter einer Eichtransformation
invariant ist unter einer Eichtransformation 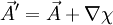 . D.h. die durch A und A' festgelegten B-Felder sind identisch. Dies ergibt sich aus
. D.h. die durch A und A' festgelegten B-Felder sind identisch. Dies ergibt sich aus
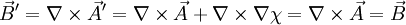 ,
,
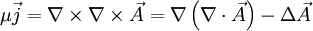
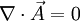 die besonders einfache Form:
die besonders einfache Form:
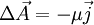
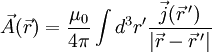
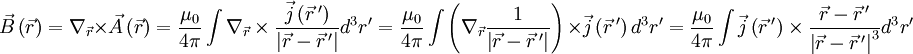
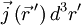 zu
zu 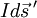 über:
über: