Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
ElektrodynamikDie klassische Elektrodynamik (KED) oder Elektrodynamik ist ein Teilgebiet der Physik, das sich mit elektrischen und magnetischen Feldern und Potentialen, sowie der Dynamik elektrisch geladener Objekte und den von ihnen hervorgerufenen elektromagnetischen Wellen beschäftigt. Die klassische Elektrodynamik wurde von J. C. Maxwell Ende des 19. Jahrhunderts formuliert. Anfang des 20. Jahrhunderts stellte sich heraus, dass es sich bei der Elektrodynamik um eine relativistische Theorie handelt, sie also bereits die Gesetze der speziellen Relativitätstheorie erfüllte, noch ehe es diese gab. Durch Arbeiten von Hendrik Antoon Lorentz, Henri Poincaré, Albert Einstein und insbesondere Hermann Minkowski konnte die Elektrodynamik daher auf Basis des neuen relativistischen Weltbildes sowohl interpretiert als auch erweitert werden. Im Laufe der 1940er Jahre gelang es schließlich die Quantenmechanik mit der Relativitätstheorie zu kombinieren und eine Quantenfeldtheorie des Elektromagnetismus zu formulieren, welche als Quantenelektrodynamik (QED) bezeichnet wird. Sie ist die heute durch Experimente am genauesten überprüfte Theorie der Physik. Produkt-Highlight
Die TheorieDie Elektrodynamik basiert auf den Maxwellgleichungen, die das Zusammenspiel von elektrischen und magnetischen Feldern mit elektrischen Ladungsträgern beschreiben. Sie wird „klassisch“ genannt, da sie quantenmechanische Aspekte nicht berücksichtigt. Die grundlegenden vier Maxwellgleichung lauten in „cgs“-Einheiten in ihrer Kurzform (in den gebräuchlichen „mksA“-Einheiten sehen die Gleichungen nur geringfügig anders aus, man erhält sie formal mit sowie
Dass das Vektorpotential in beiden Feldern auftritt, legt nahe, dass elektrisches und magnetisches Feld in Wirklichkeit zwei Erscheinungsformen eines einzigen Feldes, des so genannten elektromagnetischen Feldes sind. In der relativistischen Formulierung der Elektrodynamik wird dies unmittelbar deutlich, da die beiden Felder als Komponenten einer einzigen Größe, des (schief-symmetrischen!) elektromagnetischen Feldtensors auftreten. Durch das elektrische und magnetische Feld werden die Potentiale nicht eindeutig festgelegt, das heißt, es gibt verschiedene Φ und wobei Nach dem Noether-Theorem gehört zu jeder kontinuierlichen Symmetrie eine Erhaltungsgröße. Die Eichinvarianz ist eine kontinuierliche Symmetrie, und die zugehörige Erhaltungsgröße ist gerade die elektrische Ladung. Spezialfälle der ElektrodynamikDie Elektrostatik ist der Spezialfall unbewegter elektrischer Ladungen und statischer (sich nicht mit der Zeit ändernder) elektrischer Felder. Sie kann aber in Grenzen auch verwendet werden, solange die Geschwindigkeiten und Beschleunigungen der Ladungen und die Änderungen der Felder klein sind. Die Magnetostatik beschäftigt sich mit dem Spezialfall konstanter Ströme in insgesamt ungeladenen Leitern und konstanter Magnetfelder. Sie kann aber ebenfalls für hinreichend langsam veränderliche Ströme und Magnetfelder verwendet werden. Die Kombination aus beiden, Elektromagnetismus, könnte beschrieben werden als Elektrodynamik der nicht zu stark beschleunigten Ladungen. Die meisten Vorgänge in elektrischen Schaltkreisen (z. B. Spule, Kondensator, Transformator) lassen sich bereits auf dieser Ebene beschreiben. Ein stationäres elektrisches oder magnetisches Feld bleibt nahe seiner Quelle, wie zum Beispiel das Erdmagnetfeld. Ein sich veränderndes elektromagnetisches Feld kann sich jedoch von seinem Ursprung entfernen. Das Feld bildet eine elektromagnetische Welle im Zusammenspiel zwischen magnetischem und elektrischem Feld. Diese Abstrahlung elektromagnetischer Wellen wird in der Elektrostatik vernachlässigt. Die Beschreibung des elektromagnetischen Feldes beschränkt sich hier also auf das Nahfeld. Elektromagnetische Wellen hingegen sind die einzige Form des elektromagnetischen Feldes, die auch unabhängig von einer Quelle existieren kann. Sie werden zwar von Quellen erzeugt, können aber nach ihrer Erzeugung unabhängig von der Quelle weiterexistieren. Da Licht sich als elektromagnetische Welle beschreiben lässt, ist auch die Optik letztlich ein Spezialfall der Elektrodynamik. Elektrodynamik und RelativitätstheorieIm Gegensatz zur klassischen Mechanik ist die Elektrodynamik nicht galilei-invariant. Das bedeutet, wenn man, wie in der klassischen Mechanik, einen absoluten, euklidischen Raum und eine davon unabhängige absolute Zeit annimmt, dann gelten die Maxwellgleichungen nicht in jedem Inertialsystem. Einfaches Beispiel: Ein mit konstanter Geschwindigkeit fliegendes, geladenes Teilchen ist von einem elektrischen und einem magnetischen Feld umgeben. Ein mit gleicher Geschwindigkeit fliegendes, gleichgeladenes Teilchen erfährt durch das elektrische Feld eine abstoßende Kraft, da sich gleichnamige Ladungen gegenseitig abstoßen; gleichzeitig erfährt es durch das Magnetfeld eine anziehende Lorentzkraft, die die Abstoßung teilweise kompensiert. Bei Lichtgeschwindigkeit wäre diese Kompensation vollständig. In dem Inertialsystem, in dem beide Teilchen ruhen, gibt es kein magnetisches Feld und damit keine Lorentzkraft. Dort wirkt nur die abstoßende Coulombkraft, so dass das Teilchen stärker beschleunigt wird, als im ursprünglichen Bezugssystem, in dem sich beide Ladungen bewegen. Dies widerspricht der newtonschen Physik, bei der die Beschleunigung nicht vom Bezugssystem abhängt. Diese Erkenntnis führte zunächst zur Annahme, in der Elektrodynamik gebe es ein bevorzugtes Bezugssystem (Äthersystem). Versuche, die Geschwindigkeit der Erde gegen den Äther zu messen, zum Beispiel das Michelson-Morley-Experiment, schlugen jedoch fehl. Hendrik Antoon Lorentz löste dieses Problem mit einer modifizierten Lorentzschen Äthertheorie, wobei dessen Erklärung jedoch von Albert Einstein mit seiner speziellen Relativitätstheorie abgelöst wurde. Einstein ersetzte Newtons absoluten Raum und absolute Zeit durch eine vierdimensionale Raumzeit. In der Relativitätstheorie tritt an die Stelle der Galilei-Invarianz die Lorentz-Invarianz, die von der Elektrodynamik erfüllt wird. In der Tat lässt sich die Verringerung der Beschleunigung und damit die magnetische Kraft im obigen Beispiel über eine Rücktransformation der Beobachtungen im bewegten System in das ruhende System als Folge der Längenkontraktion und Zeitdilatation erklären. In gewisser Weise lässt sich daher die Existenz von magnetischen Phänomenen letztlich auf die Struktur von Raum und Zeit zurückführen, wie sie in der Relativitätstheorie beschrieben wird. Unter diesem Gesichtspunkt erscheint auch die Struktur der Grundgleichungen für statische Magnetfelder mit ihren Kreuzprodukten weniger verwunderlich. In der relativistischen Beschreibung der Elektrodynamik bilden das skalare Potential und das Vektorpotential einen Vierervektor, analog zum Vierervektor von Raum und Zeit, so dass die Lorentz-Transformationen analog auch auf die elektromagnetischen Potentiale angewendet werden können. Bei einer speziellen Lorentz-Transformation mit der Geschwindigkeit v in z-Richtung gelten für die Felder in den gebräuchlichen „mksA“-Einheiten die Transformationsgleichungen:
(In cgs-Einheiten sind diese Gleichungen nur unwesentlich modifiziert: Man muss formal nur ErweiterungenJedoch ist auch die relativistische Elektrodynamik noch nicht widerspruchsfrei, auf kleinen Skalen ergeben sich Probleme wie die der Abraham-Lorentz-Gleichung. Die Quantenelektrodynamik (QED) vereint die Elektrodynamik deshalb mit quantenmechanischen Konzepten. Die Theorie der elektroschwachen Wechselwirkung vereinigt die QED mit der schwachen Wechselwirkung und ist Teil des Standardmodells der Elementarteilchenphysik. Die Struktur der QED ist ebenfalls Ausgangspunkt für die Quantenchromodynamik (QCD), welche die starke Wechselwirkung beschreibt. Allerdings ist die Situation dort noch komplizierter (z. B. drei Ladungsarten, siehe Farbladung). Eine Vereinheitlichung der Elektrodynamik mit der allgemeinen Relativitätstheorie (Gravitation) ist unter dem Namen Kaluza-Klein-Theorie bekannt, und stellt einen frühen Versuch zur Vereinheitlichung der fundamentalen Wechselwirkungen dar. Elektromagnetische SI-Einheiten
Die Umrechnung vom „cgs“-System, das vor allem in der Theoretischen Physik gebräuchlich ist, zum hier benutzten SI-System findet man systematisch hergeleitet und zusammengefasst u. a. im Anhang des im Folgenden angegebenen Buches von J. D. Jackson. Literatur
Siehe auch
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Elektrodynamik aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |



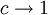 und
und 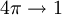 ; Einzelheiten der nicht ganz trivialen Umrechnung zwischen den verschiedenen Maßsystemen findet man im Anhang der neuesten Auflage des unten angegebenen Lehrbuches von J. D. Jackson):
; Einzelheiten der nicht ganz trivialen Umrechnung zwischen den verschiedenen Maßsystemen findet man im Anhang der neuesten Auflage des unten angegebenen Lehrbuches von J. D. Jackson):
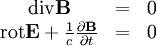
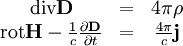 .
.
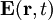 und
und 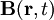 stehen hier für den elektrischen und den magnetischen Feldvektor.
stehen hier für den elektrischen und den magnetischen Feldvektor. 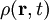 für eine beliebige Ladungsdichte im dreidimensionalen Raum und
für eine beliebige Ladungsdichte im dreidimensionalen Raum und 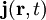 für die Bewegungen dieser Ladungsdichten in Form einer elektrischen Stromdichte.
für die Bewegungen dieser Ladungsdichten in Form einer elektrischen Stromdichte. 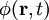 und ein
und ein 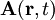 verwendet. Das elektrische und das magnetische Feld lassen sich durch diese Potentiale in „cgs“-Einheiten wie folgt ausdrücken
verwendet. Das elektrische und das magnetische Feld lassen sich durch diese Potentiale in „cgs“-Einheiten wie folgt ausdrücken

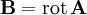
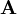 , die zu den gleichen Feldern, und somit zur gleichen Physik führen. Diese Eigenschaft der Potentiale nennt man Eichinvarianz, eichinvariante Theorien wie die Elektrodynamik nennt man Eichtheorien. Transformationen der Potentiale, die zu denselben Feldern führen, heißen Eichtransformationen. Die Eichtransformationen der Elektrodynamik lauten
, die zu den gleichen Feldern, und somit zur gleichen Physik führen. Diese Eigenschaft der Potentiale nennt man Eichinvarianz, eichinvariante Theorien wie die Elektrodynamik nennt man Eichtheorien. Transformationen der Potentiale, die zu denselben Feldern führen, heißen Eichtransformationen. Die Eichtransformationen der Elektrodynamik lauten
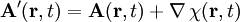
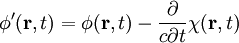
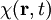 eine beliebige skalare Funktion ist.
eine beliebige skalare Funktion ist.
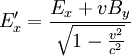
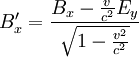
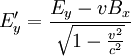
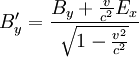
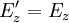
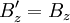
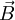 bzw.
bzw. 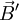 durch
durch 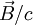 bzw.
bzw. 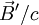 substituieren.)
substituieren.)


