Die Clifford-Algebra (nach William Kingdon Clifford) dient in der Mathematik und dort in der Differentialgeometrie sowie in der Quantenphysik der Definition der Spin-Gruppe und in ihren Darstellungen der Konstruktion von Spinorfeldern/bündeln, die wiederum zur Beschreibung von Elektronen und anderen Elementarteilchen sowie zur Bestimmung von Invarianten auf Mannigfaltigkeiten dienen.
Die Frage nach komplexen Einheiten
Es gibt in der Mathematik Zahlensysteme (Divisionsalgebra mit 1) mit komplexen Einheiten, genauer die komplexen Zahlen, die Quaternionen und Oktaven. In diesen können jeweils 1, 3 oder 7 Elemente 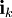 fixiert werden, welche mit der 1 zusammen den Zahlenraum als reellen Vektorraum aufspannen und welche (nicht nur) fixiert werden, welche mit der 1 zusammen den Zahlenraum als reellen Vektorraum aufspannen und welche (nicht nur) 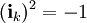 erfüllen. Manchmal reicht das nicht aus. Es werden zu einer beliebigen Anzahl n Strukturen gesucht, welche die reellen Zahlen und Elemente erfüllen. Manchmal reicht das nicht aus. Es werden zu einer beliebigen Anzahl n Strukturen gesucht, welche die reellen Zahlen und Elemente 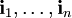 enthalten und in der ein Produkt ° definiert ist, welches die Bedingungen enthalten und in der ein Produkt ° definiert ist, welches die Bedingungen
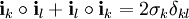
erfüllt, wobei δkl das Kroneckersymbol ist und 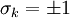 . .
Die Elemente 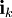 heißen die Erzeugenden oder Generatoren der Clifford-Algebra.
Das Produkt aller Erzeugenden wird durch ω bezeichnet, heißen die Erzeugenden oder Generatoren der Clifford-Algebra.
Das Produkt aller Erzeugenden wird durch ω bezeichnet,
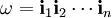 . Das Quadrat von ω
kann +1 oder -1 sein. . Das Quadrat von ω
kann +1 oder -1 sein.
Diese Struktur ist, bis auf die genannten Beispiele, kein Zahlensystem, sondern kann nur als Algebra realisiert werden, in welcher die 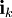 Erzeugende sind. Eine solche Algebra wird Clifford-Algebra genannt, nach William Kingdon Clifford, der sie im Jahr 1878 entdeckt hat. Sie wird mit Cl(p,q) oder Cl(p,q,ℝ) bezeichnet, falls Erzeugende sind. Eine solche Algebra wird Clifford-Algebra genannt, nach William Kingdon Clifford, der sie im Jahr 1878 entdeckt hat. Sie wird mit Cl(p,q) oder Cl(p,q,ℝ) bezeichnet, falls
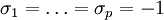 und und 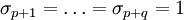
- und sonst keine algebraische Beziehung der Erzeugenden gilt.
Bis hierher haben wir formale Rechenregeln aufgestellt, wissen aber noch nichts über die Existenz, Eindeutigkeit und Struktur einer solchen Algebra. Dieses Problem ist sofort gelöst, wenn man die Clifford-Algebra als Teil einer reellen Matrixalgebra darstellen kann.
Beispiele
- Die komplexen Zahlen ℂ können als einfachste Clifford-Algebra Cl(1,0) mit einem einzigen Erzeugenden verstanden werden. Der Vektorraum V ist eindimensional von i erzeugt, die Algebra als Vektorraum zweidimensional von (1,i) erzeugt, die quadratische Funktion Q ist das Quadrat des Arguments. Die reelle Algebra ist die der 2x2-Matrizen
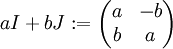 . .
- Die Quaternionen ergeben sich (nichttrivial) aus der Clifford-Algebra Cl(2,0). Die Erzeugenden (i,j) haben ein nichttriviales Produkt k=i°j, aus den definierenden Eigenschaften des Produkts ergibt sich, dass es mit dem Produkt der Quaternionen übereinstimmt. Der Vektorraum V ist reell zweidimensional, die Algebra reell vierdimensional. Eine Matrixdarstellung ist die Teilalgebra der komplexen 2x2-Matrizen
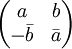 , ,
- durch Einsetzen der reellen 2x2-Matrizen der komplexen Zahlen a und b ergibt sich eine Teilalgebra der reellen 4x4-Matrizen.
- Cl(0,1) hat ein Erzeugendes i mit Quadrat 1. Daher können Elemente der reell 2-dimensionalen Algebra in zwei Summanden aufgespalten werden, von denen der erste unter Multiplikation mit i sein Vorzeichen behält und der zweite sein Vorzeichen ändert. In der Multiplikation zweier Elemente multiplizieren sich diese Summanden separat, wie in der Multiplikation zweier Diagonalmatrizen. Die Algebra ist also isomorph zur direkten Summe zweier Kopien von ℝ, Cl(0,1)≅ℝ⊕ℝ.
Überleitung
Im mathematischen Teil werden die Rechenregeln durch eine universelle Eigenschaft ergänzt und die Clifford-Algebra aus einer Tensoralgebra konstruiert. Es sei vorerst nur angemerkt, dass die Erzeugenden 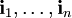 einen (Unter-)Vektorraum V der Dimension n=p+q innerhalb der Algebra aufspannen. Summiert man die definierende Eigenschaft über die Koordinatendarstellung eines Vektors einen (Unter-)Vektorraum V der Dimension n=p+q innerhalb der Algebra aufspannen. Summiert man die definierende Eigenschaft über die Koordinatendarstellung eines Vektors 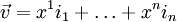 dieses Vektorraums, so ergibt sich eine koordinatenfreie (für Physiker: kovariante) Darstellung dieser: dieses Vektorraums, so ergibt sich eine koordinatenfreie (für Physiker: kovariante) Darstellung dieser:
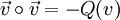 , wobei , wobei 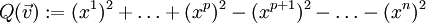
eine quadratische Funktion auf V ist, welche ein (Pseudo-)Skalarprodukt definiert:
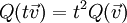 und und 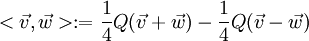 . .
Die Erzeugenden bilden dann eine Orthonormalbasis auf (V, ⟨, ⟩).
Ein solches Paar aus reellem Vektorraum und darauf definierter quadratischer Funktion (V,Q) ist der Ausgangspunkt für die mathematische Theorie der Clifford-Algebren.
Mathematische Definition
Es sei V ein 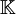 -Vektorraum. Eine Funktion -Vektorraum. Eine Funktion 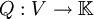 heißt quadratische Form, falls es eine zugeordnete symmetrische Bilinearform heißt quadratische Form, falls es eine zugeordnete symmetrische Bilinearform 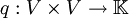 gibt mit Q(v)=q(v,v). gibt mit Q(v)=q(v,v).
In der Mathematik ist die Clifford-Algebra (nach William Kingdon Clifford) Cl(V,Q) eines reellen Vektorraums V mit quadratischer Form Q eine (Universalkonstruktion) assoziative Algebra,
- in welche V injektiv eingebettet ist – d.h. es gibt eine injektive Abbildung
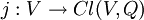 – und – und
- in welcher für das Produkt eingebetteter Vektoren gilt
- j(v)j(v)=-Q(v) für alle v aus V bzw. die äquivalente Aussage
- j(v)j(w)+j(w)j(v)=-2q(v,w) für alle v, w aus V,
- wobei
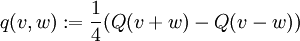 die von Q durch Polarisierung erhaltene symmetrische Bilinearform ist, die von Q durch Polarisierung erhaltene symmetrische Bilinearform ist,
die die universelle Eigenschaft erfüllt
- zu jeder weiteren Einbettung f:V → A gibt es einen eindeutigen Algebrenmorphismus φ:Cl(V,Q) → A mit f=φ∘j. Falls es eine solche Clifford-Algebra gibt, ist sie bis auf Isomorphie eindeutig.
Es sei im folgenden V mit seiner Einbettung j(V) identifiziert (d.h., wir lassen das j weg).
Konstruktion in der Tensoralgebra
In der Tensoralgebra 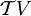 sei das Ideal sei das Ideal 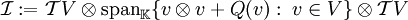 definiert. Dann ist der Quotient definiert. Dann ist der Quotient 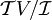 eine Realisierung der Clifford-Algebra Cl(V,Q). eine Realisierung der Clifford-Algebra Cl(V,Q).
Spezielle Clifford-Algebren
Falls V ein Spaltenvektorraum mit euklidischem Skalarprodukt ist, 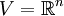 , so wird die Clifford-Algebra auch mit Cl(n,0) bezeichnet. Die Erzeugenden sind dann die kanonischen Basisvektoren , so wird die Clifford-Algebra auch mit Cl(n,0) bezeichnet. Die Erzeugenden sind dann die kanonischen Basisvektoren 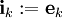 , die quadratische Form die Quadratsumme der Koordinaten. , die quadratische Form die Quadratsumme der Koordinaten.
Ist der Raum 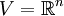 ein Minkowski-Raum der Signatur (p,q) mit Dimension n:=p+q, d.h. die quadratische Form ist gegeben durch ein Minkowski-Raum der Signatur (p,q) mit Dimension n:=p+q, d.h. die quadratische Form ist gegeben durch
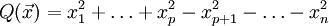 , ,
so wird die Clifford-Algebra auch mit 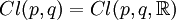 bezeichnet. bezeichnet.
Zu jeder Clifford-Algebra kann auch die komplexifizierte
Algebra 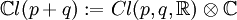 definiert werden,
hier sind alle Bilinearformen zueinander isomorph. definiert werden,
hier sind alle Bilinearformen zueinander isomorph.
Graduierung
Die Abbildung 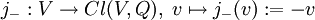 erfüllt ebenfalls die definierende Identität j − (v)2 = − Q(v), somit gibt es einen Algebrenisomorphismus erfüllt ebenfalls die definierende Identität j − (v)2 = − Q(v), somit gibt es einen Algebrenisomorphismus 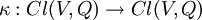 mit κ(v)=-v für alle v∈V und κ²=id. Damit zerfällt die Clifford-Algebra in einen geraden Teil Cl0(V,Q)=Kern(id-κ)=Bild(id+κ) und einen ungeraden Teil Cl1(V,Q)=Kern(id+κ)=Bild(id-κ). mit κ(v)=-v für alle v∈V und κ²=id. Damit zerfällt die Clifford-Algebra in einen geraden Teil Cl0(V,Q)=Kern(id-κ)=Bild(id+κ) und einen ungeraden Teil Cl1(V,Q)=Kern(id+κ)=Bild(id-κ).
Diese Zerlegung erzeugt eine 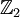 –Graduierung der Algebra, Produkte gerade-gerade und ungerade-ungerade ergeben gerade Elemente, Produkte gerade-ungerade ergeben ungerade Elemente. So sind Produkte mit einer geraden Anzahl von Faktoren aus V gerade, Produkte mit einer ungeraden Anzahl von Faktoren aus V ungerade –Graduierung der Algebra, Produkte gerade-gerade und ungerade-ungerade ergeben gerade Elemente, Produkte gerade-ungerade ergeben ungerade Elemente. So sind Produkte mit einer geraden Anzahl von Faktoren aus V gerade, Produkte mit einer ungeraden Anzahl von Faktoren aus V ungerade
Cl0(V,Q) ist eine Unteralgebra der Clifford-Algebra und wird auch als zweite Clifford-Algebra bezeichnet, Cl1(V,Q) ist ein lediglich ein Modul bezüglich Cl0(V,Q).
Beziehung zur Graßmann-Algebra
Die Graßmann–Algebra ΛV eines reellen Vektorraumes V ist die Clifford-Algebra Cl(V,0) mit der trivialen quadratischen Form Q≡0. Innerhalb einer beliebigen Clifford-Algebra kann die Graßmann-Algebra konstruiert werden, indem das Keilprodukt als u∧v:=½(uv-vu) – und analog als alternierende Summe bei mehr als zwei Faktoren – definiert wird.
Es kann umgekehrt jede Clifford-Algebra Cl(V,Q) innerhalb der Graßmann-Algebra ΛV konstruiert werden, indem in dieser ein neues Produkt ° definiert wird als
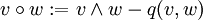 . .
Die Dimension der Algebra bleibt dabei erhalten, sie ist 2n bei n=dim(v).
Diese Beziehung ist u.a. für die Quantisierung supersymmetrischer Feldtheorien wichtig.
Beziehung zur orthogonalen Gruppe
Sei V ein Vektorraum mit nicht ausgearteter symmetrischer Bilinearform q und Q(v)=q(v,v). In der Clifford-Algebra Cl(V,Q) können dann Spiegelungen in V dargestellt werden. Dazu wird eine elementare Folgerung aus der Struktur des Produkts benutzt:
- vxv = − (2 < v,x > + xv)v = − 2 < v,x > v + x < v,v > .
Ist v ein Einheitsvektor, |⟨v,v⟩|=1, so ist die Abbildung v↦S(v)x:=vxv die Spiegelung an der zu v senkrechten Hyperebene. Jede Spiegelung ist eine orthogonale Abbildung, somit ist die von den Spiegelungen erzeugte Gruppe eine Untergruppe der orthogonalen Gruppe.
Die Pin-Gruppe
Umgekehrt lässt sich jede orthogonale Abbildung in ein Produkt aus Spiegelungen zerlegen, s. Householdertransformation bzw. QR-Zerlegung. Die Zerlegung ist nicht eindeutig, aber die Clifford-Produkte der Einheitsvektoren der Spiegelmatrizen unterscheiden sich höchstens im Vorzeichen. Betrachten wir solche Produkte.
Wir definieren zunächst die sog. "Pin"-Gruppe aller Produkte von Einheitsvektoren:
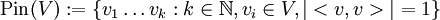 . .
Es gibt Produkte, deren Faktoren unterschiedlich sind, die aber das selbe Element der Pin-Gruppe bezeichnen, z.B. ist mit orthogonalen Einheitsvektoren v und w und jedem Paar (c,s)=(cosα, sinα) gilt
- (cv − sw)(sv + cw) = vw.
Jedoch gilt, dass jedem Element aus Pin(V) genau eine orthogonale Abbildung
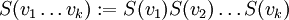
entspricht, unabhängig von der gewählten Faktorisierung. Weiter ist bekannt, dass
- S:Pin(V)->O(V) surjektiv der Ordnung 2 ist, d.h. eine zweifache Überlagerung. Die Urbilder der gleichen orthogonalen Abbildung unterscheiden sich nur um das Vorzeichen.
Die Spin-Gruppe
Physikalisch und geometrisch bedeutsam ist aber eine Untergruppe der Pin-Gruppe, die Spin-Gruppe
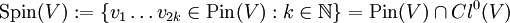
der Produkte mit gerader Anzahl von Faktoren (aus dem Wortspiel "spezielle Pin-Gruppe" ergab sich der Begriff "Pin"-Gruppe). Von dieser ist bekannt, dass sie ebenfalls eine zweifache Überlagerung der speziellen orthogonalen Gruppe SO(V) ist, sowie dass sie einfach zusammenhängend ist, d.h. selbst nur noch triviale Überlagerungen zulässt. Da die Matrixgruppe SO(n) eine Darstellung vom Gewicht 2 von Spin(n) ist, sagt man in der Physik auch, dass Darstellungen der Spin-Gruppe vom Gewicht 1 Spin-1/2-Darstellungen der orthogonalen Gruppe seien.
Darstellungen
Eine Darstellung einer Algebra ist eine Einbettung dieser in die Algebra der Endomorphismen eines Vektorraums, also (nach Basiswahl) in eine Matrixalgebra. Dabei können die Matrizen reelle, komplexe oder quaternionische Einträge haben.
Es lässt sich zeigen, dass jede Clifford-Algebra zu einer Matrixalgebra oder der direkten Summe zweier Matrix-Algebren über den reellen Zahlen  , den komplexen Zahlen , den komplexen Zahlen 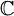 oder den Quaternionen oder den Quaternionen 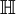 isomorph ist. Die Zuordnung und Dimension der reellen Algebren tabelliert sich wie folgt: isomorph ist. Die Zuordnung und Dimension der reellen Algebren tabelliert sich wie folgt:
| p−q mod 8 | ω2
| Cl(p,q,R)
(p+q = 2m)
| p−q mod 8 | ω2
| Cl(p,q,R)
(p+q = 2m + 1)
|
| 0 | + | R(2m)
| 1 | − | C(2m)
|
| 2 | − | H(2m−1)
| 3 | + | H(2m−1) ⊕ H(2m−1)
|
| 4 | + | H(2m−1)
| 5 | − | C(2m)
|
| 6 | − | R(2m)
| 7 | + | R(2m) ⊕ R(2m)
|
Im komplexifizierten Fall ergibt sich ein einfacheres Bild:
| n | Cl(n,C)
|
| 2m | C(2m)
|
| 2m+1 | C(2m) ⊕ C(2m)
|
Dabei gelten folgende allgemeinen Isomorphien:
Niedrigdimensionale Beispiele
Die Dimension von Cl(p,q) als reeller Vektorraum ist 2p+q. Damit lässt sich die Clifford-Algebra durch reelle Matrizen dieser Dimension darstellen, welche die Multiplikation in der Algebra beschreiben. Diese Darstellung ist nicht minimal, d.h. es gibt Matrizen geringerer Dimension, welche das gleiche leisten, siehe [1] und die Beispiele unten.
- hat den Generator e1 mit e12=-1. Es gibt also eine komplex eindimensionale Darstellung, welche e1 auf die imaginäre Einheit i abbildet, und die entsprechende reell zweidimensionale.
- Der Generator ist e1 mit e12=1. Jedes Element a+be der Algebra kann in zwei Summanden ½(a+b)(1+e) und ½(a-b)(1-e) aufgespalten werden. Da (1+e)(1-e)=0 gilt, erhält sich diese Aufspaltung unter Produktbildung. Die Clifford-Algebra ist also isomorph zum ℝ² mit gliedweisem Produkt, wobei e dem Element (1,-1) entspricht und (1,1) dem Einselement. Diese direkte Summe zweier Algebren kann auch als Algebra der 2x2-Diagonalmatrizen realisiert werden.
- Cl(2,0)≅
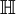
- hat die Generatoren i:=e1 und j:=e2 und deren Produkt k=ij mit den Relationen
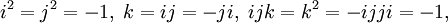 . .
- Man rechnet nach, dass dies zur Algebra der Quaternionen isomorph ist.
- hat die Generatoren i und e, i²=-1, e²=1 und ie=-ei. Man überzeugt sich, dass die Generatoren folgenden reellen 2x2-Matrizen entsprechen:
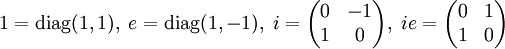
- somit alle reellen Matrizen erreicht werden.
- hat die Generatoren e1 und e2 mit Quadrat 1, deren Produkt i:=e1e2 hat das Quadrat -1, somit ist diese Algebra isomorph zur vorhergehenden.
Quantenphysikalisch bedeutsame Beispiele
- Cl(3,0)≅Cl(2,0)⊗Cl(0,1)≅
 (Biquaternionen) (Biquaternionen)
- hat die Generatoren e1, e2 und e3 mit den Relationen
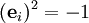 , , 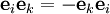 , , 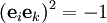 , , 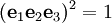 . .
- Sowohl reelle als auch komplexe Darstellungen zerfallen als V=V+⊕V-, wobei V+ Nullraum des Projektors (1-ω)/2, V- Nullraum des Projektors (1+ω)/2 mit ω:=e1e2e3 ist. Es gilt ekω=ωek, so dass beide Untervektorräume voneinander unabhängige Unterdarstellungen erzeugen.
- Eine rein negative Darstellung, d.h. mit V+={0}, ist direkt zur Quaternionen-Algebra isomorph,
- e1↦i, e2↦j und e3↦k,
- eine rein positive ist konjugiert isomporph,
- e1↦-i, e2↦-j und e3↦-k.
- In beiden Fällen gilt das zu
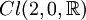 gesagte. gesagte.
- Cl(2,1)≅Cl(1,1)⊗Cl(1,0)≅M2(ℂ)
- Cl(1,2)≅Cl(1,1)⊗Cl(0,1)≅M2(ℝ)⊕M2(ℝ)
- Cl(0,3)≅Cl(0,2)⊗Cl(1,0)≅
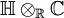
- Cl(4,0)≅Cl(2,0)⊗Cl(0,2)≅M2(ℍ)
- Der gerade Teil dieser Algebra, der die Spin4-Gruppe enthält, ist zu Cl(3,0) isomorph. Er wird erzeugt von
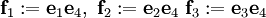 , es ist z.B. , es ist z.B. 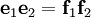 . .
- Cl(3,1)≅Cl(1,1)⊗Cl(2,0)≅M2(ℍ)
- Cl0(3,1)≅Cl(3,0)≅
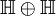 oder oder
- Cl0(3,1)≅Cl(2,1)≅M2(ℂ)
- Cl(1,3)≅Cl(1,1)⊗Cl(0,2)≅M4(ℝ)
- Cl0(1,3)≅Cl(0,3)≅
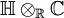 oder oder
- Cl0(1,3)≅Cl(1,2)≅M2(ℝ)⊕M2(ℝ)
Literatur
- Bartel L. van der Waerden, Algebra I, Spinger-Verlag, 9. Aufl. 1991, ISBN 3-540-56799-2
- Bartel L. van der Waerden, A history of Algebra, Springer-Verlag, 1985, ISBN 3-540-13610-X
- H.B. Lawson, M. Michelsohn, Spin Geometry, Princeton University Press, 1989, ISBN 978-0691085425, ISBN 0691085420
|





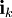 fixiert werden, welche mit der 1 zusammen den Zahlenraum als reellen Vektorraum aufspannen und welche (nicht nur)
fixiert werden, welche mit der 1 zusammen den Zahlenraum als reellen Vektorraum aufspannen und welche (nicht nur) 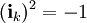 erfüllen. Manchmal reicht das nicht aus. Es werden zu einer beliebigen Anzahl n Strukturen gesucht, welche die reellen Zahlen und Elemente
erfüllen. Manchmal reicht das nicht aus. Es werden zu einer beliebigen Anzahl n Strukturen gesucht, welche die reellen Zahlen und Elemente 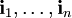 enthalten und in der ein Produkt ° definiert ist, welches die Bedingungen
enthalten und in der ein Produkt ° definiert ist, welches die Bedingungen
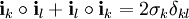
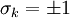 .
.
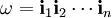 . Das Quadrat von
. Das Quadrat von 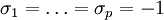 und
und 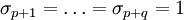
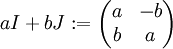 .
.
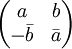 ,
,
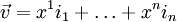 dieses Vektorraums, so ergibt sich eine koordinatenfreie (für Physiker: kovariante) Darstellung dieser:
dieses Vektorraums, so ergibt sich eine koordinatenfreie (für Physiker: kovariante) Darstellung dieser:
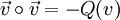 , wobei
, wobei 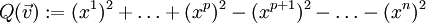
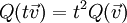 und
und 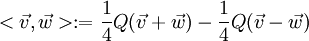 .
.
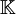 -Vektorraum. Eine Funktion
-Vektorraum. Eine Funktion 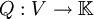 heißt quadratische Form, falls es eine zugeordnete symmetrische Bilinearform
heißt quadratische Form, falls es eine zugeordnete symmetrische Bilinearform 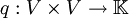 gibt mit Q(v)=q(v,v).
gibt mit Q(v)=q(v,v).
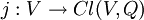 – und
– und
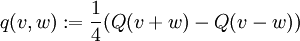 die von Q durch Polarisierung erhaltene symmetrische Bilinearform ist,
die von Q durch Polarisierung erhaltene symmetrische Bilinearform ist,
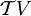 sei das Ideal
sei das Ideal 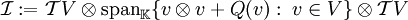 definiert. Dann ist der Quotient
definiert. Dann ist der Quotient 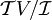 eine Realisierung der Clifford-Algebra
eine Realisierung der Clifford-Algebra  , so wird die Clifford-Algebra auch mit
, so wird die Clifford-Algebra auch mit 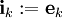 , die quadratische Form die Quadratsumme der Koordinaten.
, die quadratische Form die Quadratsumme der Koordinaten.
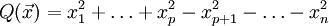 ,
,
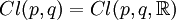 bezeichnet.
bezeichnet.
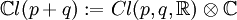 definiert werden,
hier sind alle Bilinearformen zueinander isomorph.
definiert werden,
hier sind alle Bilinearformen zueinander isomorph.
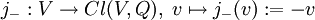 erfüllt ebenfalls die definierende Identität
erfüllt ebenfalls die definierende Identität 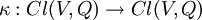 mit κ(v)=-v für alle v∈V und κ²=id. Damit zerfällt die Clifford-Algebra in einen geraden Teil Cl0(V,Q)=Kern(id-κ)=Bild(id+κ) und einen ungeraden Teil Cl1(V,Q)=Kern(id+κ)=Bild(id-κ).
mit κ(v)=-v für alle v∈V und κ²=id. Damit zerfällt die Clifford-Algebra in einen geraden Teil Cl0(V,Q)=Kern(id-κ)=Bild(id+κ) und einen ungeraden Teil Cl1(V,Q)=Kern(id+κ)=Bild(id-κ).
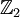 –Graduierung der Algebra, Produkte gerade-gerade und ungerade-ungerade ergeben gerade Elemente, Produkte gerade-ungerade ergeben ungerade Elemente. So sind Produkte mit einer geraden Anzahl von Faktoren aus V gerade, Produkte mit einer ungeraden Anzahl von Faktoren aus V ungerade
–Graduierung der Algebra, Produkte gerade-gerade und ungerade-ungerade ergeben gerade Elemente, Produkte gerade-ungerade ergeben ungerade Elemente. So sind Produkte mit einer geraden Anzahl von Faktoren aus V gerade, Produkte mit einer ungeraden Anzahl von Faktoren aus V ungerade
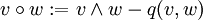 .
.
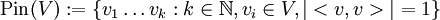 .
.
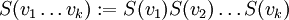
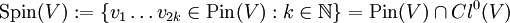
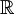 , den komplexen Zahlen
, den komplexen Zahlen 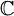 oder den Quaternionen
oder den Quaternionen 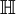 isomorph ist. Die Zuordnung und Dimension der reellen Algebren tabelliert sich wie folgt:
isomorph ist. Die Zuordnung und Dimension der reellen Algebren tabelliert sich wie folgt:
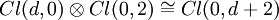
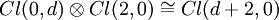
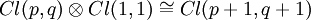
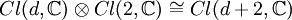
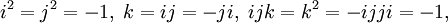 .
.
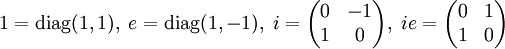
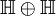 (Biquaternionen)
(Biquaternionen)
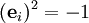 ,
, 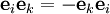 ,
, 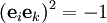 ,
, 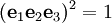 .
.
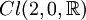 gesagte.
gesagte.
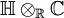
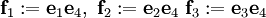 , es ist z.B.
, es ist z.B. 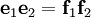 .
.


