Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Dirac-TheorieDie Dirac-Theorie ist ein Teil der Quantenmechanik, der auch die spezielle Relativitätstheorie mit einbezieht. Sie wurde 1928 von Paul A. M. Dirac ausgehend von der Klein-Gordon-Gleichung entwickelt.
Die Dirac-Theorie beschreibt die Eigenschaften und das Verhalten von Teilchen mit Spin 1/2 – also der Fermionen und deren Antiteilchen. Die Klein-Gordon-Gleichung beschreibt dagegen das Verhalten von Teilchen mit Spin 0, also der sogenannten Spin-0-Bosonen. Auf Teilchen mit Spin Die wichtigsten Erfolge der Dirac-Theorie sind:
Produkt-Highlight
Freie Dirac-GleichungGrundlage der Dirac-Theorie ist die Dirac-Gleichung. Dabei handelt es sich um eine Differentialgleichung für einen Spinor ψ, der im Allgemeinen als vierkomponentige Wellenfunktion geschrieben wird. Die Anzahl der Komponenten wird durch die zwei möglichen Zustände des Spins und die zwei möglichen Vorzeichen der Energieeigenwerte erklärt. SchrödingerformDie Dirac-Gleichung für ein kräftefreies Teilchen der Masse m lautet in der Schrödingerform
Dabei ist Diese Matrizen lassen sich kompakter mit Hilfe der Pauli-Matrizen schreiben: Diese Form der Dirac-Gleichung heißt auch Dirac-Darstellung. Neben der Dirac-Darstellung gibt es noch andere mögliche Darstellungen, wie z.B. die Weyl- oder Majorana-Darstellung , die jedoch alle dieselben physikalischen Ergebnisse liefern. Der Hamiltonoperator der freien Dirac-Gleichung
wobei E die möglichen Energien des Teilchens sind. Diese Gleichung kann sowohl für positive als auch für negative E, genauer für Kovariante SchreibweiseEine besonders elegante Schreibweise lässt sich durch die Einführung von Dirac-Matrizen γμ erzielen: Nach dem ersten Gleichheitszeichen wurde hierbei die Feynmansche Slash-Schreibweise Sonstiges zur freien Dirac-GleichungFür jede Komponente ψα kann die Dirac-Gleichung als Quadratwurzel der Klein-Gordon-Gleichung aufgefasst werden. Wendet man den komplex-konjugierten Dirac-Operator Die elektromagnetische WechselwirkungMinimale KopplungIn der Quantenmechanik wird die Anwesenheit eines elektromagnetischen Feldes durch die folgenden Substitutionen des Impuls- und Zeitentwicklungsoperators in der Schrödingergleichung berücksichtigt:
Dabei ist e die elektrische Ladung des Teilchens, Damit ergibt sich die Diracgleichung für ein Teilchen im elektromagnetischen Feld: Führt man mit dieser Gleichung einige Näherungen durch (Details), erhält man die Pauli-Gleichung, die das Verhalten eines nicht-relativistischen Spin-½-Teilchens im elektromagnetischen Feld beschreibt. Auf diese Weise kann das Stern-Gerlach-Experiment (Spinorientierung von Silberatomen im inhomogenen Magnetfeld - 1921) erklärt werden. In der kovarianten Formulierung der Elektrodynamik werden die beiden Potenziale hergestellt werden. Landé-FaktorFür mehr Informationen siehe Landé-Faktor Ein geladenes Teilchen der Masse m mit der Ladung e hat ein magnetisches Moment Auch der Spin Der Faktor g wird Landé-Faktor (auch g-Faktor oder gyromagnetisches Moment) genannt. Er gibt die relative Stärke des von Bahndrehimpuls und Spin erzeugten magnetischen Moments an. Der Landé-Faktor eines Elektrons beträgt g = 2. Diese Tatsache kann in der nicht-relativistischen Quantenmechanik nicht erklärt werden und muss als Annahme in die Pauli-Gleichung gesteckt werden. Bei der Ableitung der Pauli-Gleichung als nicht-relativistischer Grenzfall der Dirac-Gleichung kommt dieser Faktor jedoch automatisch richtig heraus. Präzisionsmessung zeigen, dass der wahre g-Faktor des Elektrons von 2 abweicht und in Wahrheit ungefähr g = 2,0023 beträgt. Diese Abweichung kann im Rahmen der Quantenelektrodynamik als Ergebnis der Wechselwirkung des Elektrons mit seinem eigenen Strahlungsfeld verstanden und mit großer Genauigkeit theoretisch vorhergesagt werden. Quellen
Artikel
Bücher
|
|
| Dieser Artikel basiert auf dem Artikel Dirac-Theorie aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


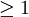 kann zwar keine der beiden Gleichungen direkt angewandt werden, allerdings lassen sich unter Verwendung geeigneter Multispinoren
kann zwar keine der beiden Gleichungen direkt angewandt werden, allerdings lassen sich unter Verwendung geeigneter Multispinoren 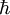 annehmen kann, beträgt er für den intrinsischen Drehimpuls des Elektrons
annehmen kann, beträgt er für den intrinsischen Drehimpuls des Elektrons 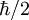 . Damit in Zusammenhang steht auch
. Damit in Zusammenhang steht auch



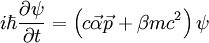 .
.
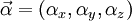 ein Vektor aus
ein Vektor aus 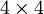 -Matrizen und
-Matrizen und 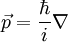 der
der 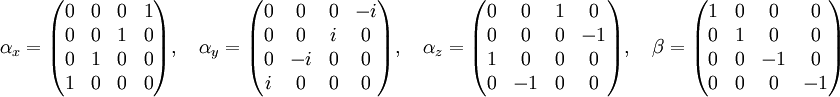
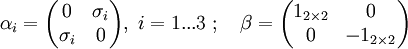
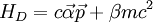 wird manchmal auch freier Diracoperator genannt und mit
wird manchmal auch freier Diracoperator genannt und mit ![E\in (-\infty,-mc^2]\cup[mc^2,\infty)](images/math/c/7/8/c78babb8516ab518dd51c59d8d176f75.png) erfüllt werden. Das Auftreten von negativen Energieeigenwerten war hier zunächst verblüffend. Eine Erklärung dafür gibt Dirac mit seiner Theorie vom
erfüllt werden. Das Auftreten von negativen Energieeigenwerten war hier zunächst verblüffend. Eine Erklärung dafür gibt Dirac mit seiner Theorie vom 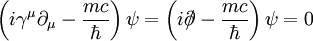
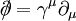 verwendet, wobei entsprechend der Einsteinschen Summenkonvention über die
verwendet, wobei entsprechend der Einsteinschen Summenkonvention über die 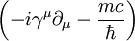 auf die Dirac-Gleichung an, so entsteht für jede Komponente
auf die Dirac-Gleichung an, so entsteht für jede Komponente 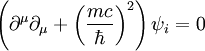
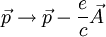 ;
;
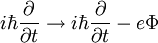
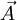 das
das 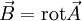 und
und 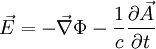 .
.
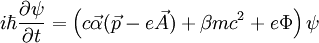
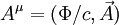 zusammengefasst. Dann kann die minimale Kopplung durch den Übergang
zusammengefasst. Dann kann die minimale Kopplung durch den Übergang
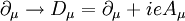
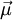 , das im wesentlichen das Verhalten des Teilchens in einem Magnetfeld bestimmt. Ein magnetisches Moment kann zum Beispiel durch den Bahndrehimpuls
, das im wesentlichen das Verhalten des Teilchens in einem Magnetfeld bestimmt. Ein magnetisches Moment kann zum Beispiel durch den Bahndrehimpuls 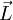 des Teilchens erzeugt werden:
des Teilchens erzeugt werden:
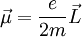
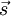 eines Teilchens trägt zum magnetischen Moment bei:
eines Teilchens trägt zum magnetischen Moment bei: