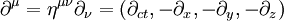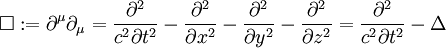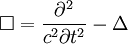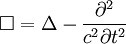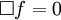Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
D’AlembertoperatorDer d’Alembert-Operator Produkt-Highlight
DefinitionIm Rahmen der speziellen Relativitätstheorie (SRT) wird der Vierergradient durch
definiert. Die kontravarianten Komponenten ergeben sich durch Heraufziehen des kovarianten Index mit: Durch Kombination der beiden Operatoren lässt sich der lorentzinvariante d’Alembert-Operator bilden: Er enthält nur zweite Ableitungen. VorzeichenkonventionenWie in der SRT üblich sind die Vorzeichen von der Signatur der Metrik abhängig. Oft wird in der SRT die Konvention (+,−,−,−) für die Signatur der Minkowski-Metrik verwendet, ansonsten benutzt man die Konvention (−,+,+,+). Für die erste Signatur ergibt sich der d’Alembert-Operator, wie oben bereits gezeigt, zu: Für die andere Signatur ergibt sich analog: WellengleichungUrsprünglich kommt der d'Alembert-Operator aus der Elektrodynamik und ergibt sich bei der Herleitung der Wellengleichung. Hieran ist deutlich zu erkennen, dass es sich bei der Elektrodynamik bereits um eine relativistische Theorie handelte, noch ehe man die SRT kannte. Zudem ist der d'Alembert-Operator ein Lorentz-Skalar und somit invariant unter Lorentz-Transformationen. Er spielt damit auch eine wichtige Rolle in der relativistischen Elektrodynamik. Unter Verwendung des d'Alembert-Operators kann für eine zweimal differenzierbare Funktion f(x,t) die Wellengleichung in einer sehr kompakten Form geschrieben werden Literatur
|
|
| Dieser Artikel basiert auf dem Artikel D’Alembertoperator aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


 (nach Jean Baptiste le Rond d’Alembert) ist ein Differentialoperator, der sich aus der Verallgemeinerung des Gradienten im vierdimensionalen Minkowskiraum ergibt. Er wird auch Quabla, Viereckoperator oder Wellenoperator genannt.
(nach Jean Baptiste le Rond d’Alembert) ist ein Differentialoperator, der sich aus der Verallgemeinerung des Gradienten im vierdimensionalen Minkowskiraum ergibt. Er wird auch Quabla, Viereckoperator oder Wellenoperator genannt.

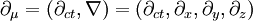 .
.