Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Ehrenfest-TheoremDas Ehrenfest-Theorem, benannt nach dem österreichischen Physiker Paul Ehrenfest, stellt innerhalb der Physik einen Zusammenhang zwischen der klassischen Mechanik und der Quantenmechanik her. Es besagt, dass unter bestimmten Bedingungen die klassischen Bewegungsgleichungen für die Mittelwerte der Quantenmechanik gelten; die klassische Mechanik also in gewissem Maße in der Quantenmechanik enthalten ist (Korrespondenzprinzip). Mathematisch drückt sich das in seiner allgemeinsten Form so aus, dass die vollständige Zeitableitung des Erwartungswertes eines quantenmechanischen Operators mit dem Kommutator dieses Operators und des Hamiltonoperators wie folgt in Zusammenhang stehen: Dabei stellt O einen quantenmechanischen Operator und Produkt-Highlight
AnwendungIm Hamilton-Formalismus der klassischen Mechanik gilt für die Zeitentwicklung einer Phasenraumfunktion:
mit der Poisson-Klammer Für den Spezialfall des nicht explizit zeitabhängigen Impulsoperators p gilt somit: Da weiterhin für die Zeitentwicklung des Ortsoperators folgt lässt sich folgern: Lässt sich nun der Erwartungswert der Funktion F der Position x durch die Funktion F des Erwartungswerts der Position x nähern, so erhält man und somit
In Worten bedeutet dies, dass sich das Maximum der Aufenthaltswahrscheinlichkeit auf einer klassischen Bahn bewegt, d.h. der klassischen Bewegungsgleichung folgt. Das Ehrenfest-Theorem führt somit direkt auf eine Analogie der Quantenmechanik zur klassischen Mechanik - hier in Form des zweiten Newton'schen Axioms
Die Annahme (*) und damit auch die klassische Bewegungsgleichung für quantenmechanische Erwartungswerte gelten allerdings nur, falls die Kraft F(x) eine lineare Funktion der Position x ist. Dies gilt für die einfachen Fälle des harmonischen Oszillators oder des freien Teilchens. Außerdem kann man sagen, dass (*) gilt, wenn die Breite der Aufenthaltswahrscheinlichkeit klein ist gegenüber der typischen Längenskala auf der die Kraft F(x) variiert. HerleitungEs sei das betrachtete System im Quantenzustand Ψ. Man erhält somit für die Zeitableitung des Erwartungswertes eines Operators O:
Man betrachtet nun die Schrödingergleichung
Im zweiten Schritt wurde mit H = H * ausgenutzt, dass der Hamilton-Operator selbstadjungiert ist. Einsetzen dieser Relationen liefert nun:
Siehe auch
Literatur
|
|
| Dieser Artikel basiert auf dem Artikel Ehrenfest-Theorem aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


![\frac{d}{dt}\langle O\rangle = \frac{i}{\hbar}\langle [H,O] \rangle + \left\langle \frac{\partial O}{\partial t}\right\rangle](images/math/2/7/3/2733bfe4850d0cd787b22dadfb3c0a31.png)
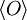 dessen Erwartungswert dar.
dessen Erwartungswert dar.



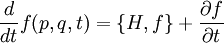
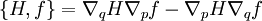 . Bei der Quantisierung wird die Poisson-Klammer durch den mit
. Bei der Quantisierung wird die Poisson-Klammer durch den mit 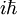 multiplizierten Kommutator ersetzt. Das quantenmechanische Analogon einer Phasenraumfunktion ist ein Operator (
multiplizierten Kommutator ersetzt. Das quantenmechanische Analogon einer Phasenraumfunktion ist ein Operator (![\frac{d}{dt} \langle p \rangle = \frac{i}{\hbar} \langle [H,p] \rangle = \frac{i}{\hbar} \langle [V,p]\rangle = \frac{i}{\hbar} \langle -\frac{\hbar}{i} \nabla V \rangle = - \langle \nabla V \rangle](images/math/a/7/3/a73290ae1b676171399c9a557f40eeef.png)
![\frac{d}{dt}\langle x\rangle = \frac{i}{\hbar}\langle[H,x]\rangle =\frac{1}{m}\langle p\rangle](images/math/8/a/1/8a1b2adeca30f43afaa2ef2d1c10a77a.png)
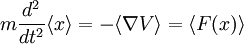
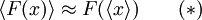
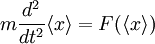 .
.
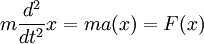 .
.
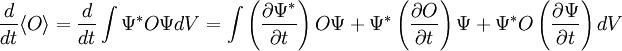
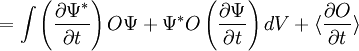
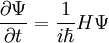
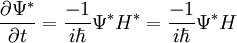
![\frac{d}{dt}\langle O\rangle = \frac{1}{i\hbar}\int -\Psi^* HO \Psi + \Psi^* OH\Psi dV + \langle\frac{\partial O}{\partial t}\rangle=\frac{1}{i\hbar}\langle[O,H]\rangle + \langle \frac{\partial O}{\partial t}\rangle = \frac{i}{\hbar}\langle[H,O]\rangle + \langle \frac{\partial O}{\partial t}\rangle](images/math/4/0/2/4022888b7e64ad2a8e6c2c8525c20733.png)


