Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Harmonischer Oszillator
Der harmonische Oszillator ist in der klassischen Mechanik ein System, welches ein bei einer Auslenkung x aus der Ruhelage eine der Auslenkung proportionale Rückstellkraft erfährt
wobei k die Federkonstante des Oszillators ist. Das Standardbeispiel eines solchen Systems ist etwa eine schwingende Spiralfeder. Produkt-Highlight
RealisierbarkeitDa es in der Natur keine reibungsfreien Abläufe gibt, existiert ein perfekter, ungedämpfter harmonischer Oszillator nicht. Dennoch ist das Konzept für die Physik von fundamentaler Bedeutung, da in vielen physikalischen Modellen nur kleine Auslenkungen eines Objekts aus der Ruhelage betrachtet werden. Beschränkt man sich darauf, so kann das Potential des betrachteten Systems in der Regel gut mit einem harmonischen Oszillator beschrieben werden. Der Vorteil einer solchen Näherung besteht darin, dass das Problem mit Standardmethoden handhabbar wird und einfach zu interpretierende analytische Lösungen erhalten. Federpendel und Fadenpendel bei kleinen Auslenkungen sind Beispiele für harmonische Oszillatoren in der Mechanik. Der elektrische Schwingkreis ist ein Beispiel aus der Elektrizitätslehre. Mathematische BeschreibungDie Differentialgleichung des ungedämpften harmonischen Oszillators, wird üblicherweise umgeschrieben zu wobei Zur Verallgemeinerung kann der Rückstellkraft noch ein Dämpfungsterm Wenn die von außen auf das System einwirkende Kraft ebenfalls periodisch ist, also in Schwingungen übertragen wird, so kann sie dem Oszillator Energie hinzufügen oder entziehen, je nach Phasenlage. Mit jedem Kraftübertrag wird dann etwas Energie zur Schwingung hinzugefügt oder entfernt, so dass die Amplitude anwächst oder abnimmt. Bei einem schwach gedämpften System kann dies zur sogenannten Resonanzkatastrophe führen, einem extremen Anstieg der Amplitude, welcher das System zerstören kann. Der Oszillator in mehreren DimensionenEin harmonischer Oszillator in n Dimensionen hat das Potential und das Kraftgesetz Da die Kraftkomponenete in einer Dimension nur von der Auslenkung in dieser Dimension abhängt, sind die Lösungen für die einzelnen Komponenten des Ortsvektors die Lösungen des entsprechenden eindimensionalen Problems. QuantenmechanikSiehe Hauptartikel: Harmonischer Oszillator (Quantenmechanik) Anharmonischer OszillatorBeim anharmonischen Oszillator treten mehr oder minder große Abweichungen vom linearen Kraftgesetz bzw. vom quadratischen Potential auf. Ist das System stark gedämpft und die Anharmonizität klein, so macht sie sich in der Regel nur dadurch bemerkbar, dass Oberschwingungen der Grundfrequenz auftreten. Wenn das System nur schwach gedämpft ist oder der nichtlineare Term das Kraftgesetz dominiert, so kann chaotisches Verhalten auftreten. Beispiele dafür sind der Toda-Oszillator und der Duffing-Oszillator. Kategorien: Physikalische Chemie | Spektroskopie | Theoretische Chemie |
|
| Dieser Artikel basiert auf dem Artikel Harmonischer_Oszillator aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


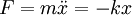 ,
,



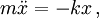
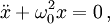
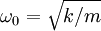 die Kreisfrequenz des Oszillators ist.
die Kreisfrequenz des Oszillators ist.
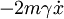 , welcher zur Geschwindigkeit
, welcher zur Geschwindigkeit 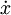 proportional und entgegengesetz ausgerichtet ist, sowie eine antreibende Kraft
proportional und entgegengesetz ausgerichtet ist, sowie eine antreibende Kraft