Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
SchrödingergleichungDie Schrödingergleichung ist eine, bzw. die, zentrale Grundgleichung der nichtrelativistischen Quantenmechanik. Die Lösungen dieser Gleichung werden auch Wellenfunktionen genannt. Diese Wellenfunktionen beschreiben die räumliche und zeitliche Entwicklung des Zustands eines Quantensystems. Die Gleichung wurde 1926 von Erwin Schrödinger (1887-1961) zuerst als Wellengleichung aufgestellt. Als „Bewegungsgleichung der Quantenmechanik“ bildet sie noch heute das Fundament für fast alle praktischen Anwendungen der Quantenmechanik. Produkt-HighlightEinführungDie komplexwertige Wellenfunktion
wobei m die Masse des Teilchens, Wenn das Potential nicht von der Wellenfunktion abhängt, was in den meisten Anwendungsfällen gilt, ist die Schrödingergleichung linear, so dass das Superpositionsprinzip für die Lösungen gilt: Wenn ψ1 und ψ2 Lösungen sind, so ist auch Mit dem Hamilton-Operator lässt sich die Schrödingergleichung in ihrer allgemeinen Form schreiben. Heuristische HerleitungDie Schrödingergleichung ist, wie die Newtonschen Axiome in der klassischen Physik, ein Postulat und lässt sich deshalb auch nicht mathematisch streng herleiten. Vielmehr wurde die Gleichung 1926 von Schrödinger, unter Berücksichtigung gewisser physikalischer Prinzipien und gestützt auf die bereits zu seiner Zeit bekannten quantenmechanischen Phänomene als neue Theorie postuliert. Manche Autoren heben hier auch die starke Anlehnung an die Prinzipien der Optik hervor. Mathematisch gesehen entsteht die Schrödingergleichung in der Ortsdarstellung nach dem Korrespondenzprinzip aus der Hamiltonfunktion (Ausdruck für die Energie) des betrachteten Problems durch Ersetzen der klassischen Größen Energie, Impuls und Ort durch die entsprechenden quantenmechanischen Operatoren (Korrespondenzprinzip): Anschließendes Anwenden auf die unbekannte Wellenfunktion
Auf die gleiche Weise kann die Hamiltonfunktion in einen Hamilton-Operator umgewandelt werden. Historisch gesehen ging Schrödinger von Louis de Broglie´s Beschreibung freier Teilchen aus und führte in seiner Arbeit Analogien zwischen Atomphysik und elektromagnetischen Wellen, in Form von De-Broglie-Wellen, ein:
wobei A eine Konstante ist. Diese Wellenfunktion ist eine Lösung der eben genannten Schrödingergleichung mit Eine völlig andere Möglichkeit, die Schrödingergleichung aufzustellen, benutzt den von dem US-amerikanischen Physiker und Nobelpreisträger R.P. Feynman eingeführten Begriff des Pfadintegrals. Diese alternative Herleitung betrachtet die Wahrscheinlichkeiten für die verschiedenen Bewegungen (Pfade) des zu untersuchenden Teilchens von einem Ort A nach B und kommt damit wieder zu genau der gleichen Schrödingergleichung.
Normierung der WellenfunktionFür die statistische Interpretation der Quantenmechanik ist es notwendig die Lösungen der Schrödingergleichung so zu normieren, dass ist. Diese sogenannte Normierungsbedingung sagt aus, dass die Wahrscheinlichkeit, dass das Teilchen irgendwo im gesamten Raum zu finden ist, 100% beträgt. Für die so erhaltenen normierten Lösungen entspricht dann Aus der Tatsache dass die Schrödinger-Gleichung invariant ist unter der Phasentransformation Erwartungswerte von MessgrößenAus der so gefundenen Wellenfunktion ergeben sich nun alle gesuchten, physikalischen Eigenschaften des Teilchens. Beispielsweise wird der klassische Wert für den Ort des Teilchens ersetzt, während der klassische Wert für den Impuls des Teilchens durch folgenden Mittelwert ersetzt wird:
Im Prinzip wird also jede klassische Messgröße f(r,p,t) durch eine Mittelung des zugehörigen Operators über den Raum, in dem sich das Teilchen befindet, ersetzt:
Der Ausdruck ErläuterungenWährend die Bahn eines klassisches Teilchens genau festgelegt ist, erscheint in der Quantenmechanik der Ort eines Teilchens nur noch als Erwartungswert mit Verteilungsfunktionen ψ, die durch die Schrödingergleichung gegeben sind. Es wird deswegen gerne auch anschaulich davon gesprochen, dass das Teilchen über den Raum delokalisiert sei. Ist die Breite des Wellenpakets, das das Teilchen beschreibt, genügend klein, kann mit Hilfe der Schrödingergleichung die Newtonsche Bewegungsgleichung als Grenzfall hergeleitet werden. Das gleiche Resultat ergibt sich auch durch die Limesbildung Die oben angegebene Schrödingergleichung ist diejenige in der sogenannten Ortsdarstellung. In der von einer bestimmten Darstellung unabhängigen Form lautet die Schrödingergleichung mit dem „ket“-Vektor
wobei hier die Operatoren und die Wahrscheinlichkeitserhaltung (Erhaltung der Norm des Zustands) drückt sich durch die Unitarität des Zeitentwicklungsoperators U aus, was wiederum darauf beruht, das H selbstadjungiert ist und damit nur reelle Eigenwerte besitzt. Dies ist im Übrigen eine Forderung, die an alle Operatoren gestellt wird, die nach dem Korrespondenzprinzip Messergebnisse repräsentieren. Da Messergebnisse stets als reel angenommen werden, kommen als zugeordnete Operatoren also nur hermitesche, bzw. selbstadjungierte Operatoren in Frage. Operatoren, die selbstadjungiert sind und Messergebnisse repräsentieren werden auch Observable genannt. In der Schrödingergleichung kommen die Wellenfunktion und die Operatoren im sogenannten Schrödinger-Bild vor. Im Heisenberg-Bild werden stattdessen Bewegungsgleichungen für die Operatoren selbst betrachtet. Diese Bewegungsgleichungen werden dann auch als Heisenbergsche Bewegungsgleichung bezeichnet. Beide Gleichungen sind physikalisch gleichwertig. Die Schrödingergleichung ist einerseits deterministisch, das heißt, dass die Lösungen bei Vorgabe von genügend Anfangs- und Randwertbedingungen genau bestimmt sind. Andererseits ist deren Lösung ψ jedoch nach der Kopenhagener Deutung eine statistische Größe und macht folglich auch nur Aussagen über die Mittelwerte von Messergebnissen in gleichartigen Versuchsanordnungen. Nach der Kopenhagener Deutung der Quantenmechanik liegt dies nicht an einem Mangel der Messanordnung oder des Experimentators, sondern ist durch die Physik und die Natur der atomaren Teilchen selbst bedingt. Mit der Formulierung der Schrödingergleichung wurde die ad hoc Konstruktion des Bohrschen Atommodells überwunden. Die dort nur postulierten diskreten Energieniveaus der Elektronen in Atomen ergeben sich hier aus der Lösung einer partiellen Differentialgleichung und zwar der bereits genannten Schrödingergleichung mit Lösung der SchrödingergleichungDie Lösungen der Schrödingergleichung werden zwar normalerweise als Wellenfunktion bezeichnet, haben aber nicht immer Ähnlichkeit mit einer klassischen Wellenfunktion. Deshalb sollen im Folgenden die Lösungen noch genauer vorgestellt werden.
mit dem reellen Parameter E, der hier für die Energie des stationären Zustandes steht, gelangt man sofort zu der folgenden zeitunabhängigen Schrödingergleichung:
Zusammen mit den Randbedingungen an ψ(r) bildet die zeitunabhängige Schrödingergleichung eine sogenannte Eigenwertaufgabe, bei der die Energieeigenwerte E und die zugehörigen Eigenfunktionen ψ(r) zu bestimmen sind. Ein einfaches Beispiel solch einer Eigenwertaufgabe bildet ein Elektron in einem Kasten ohne Potential und undurchdringlichen Rändern . Wie im eben gezeigten Falle der Zeitkoordinate kann häufig nach Wahl eines geeigneten Koordinatensystems auch für die Ortskoordinaten ein Separationsansatz gefunden werden. Die Schrödingergleichung reduziert sich dann von einer partiellen auf eine gewöhnliche Differentialgleichung zweiter Ordnung. Der Vektorraum der Lösungen dieser gewöhnlichen Differentialgleichung zweiter Ordnung wird von zwei linear unabhängigen Fundamentallösungen aufgespannt. Insbesondere gilt das für Probleme mit Kugelsymmetrie (symmetrisch unter Drehungen um einen Punkt) und Zylindersymmetrie (symmetrisch unter Drehungen um eine Achse). Die Schrödingergleichung lässt sich für einige einfache Potentiale exakt lösen, z. B.:
Bei komplizierteren Potentialen ist eine exakte Lösung meist nicht mehr möglich und es wird eine Form der Störungstheorie angewandt. Das heißt man unterteilt, wenn möglich, den Hamiltonoperator der Schrödingergleichung in einen Teil Eine einfache Möglichkeit Näherungslösungen der stationären Schrödingergleichung in Bereichen zu finden, in denen sich das Potential über die mittlere Wellenlänge des Teilchens nur wenig ändert, ist die WKB-Näherung. Bei Systemen mit mehreren Teilchen in einem Potential oder allgemein bei mehreren (untereinander wechselwirkenden) Teilchen muss die Schrödingergleichung vereinfacht (z.B. Born-Oppenheimer-Näherung in der Molekülphysik) oder approximativ gelöst werden. Ist trotz der Vereinfachung eine analytische Lösung immer noch unmöglich, wie z. B. bei den meisten Atomen und allen Molekülen, so müssen z.B. iterative Näherungsverfahren oder andere numerische Verfahren verwendet werden. Im Vielteilchenfall (z.B. im Bereich der Theoretischen Chemie) werden hierfür oft die Hartree-Fock-Methode und ihre Erweiterungen verwendet. Lagrangedichte der SchrödingergleichungDie Lagrangedichte der Schrödingergleichung lautet mit Schrödingergleichung für geladene Teilchen im elektromagnetischen FeldFalls das Teilchen, wie im Falle eines Elektrons oder Protons, eine elektrische Ladung besitzt, so verallgemeinert sich bei Anwesenheit eines äußeren elektromagnetischen Feldes der Hamiltonoperator in der Orts-Darstellung zu
wobei hier q die elektrische Ladung des Teilchens (q = -e bei Elektronen), c die Lichtgeschwindigkeit im Vakuum,
Meist wird die Bewegung geladener Teilchen in äußeren (vorgegebenen) elektromagnetische Feldern ( Schrödingergleichung in der MathematikAußerhalb der Physik genießt die Schrödingergleichung in der Mathematik ein hohes Maß an Interesse. Eine große Zahl von Mathematikern beschäftigt sich auch aktuell mit der Untersuchung von Existenz- und Eindeutigkeitsfragen, qualitativer Untersuchungen der Eigenschaften von speziellen Lösungen der Gleichungen (z. B. dem Untersuchen von Solitonen der Nichtlinearen Schrödingergleichung) und der numerischen Lösung der Gleichungen. Form der GleichungDie Natur ist für einen Mathematiker nicht unbedingt von solcher Bedeutung wie für einen Physiker. Daher werden die Konstanten weggelassen, die Schreibweise wird teilweise abstrahiert. Die Schrödingergleichung als Cauchyproblem hat folgende Gestalt:
Dabei wurde die explizite Abhängigkeit der Lösungsfunktion u von Zeit und Ort weggelassen. Wie das Vorkommen der Lösung u im Potentialterm f(u) schon andeutet ist hier auch die nichtlineare Schrödingergleichung ein bevorzugtes Untersuchungsobjekt. Passende RäumeZur Behandlung der Schrödingergleichung werden einheitlich die Sobolevräume gewählt. Wir bezeichnen hierbei für
wobei S' der Dualraum der Schwartzfunktionen, Eigenschaften von LösungenErhaltung der Hs-NormenEinfach zu sehen durch Fouriertransformation der Semigruppe. Dies drückt die Erhaltung der Wahrscheinlichkeiten aus.
DispersionEs gilt
Diese Eigenschaft drückt das Zerfließen der Wellenpakete aus. Mathematisch ist die Schrödingergleichung mit der Wärmeleitungsgleichung verwandt. AusblickDie Wechselwirkung des Spins oder Eigendrehimpulses des Teilchens mit einem äußeren Magnetfeld wird in obiger Form der Schrödingergleichung nicht berücksichtigt. Falls diese Wechselwirkung nicht vernachlässigt werden soll, ist für ein Elektron bei Anwesenheit eines äußeren Magnetfeldes die Pauli-Gleichung zu benutzen. Leider hat jedoch auch die Pauli-Gleichung noch einige grundlegende Mängel. Sie ist beispielsweise nicht lorentzinvariant sondern 'nur' galilei-invariant. Die korrekte relativistische Verallgemeinerung der Schrödinger- und auch der allgemeineren Pauli-Gleichung stellt für Elektronen die lorentzinvariante Diracgleichung dar, die im Gegensatz zur Schrödingergleichung eine partielle Differentialgleichung 1. Ordnung ist.
Kategorien: Quantenphysik | Theoretische Chemie |
| Dieser Artikel basiert auf dem Artikel Schrödingergleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





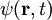 eines Punktteilchens in einem Potential
eines Punktteilchens in einem Potential 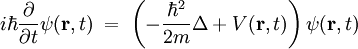 ,
,
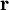 sein Ort,
sein Ort, 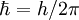 , sprich „h-quer“, ist das
, sprich „h-quer“, ist das 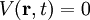 .
.
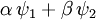 eine Lösung, wobei
eine Lösung, wobei 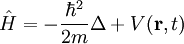
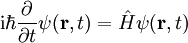
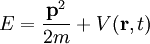
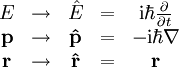
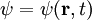 ergibt
ergibt
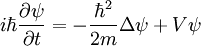 .
.
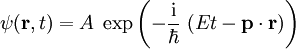 ,
,
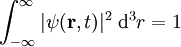
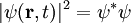 der Aufenthaltswahrscheinlichkeitsdichte des Teilchens am Ort
der Aufenthaltswahrscheinlichkeitsdichte des Teilchens am Ort 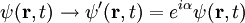 (U(1)-Symmetrie) folgt mittels des Noether-Theorems die Erhaltung der Normierung, d.h. die Wahrscheinlichkeit ist eine Erhaltungsgröße.
(U(1)-Symmetrie) folgt mittels des Noether-Theorems die Erhaltung der Normierung, d.h. die Wahrscheinlichkeit ist eine Erhaltungsgröße.
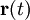 durch den mittleren Ort des Teilchens zur Zeit t, also
durch den mittleren Ort des Teilchens zur Zeit t, also
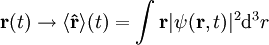
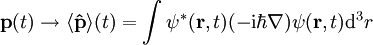 .
.
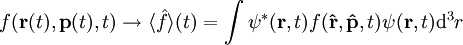 .
.
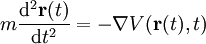
 und ist in der Physik als
und ist in der Physik als 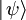 :
:
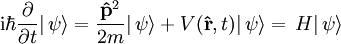 ,
,
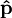 und
und 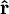 ebenfalls als basisunabhängig anzusehen sind. Diese Schreibweise erleichtert den Übergang zur mathematischen Behandlung der
ebenfalls als basisunabhängig anzusehen sind. Diese Schreibweise erleichtert den Übergang zur mathematischen Behandlung der 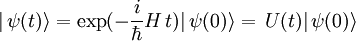
 -Potential beim Wasserstoffatom. Der nächste Abschnitt soll diesen Zusammenhang noch genauer erläutern.
-Potential beim Wasserstoffatom. Der nächste Abschnitt soll diesen Zusammenhang noch genauer erläutern.
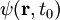 zum Zeitpunkt
zum Zeitpunkt 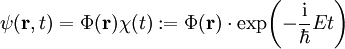
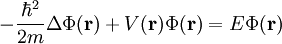 .
.
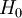 , von dem die Lösung bekannt ist, und einen kleinen Restterm
, von dem die Lösung bekannt ist, und einen kleinen Restterm 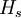 und entwickelt dann die Lösung als Störungsreihe aus der bekannten Lösung.
und entwickelt dann die Lösung als Störungsreihe aus der bekannten Lösung.
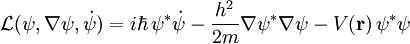
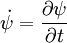 . Die Schrödingergleichung folgt dann in Analogie zum klassischen Fall aus den Lagrange´schen Bewegungsgleichungen, nur wird hier nach den Feldern und den Ableitungen der Felder differenziert statt nach Ort und Geschwindigkeit.
. Die Schrödingergleichung folgt dann in Analogie zum klassischen Fall aus den Lagrange´schen Bewegungsgleichungen, nur wird hier nach den Feldern und den Ableitungen der Felder differenziert statt nach Ort und Geschwindigkeit.
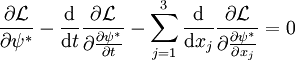
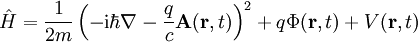 ,
,
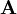 das sogenannte
das sogenannte 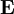 bzw. dem magnetischen Feld
bzw. dem magnetischen Feld 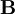 verbunden:
verbunden:
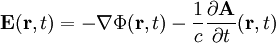
 .
.
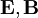 ) betrachtet. Umgekehrt beeinflusst natürlich die Wellenfunktion ψ auch das äußere elektromagnetische Feld in folgender Weise. Aus ψ und q lässt sich wieder eine elektrische Stromdichte und die Ladungsdichte des Teilchens berechnen und diese Felder erzeugen wieder ein eigenes elektromagnetisches Feld, das auf alle äußeren Ladungen und Ströme, die das äußere Feld verursachen, zurückwirkt. Würde dies in der Schrödingergleichung berücksichtigt, wäre dies ein Beispiel für eine nichtlineare Schrödingergleichung, die außer im Fall kleiner Störungen sehr viel schwieriger zu handhaben ist.
) betrachtet. Umgekehrt beeinflusst natürlich die Wellenfunktion ψ auch das äußere elektromagnetische Feld in folgender Weise. Aus ψ und q lässt sich wieder eine elektrische Stromdichte und die Ladungsdichte des Teilchens berechnen und diese Felder erzeugen wieder ein eigenes elektromagnetisches Feld, das auf alle äußeren Ladungen und Ströme, die das äußere Feld verursachen, zurückwirkt. Würde dies in der Schrödingergleichung berücksichtigt, wäre dies ein Beispiel für eine nichtlineare Schrödingergleichung, die außer im Fall kleiner Störungen sehr viel schwieriger zu handhaben ist.
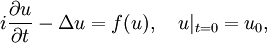 .
.
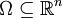
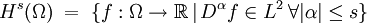 für ganzzahlige s und
für ganzzahlige s und
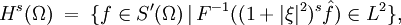 für
für 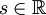 ,
,
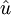 die Fouriertransformation sowie
die Fouriertransformation sowie 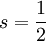 der Sprachgebrauch eine halbe Ableitung durchgesetzt. Auch kann man durchaus negative Exponenten definieren: Eine Funktion in
der Sprachgebrauch eine halbe Ableitung durchgesetzt. Auch kann man durchaus negative Exponenten definieren: Eine Funktion in 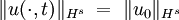
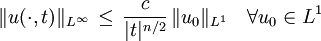 .
.


