Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Feinstruktur (Physik)Bei der genauen Betrachtung von Linienspektren von Atomen beobachtet man eine Feinstruktur. Diese zeigt sich darin, dass einzelne Linien eines Spektrums in zwei oder mehrere sehr nahe beieinanderliegende Linien aufgespalten sind. Dies bedeutet, dass es im jeweiligen Atom Energieniveaus gibt, die sehr nahe zusammen liegen, da jede Spektrallinie einem Abstand von Energieniveaus zugeordnet werden kann. Produkt-HighlightDie Größenordnung dieser feineren Aufspaltung ist jedoch im Vergleich zu den übrigen Niveaus etwa 104mal geringer. Beim Wasserstoffatom beträgt die Änderung der Wellenlängen für die Hα-, Hβ und HγLinie der Balmer-Serie 0,14 Å, 0,08 Å bzw. 0,07 Å (zum Vergleich: die Wellenlänge der Hα-Linie liegt bei 6562,8 Å). Dies erklärt auch die relativ späte Entdeckung der Feinstruktur. Diese Aufhebung der Entartung der Energieniveaus ist eine Folge der etwas anderen kinetischen Energie in der Relativitätstheorie, der Spin-Bahn-Kopplung und einem Effekt, der durch den Darwin-Term beschrieben wird. Um diese rein relativistischen Effekte in der Quantenmechanik zu berücksichtigen, addiert man zum Hamiltonoperator des Systems Korrekturterme. In erster Ordnung lautet der Hamiltonoperator dann:
wobei mec2 die Ruheenergie des Elektrons und H0 der nichtrelativistische Hamiltonoperator ist. Dabei ist WM der relativistische Korrekturterm der kinetischen Energie:
WSB ist der Korrekturterm zur Spin-Bahn-Kopplung: und WD ist der sog. Darwin-Term als Korrektur der potentiellen Energie
Die Energieverschiebung, die man als Feinstruktur bezeichnet, ist dann ΔE = EM + ESB + ED (relativistische Massenkorrektur, Spin-Bahn-Kopplung, Darwin-Term). Diese Korrekturterme treten auf, wenn man statt der nichtrelativistischen Schrödinger-Gleichung (bzw. Pauli-Gleichung) die relativistische Dirac-Gleichung für das Atom löst. Neben der Feinstruktur kann man allerdings auch noch feinere Strukturen beobachten: die Hyperfeinstruktur. GeschichtlichesFür seine Entdeckungen über die Feinstruktur des Wasserstoff-Spektrums erhielt Willis Eugene Lamb 1955 den Nobelpreis für Physik. Siehe auch: Feinstrukturkonstante |
| Dieser Artikel basiert auf dem Artikel Feinstruktur_(Physik) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





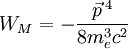 ,
,
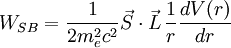
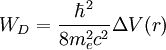 .
.


