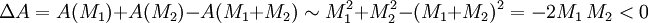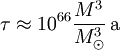Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Hawking-StrahlungDie Hawking-Strahlung ist eine vom britischen Physiker Stephen Hawking 1974 postulierte Strahlung Schwarzer Löcher. Die Herleitung des Effektes basiert sowohl auf Konzepten der Quantenmechanik als auch der Allgemeinen Relativitätstheorie. Aufgrund der semiklassischen Näherung bei der Herleitung ist dieses Phänomen jedoch noch nicht vollständig untersucht und weiterhin Gegenstand aktueller Forschung. Der Hawking-Effekt ist daher von großem Interesse, da er als potentielles Testfeld für eine quantenmechanische Theorie der Gravitation dienen könnte. Produkt-Highlight
Anschauliche Interpretation des Hawking-EffektesIm Gegensatz zur Klassischen Physik ist in der Quantenmechanik das Vakuum kein „leeres Nichts“, sondern ein kompliziertes Gebilde von Vakuumfluktuationen. Diese Vakuumfluktuationen bestehen aus virtuellen Teilchen-Antiteilchen-Paaren, die nach der quantenmechanischen Unschärferelation für kurze Zeit existieren (Siehe dazu auch: Casimir-Effekt). Die Erzeugung und Vernichtung von virtuellen Teilchen findet auch in der unmittelbaren Nähe des Ereignishorizonts Schwarzer Löcher statt. In diesem Fall kann es vorkommen, dass einer der beiden Partner den Ereignishorizont überschreitet, während der zweite Partner als reales Teilchen in den freien Raum entkommt. Das erste Teilchen kann dann nicht mehr von dem zweiten aus beobachtet (gesehen) werden, da es hinter dem Ereignishorizont verschwunden ist. Das hineinstürzende Teilchen setzt damit eine potenzielle Energie frei, die für eine Paarbildung sowie das Hinauskatapultieren des anderen Teilchens aus dem Gravitationsfeld ausreicht. Als Folge des enormen Verlusts von potenzieller Energie durch das hineinstürzende Teilchen nimmt dabei die Masse des Schwarzen Loches wider Erwarten nicht zu, sondern sogar ab. Weiterhin können die entstandenen Teilchen/Antiteilchen-Paare im Rahmen ihrer Annihilation Photonen abstrahlen, die ebenfalls in den freien Raum entkommen können, wie z. B. im Falle der Annihilation von Elektronen und Positronen, die in diesem Falle 2 um 180 Grad versetzte Gamma-Quanten mit je 511 keV abgeben, was in der Positronen-Emissions-Tomographie (PET) genutzt wird. Auf diese Weise entsteht ein Netto-Energiestrom vom Schwarzen Loch weg, sodass insgesamt Masse bzw. Energie aus dem Schwarzen Loch in den freien Raum „verdampft“. Da die Stärke der Vakuumfluktuationen durch eine starke Krümmung der Raumzeit begünstigt werden, ist dieser Effekt besonders bei Schwarzen Löchern geringer Masse bedeutsam. Schwarze Löcher geringer Masse sind von geringer Ausdehnung (Schwarzschildradius), ihr Ereignishorizont und die umgebende Raumzeit sind entsprechend stärker gekrümmt. Spektrum und GrößenabhängigkeitDiese Strahlung müsste gerade das Spektrum eines Schwarzen Körpers haben, wobei die Temperatur der Strahlung mit wachsender Masse des Schwarzen Loches sinkt. Große Schwarze Löcher, wie sie aus Supernovae entstehen, haben dadurch eine so geringe Strahlung, dass diese im Universum nicht nachweisbar ist. Kleine Schwarze Löcher hingegen haben nach dieser Theorie eine deutliche Wärmestrahlung, was dazu führt, dass ihre Masse rasch abnimmt. So hat ein Schwarzes Loch der Masse 1012 Kilogramm – der Masse eines Berges – eine Temperatur von 1012 Kelvin, so dass neben Photonen auch massebehaftete Teilchen wie Elektronen und Positronen emittiert werden. Dadurch steigt die Strahlung weiter an, sodass so ein kleines Schwarzes Loch in relativ kurzer Zeit völlig zerstrahlt. Sinkt die Masse unter 1000 Tonnen, so explodiert das Schwarze Loch mit der Energie einer Millionen-Megatonnen-Atombombe. Die Lebensdauer eines Schwarzen Loches ist proportional zur dritten Potenz seiner ursprünglichen Masse. Die Lebensdauer eines Schwarzen Loches von der Masse der Sonne beträgt 1064 Jahre, liegt also jenseits sämtlicher Beobachtungsgrenzen. Für ein kleines Schwarzes Loch liegt die Lebensdauer jedoch bei nur 1010 Jahren, was dem gegenwärtigen Alter des Universums entspricht. Demnach müsste es möglich sein, die Strahlung dieser Schwarzen Löcher aufzufangen. Die Hawking-Strahlung bedeutet eine Verletzung des zweiten Hauptsatzes der Schwarzloch-Dynamik, da die Strahlung die Masse – und damit die Horizontfläche – des Schwarzen Loches verringert. Allerdings wird gleichzeitig eine entsprechende Menge Entropie abgegeben (eben in Form thermischer Strahlung), was einen tieferen Zusammenhang zwischen beiden Größen nahe legt. Hawking-TemperaturMittels der Hawking-Entropie und der thermodynamischen Definition der Temperatur wobei h das Planck'sche Wirkungsquantum, c die Lichtgeschwindigkeit, G die Gravitationskonstante, kB die Boltzmannkonstante und M die Masse des schwarzen Loches ist. Diese Gleichung beruht auf den Näherungen des thermodynamischen Gleichgewichts. Ein Teil der erzeugten Strahlung wird durch das Gravitationfeld in das schwarze Loch zurückgestreut. Schwarze Löcher sind daher eher als „graue Strahler“ zu verstehen mit einer gegenüber dem Modell des schwarzen Körpers verminderten Strahlungs-Intensität. Die Näherungen bei der Herleitung gelten nur für Schwarze Löcher mit großer Masse. Für sehr kleine Schwarze Löcher sollte die Intensitätsverteilung deutlich von der eines Schwarzen Strahlers abweichen, weil in diesem Fall die quantenmechanischen Effekte so bestimmend werden, dass die semiklassische Näherung nicht mehr gilt. Der Hawking-Effekt stellt einen Spezialfall des Gibbons-Hawking-Effektes dar. Hawking-Entropie und verallgemeinerter zweiter HauptsatzDurch die Entropie-Gleichung von Hawking lässt sich ein Zusammenhang zwischen der Thermodynamik, der Quantenmechanik, der Relativitätstheorie und der klassischen Mechanik herstellen:
Die Herleitung dieser Gleichung benutzt das Stefan-Boltzmann-Gesetz. Dies führt zum sogenannten „verallgemeinerten zweiten Hauptsatz der Thermodynamik“. Der zweite Hauptsatz der Thermodynamik besagt, dass die Entropie eines Systems nicht mit der Zeit abnehmen kann. Die Verallgemeinerung besagt, dass die Summe aus „gewöhnlicher“ Entropie und der Gesamtfläche aller Ereignishorizonte nicht mit der Zeit abnehmen kann. Anwendung: fusionierende und zerfallende Schwarze LöcherBetrachte die Fusion zweier Schwarzer Löcher der Massen M1 und M2. Der Fusionsprozess sei isentrop, d. h. die gewöhnliche Entropie des Systems verändert sich nicht. Da die Fläche des Ereignishorizontes A proportional zum Quadrat der Masse ist, ergibt sich für die Änderung ΔA = Anachher − Avorher: Die Gesamtfläche nimmt also zu und die Fusion zweier Schwarzer Löcher steht somit nicht im Widerspruch zum verallgemeinerten zweiten Hauptsatz. Betrachte nun den Zerfall eines Schwarzen Loches der Masse M1+M2 in zwei kleinere Schwarze Löcher der Massen M1 und M2. Der Zerfallssprozess sei wieder isentrop. Für die Änderung der Gesamtfläche der Ereignishorizonte gilt dann: Die Gesamtfläche würde also bei dem Zerfall eines Schwarzen Loches in zwei kleinere abnehmen. Der verallgemeinerte zweite Hauptsatz der Thermodynamik verbietet also den Zerfall eines Schwarzen Loches in zwei kleinere. Schlussfolgerungen und AusblickDie Vorhersage der Hawking-Strahlung beruht auf der Kombination von Effekten der Quantenmechanik und der allgemeinen Relativitätstheorie sowie der Thermodynamik. Da eine Vereinheitlichung dieser Theorien bisher nicht gelungen ist (Quantentheorie der Gravitation), sind solche Vorhersagen immer mit einer gewissen Unsicherheit behaftet. Mit der thermischen Strahlung verliert das Schwarze Loch Energie, bzw. Masse, dadurch „schrumpft“ es mit der Zeit. Nimmt man ein Schwarzkörperspektrum, sowie ein Boltzmann-Gesetz für die Intensität an, so lässt sich eine Strahlungsleistung und daraus eine Lebensdauer τ für ein Schwarzes Loch herleiten, die proportional zur dritten Potenz der Masse ist: Schwarze Löcher stellaren Ursprungs haben jedoch aufgrund ihrer großen Masse eine geringere Temperatur als die kosmische Hintergrundstrahlung, weshalb diese Schwarzen Löcher thermische Energie aus ihrer Umgebung aufnehmen. In diesem Fall ist kein Schrumpfen des Schwarzen Loches möglich; im Gegenteil, durch die Aufnahme der Strahlungsenergie nimmt die Masse gemäß der Einsteinschen Masse-Energie-Äquivalenzformel zu. Erst wenn die Umgebungstemperatur unter die Temperatur des Schwarzen Loches gefallen ist, verliert das Loch durch die Strahlungsemission an Masse. Experimentell nachgewiesen wurde die Hawking-Strahlung bisher nicht. Für Schwarze Löcher lassen sich Gesetze herleiten, die weitgehend analog zu den drei Hauptsätzen der klassischen Thermodynamik sind. Heuristische Überlegungen führten J. D. Bekenstein bereits 1973 zu der Hypothese, dass die Oberfläche des Ereignishorizonts ein Maß für die Entropie eines Schwarzen Loches sei. Mit der Entropiefunktion und der Temperaturdefinition kann ein (verallgemeinerter) 2. Hauptsatz der Thermodynamik für Schwarze Löcher aufgestellt werden. Was am „Ende seiner Lebenszeit“ mit einem Schwarzen Loch geschieht, ist noch unklar. Insbesondere tritt dabei das so genannte Informationsparadoxon auf. Es besteht in der Frage, was beim „Verdampfen“ mit den Informationen geschieht, die vorher in das Schwarze Loch hineingestürzt sind und die nach konventioneller Auffassung nicht verloren sein können. Siehe auch
|
|
| Dieser Artikel basiert auf dem Artikel Hawking-Strahlung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





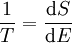 lässt sich einem Schwarzen Loch auch eine Temperatur zuordnen. Diese Temperatur
lässt sich einem Schwarzen Loch auch eine Temperatur zuordnen. Diese Temperatur 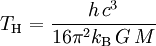
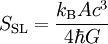
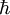 -
-