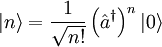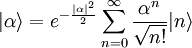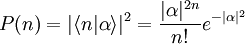Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Harmonischer Oszillator (Quantenmechanik)Der harmonische Oszillator in der Quantenmechanik, auch quantenharmonischer Oszillator, beschreibt – analog zum harmonischen Oszillator in der klassischen Physik – das Verhalten eines Teilchens (hier beschrieben durch eine Wellenfunktion) in einem harmonischen Potential. Ein Beispiel der klassischen Physik ist ein Massenpunkt an einer Feder. Dieser Massenpunkt, welcher sich in einem harmonischen Potential Der quantenharmonische Oszillator ist ein wichtiges Modellsystem der Physik, da es eines der wenigen geschlossen (also ohne Näherungen und numerische Methoden) lösbaren Systeme der Quantenmechanik ist. Mit ihm können einen Reihe physikalischer Sachverhalte näherungsweise beschrieben werden:
Produkt-Highlight
GeschichteIm Jahr 1900 entwickelte Max Planck eine Formel zur Beschreibung der gemessenen Frequenzverteilung der von einem Schwarzkörper emittierten Strahlung, wobei er von der Annahme ausging, dass der schwarze Körper aus Oszillatoren mit diskreten Energieniveaus besteht[1]. Über die geschichtliche Entwicklung der Quantenmechanik, siehe Hauptartikel Quantenmechanik - Geschichte EinführungDie klassische Hamilton-Funktion für ein Teilchen mit der Masse m in einem harmonischen Potential Die Hamilton-Funktion beschreibt hier die Gesamtenergie des Systems, also die Summe aus kinetischer Energie (erster Term) und potentieller Energie (zweiter Term). Nun werden der Ort
Im eindimensionalen Fall reduziert sich der Nabla-Operators Die Schrödinger-Gleichung des SystemsMit dem oben beschriebenen Hamilton-Operator erhält man die Eigenwertgleichung – (stationäre) Schrödinger-Gleichung – des harmonischen Oszillators.
in der Ortsdarstellung Eigenschaften der Lösungen der Schrödinger-GleichungEigenfunktionen
Die Eigenfunktionen
Dabei sind Hn(x) die hermiteschen Polynome. Der Term Der Grundzustand n = 0 hat die Form einer Gauß-Kurve
Die nebenstehende Grafik zeigt die ersten acht Lösungen
Erlaubte EnergieniveausDie Quantentheorie fordert, dass die physikalisch möglichen Zustände normierbare Lösungen der Schrödinger-Gleichung sind, d. h. im Hilbertraum liegen. Während die Differentialgleichung Lösungen für beliebige Energien hat, ergibt sich aus der Forderung nach Normierbarkeit
dass nur diskrete Energien möglich sind, wobei n eine natürliche Zahl oder Null ist. Nullpunktsenergie
Das obige Ergebnis hat fundamentale Folgen: Der harmonische Oszillator kann nicht mehr beliebige Energiemengen aufnehmen, sondern nur ganzzahlige Vielfache von Daraus folgt, dass ein quantenmechanischer harmonischer Oszillator selbst am absoluten Temperaturnullpunkt Man kann diesen Sachverhalt auch mit der Heisenbergsche Unschärferelation beschreiben. Im klassischen Fall hat das oszillierende Teilchen die exakte Position x = 0 und den exakten Impuls p = 0. In der Quantenmechanik besitzt ein Teilchen keinen exakten Ort und keinen exakten Impuls. Die Standardabweichung beider Observablen ist über die Unschärferelation verknüpft. Daher kann der Ort und der Impuls des Teilchens nur bis zu einer gewissen Grenze gleichzeitig angegeben werden. Dies lässt sich als Art räumliche „Verschmierung“ beschreiben, welche eine kinetische Mindestenergie des Teilchens zur Folge hat. Dass in der quantenmechanischen Beschreibung auch außerhalb des harmonischen Potentials eine Aufenthaltswahrscheinlichkeit für das Teilchen existiert, liegt daran, dass das Teilchen durch die endlich hohe Potentialwand getunnelt werden kann (siehe Tunneleffekt). Alternativer Lösungsweg: OperatormethodeDas Problem des harmonischen Oszillators in der Quantenmechanik lässt sich mithilfe der Methode der Erzeugungs- und Vernichtungsoperatoren behandeln. Sie wurde von Paul Dirac, basierend auf Arbeiten von Niels Bohr und Otto Wiener, entwickelt. Dieser Lösungsweg wird auch algebraische Methode genannt. Für diesen Lösungsweg definiert man zwei Operatoren
Diese Formel macht die Namensgebung sofort plausibel, weil die Anwendung von Nun lässt sich der Hamilton-Operator mit diesen neuen Operatoren umschreiben, zu: Die Operatoren
Zur Bestimmung der Eigenfunktionen kann man nun die Schrödingergleichung für den niedrigsten Zustand Diese Methode ist ein sehr eleganter Weg den harmonischen Oszillator zu behandeln. Sie hat aber noch wesentlich weitreichendere Anwendungen. Stellt man sich etwa elektromagnetische Strahlung, aus Photonen zusammengesetzt vor, so kommt man leicht dazu für Photonen ebenfalls Erzeugungs- und Vernichtungsoperatoren aufzustellen. Tatsächlich lässt sich sogar zeigen, dass man das elektromagnetische Feld als Ansammlung von harmonischen Oszillatoren beschreiben kann. Dabei steht jeder Oszillator für eine Lichtwelle bestimmter Frequenz ω. Dabei gibt dann n die Anzahl der Photonen in dieser „Mode“ des Lichtfeldes an. Allgemein nennt man ein solches Vorgehen zweite Quantisierung. klassischer GrenzfallIm Grenzfall großer Quantenzahlen n geht die Aufenthaltswahrscheinlichkeit in die klassische Aufenthaltswahrscheinlichkeit über. Diese klassische Wahrscheinlichkeitsdichte ist proportional zur inversen Geschwindigkeit 1/v. Je kleiner diese Geschwindigkeit v des klassischen Teilchens im Potential ist, desto länger verweilt es an einem entsprechenden Ort. Die Geschwindigkeit kann man direkt aus dem Energiesatz ableiten. Die folgende Abbildung zeigt die klassische und die quantenmechanische Aufenthaltswahrscheinlichkeitsdichte. Je größer n wird, desto ähnlicher werden sich die Kurven: Quasiklassische ZuständeBringt man ein lokalisiertes Wellenpaket in ein harmonisches Potential (siehe Abbildung rechts), so verhält es sich, wie ein klassisches Teilchen in diesem Potential (daher quasiklassischer Zustand). Trifft es auf die Potentialränder, so wird es umdrehen und zurücklaufen. Effektiv führt es dann eine Schwingung im Potential aus. Mathematisch entsprechen diese Zustände den sog.kohärenten Zuständen. Sie werden durch eine komplexe Zahl α charakterisiert und lassen sich als Linearkombination der Zustände Wichtig sind solche Zustände bei der Beschreibung von kohärenter Strahlung, da man zeigen kann, dass sich das Lichtfeld in der Quantenfeldtheorie auf harmonische Oszillatoren (einer für jede Mode des Feldes) zurückführen lässt (siehe auch kohärente Strahlung). Die Wahrscheinlichkeitsverteilung der Besetzungszahlen kohärenter Zustände folgt (wie die Photonenstatistik von kohärentem Licht) der Poisson-Verteilung:
Zunächst wird mit einem Laserpuls eine tiefliegende, schmale Wellenfunktion in einen höheren Energiezustand angehoben. Dort bleibt sie weiter lokalisiert und beginnt sich als „quasiklassischer Zustand“ im Potential zu bewegen. Zur Messung wird dann ein zweiter Puls eingestrahlt, der das Molekül ionisiert. Die Position der Wellenfunktion gibt den Abstand der Atome im Molekül an. Aus der kinetischen Energie der Bruchstücke kann auf diesen Abstand und die Form des Wellenpakets geschlossen werden. Quellen
Links
Einzelquellen
|
|
| Dieser Artikel basiert auf dem Artikel Harmonischer_Oszillator_(Quantenmechanik) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


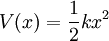 befindet, erfährt eine, der Auslenkung aus der Ruhelage proportionale, Rückstellkraft:
befindet, erfährt eine, der Auslenkung aus der Ruhelage proportionale, Rückstellkraft: 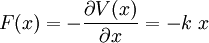 , wobei
, wobei 


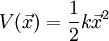 mit
mit 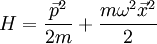
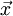 und der Impuls
und der Impuls 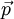 durch die entsprechenden quantenmechanischen Operatoren ersetzt (Korrespondenzprinzip):
durch die entsprechenden quantenmechanischen Operatoren ersetzt (Korrespondenzprinzip):
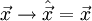 und
und
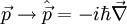
 bezeichnet den Nabla-Operator. Der letzte Teil der Ausdrücke ist jeweils die Ortsdarstellung der Operatoren. Damit geht die klassische Hamilton-Funktion in den
bezeichnet den Nabla-Operator. Der letzte Teil der Ausdrücke ist jeweils die Ortsdarstellung der Operatoren. Damit geht die klassische Hamilton-Funktion in den 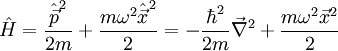
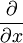 . Im Folgenden wird zunächst nur der eindimensionale Fall betrachtet.
. Im Folgenden wird zunächst nur der eindimensionale Fall betrachtet.
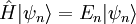 ,
,
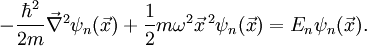
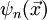 des harmonischen Oszillators ergeben sich durch Lösen der obigen Differentialgleichung. Es sind die hermiteschen Funktionen
des harmonischen Oszillators ergeben sich durch Lösen der obigen Differentialgleichung. Es sind die hermiteschen Funktionen
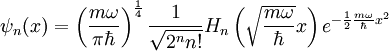 .
.
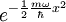 beschreibt den exponentiellen Abfall außerhalb des Oszillatorpotentials.
beschreibt den exponentiellen Abfall außerhalb des Oszillatorpotentials.
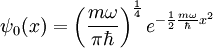 .
.
 ,
,
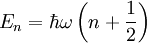
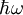 . Der Zustand mit der niedrigsten Energie ist
. Der Zustand mit der niedrigsten Energie ist 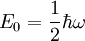 .
.
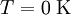 noch die Energie
noch die Energie 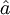 und
und 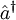 , die einem Oszillator jeweils ein Energiequant
, die einem Oszillator jeweils ein Energiequant 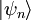 (siehe auch
(siehe auch 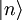 überführt. Ein solcher Zustand heißt Fock-Zustand oder Besetzungszahlzustand, weil er die Anzahl n der Energiequanten im Oszillator angibt. Man definiert diese Operatoren so, dass sie folgende Beziehungen erfüllen:
überführt. Ein solcher Zustand heißt Fock-Zustand oder Besetzungszahlzustand, weil er die Anzahl n der Energiequanten im Oszillator angibt. Man definiert diese Operatoren so, dass sie folgende Beziehungen erfüllen:
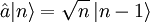 und
und 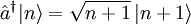
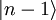 führt und für
führt und für 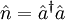 zusammensetzen, der die Anzahl der Energiequanten in einem Zustand (also die Zahl n) liefert:
zusammensetzen, der die Anzahl der Energiequanten in einem Zustand (also die Zahl n) liefert:
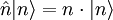
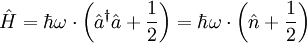
 und
und  darstellen::
darstellen::
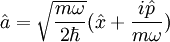
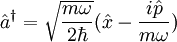
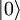 explizit lösen (dies ist eine sehr einfache Differentialgleichung) und erhält so dessen Ortsdarstellung. Alle weiteren Zustände erhält man dann über rekursive die Anwendung des Erzeugungsoperators auf diesen Grundzustand:
explizit lösen (dies ist eine sehr einfache Differentialgleichung) und erhält so dessen Ortsdarstellung. Alle weiteren Zustände erhält man dann über rekursive die Anwendung des Erzeugungsoperators auf diesen Grundzustand: