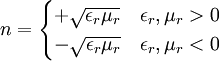Metamaterial

Ein Metamaterial ist eine künstlich hergestellte Struktur, deren elektromagnetischen Eigenschaften wie bei einem üblichen Material durch Permittivität ε_r und Permeabilität μ_r beschrieben werden können, wobei diese beiden Parameter jedoch in der Natur nicht vorkommende Werte aufweisen.

Reelle, negative Brechzahlen

sind von besonderem Interesse, zunehmend jedoch auch positiv reelle Werte kleiner 1. Negative Brechzahlen bedingen antiparallele Phasen- und Gruppengeschwindigkeit. Wellen mit dieser Eigenschaft sind als Backward Waves seit 1905 (Pocklington) bekannt und wurden in Oszillatoren und Verstärkern lange benutzt. 1960 wurde durch Veselago theoretisch vorhergesagt, dass ein hypothetisches Material mit negativer Brechzahl Backward-Waves bedingt und welche Auswirkungen dies hat ^[1].

Da keine natürlichen Materialien mit diesen Eigenschaften existieren bzw. bisher gefunden wurden, werden sie synthetisiert, meist durch periodische Anordnung von Zellen.

Die Definition von Metamaterialien ist noch im Fluss, die geläufigere beschränkt die Zellgröße auf (deutlich) kleiner als eine viertel Freiraumwellenlänge. Manche Autoren beziehen photonische Kristalle, bei denen die Zellgröße in der Größenordnung einer halben Wellenlänge liegt, mit ein. Erstere, geläufigere Definition bedeutet, dass sich die Anordnung wie ein effektives Medium verhält, d. h. nicht in erster Linie die Zellgröße (wie bei photonischen Kristallen und Frequency Selective Surfaces), sondern der Zellinhalt die Funktion bestimmt.

Weiteres empfehlenswertes Fachwissen

Lassen Sie sich von statischen Aufladungen nicht die Wägegenauigkeit stören.

Was ist die Empfindlichkeit meiner Waage?

Leitfaden für die Waagenreinigung: 8 einfache Schritte

Elektromagnetische Eigenschaften von Materialien mit negativer Brechzahl

Der sowjetischen Physiker Victor Veselago untersuchte 1968 theoretisch die Ausbreitung elektromagnetischer Wellen in Materialien mit negativer Brechzahl und deren Rändern. Phasengeschwindigkeit und Energieflussrichtung (Pointingvektor) im Material mit negativer Brechzahl sind antiparallel, wie bei den schon länger bekannten Backward Waves. In diesem Fall formen der Wellenvektor, die elektrische Feldstärke und die magnetische Feldstärke ein linkshändiges Dreibein – daher die Bezeichnung „linkshändiges Material“.

Er zeigte, dass dies zu inverser Tscherenkow-Strahlung, inversem Doppler-Effekt und inversem Snell'schen Brechungsgesetz führt. Letzteres beschreibt, dass beim Übergang vom optisch dünneren zum optisch dichteren Medium die Welle zum Lot hingebrochen wird. Die Brechzahl, eine normalerweise positive Zahl, beschreibt, wie Licht oder andere elektromagnetische Strahlung beim Übergang in das jeweilige Material abgelenkt wird. Bei Stoffen mit negativer Brechzahl wird ein auftreffender Lichtstrahl nicht, wie bei herkömmlichen Stoffen zum Lot hin gebrochen, sondern über das Lot hinaus in die negative Richtung. Der Lichtstrahl befindet sich also sowohl innerhalb als auch außerhalb des Materials auf derselben Seite des Einfallslots. Das inverse Snell'sche Gesetz führt bei gekrümmten Flächen zu einer Vertauschung von konvergenter und divergenter Strahlführung, d. h., konkave Linsen bündeln, konvexe Linsen streuen.

Zusätzlich wurde von Scharidow gezeigt, dass die Strahlverschiebung beim Goos-Hänchen-Effekt ebenfalls das Vorzeichen wechselt.

Herstellung

In der Natur kommen Materialien mit negativer Permittivität und gleichzeitig negativer Permeabilität nicht vor, d. h. solche Materialien müssen synthetisiert werden. Die Synthetisierung muss nicht zwingend periodisch erfolgen, die erleichtert jedoch die Berechnung und wird daher von allen Gruppen angewandt. Es gibt resonante und nichtresonante Ansätze:

Zur ersten Gruppe gehören der Split-Ring/Wire-Grid-Ansatz und der Ansatz über dielektrische Kugeln unterschiedlichen Durchmessers in einem NaCl-Gitter.

Beim Split-Ring/Wire-Grid-Ansatz führt das Drahtgitter zu negativer Permittivität, da sich in Metallen unterhalb der Plasmonresonanz Elektronen wie ein Plasma verhalten (Drude-Modell). Ein Resonator, der meistens als (Doppel-)Ring mit Spalt ausgeführt ist, führt zu einem magnetischen Dipolmoment und in einem engen Frequenzbereich zu einer negativen effektiven Permeabilität. Das Resonatordesign ist so zu wählen, dass sich im gewünschten Frequenzbereich eine negative Brechzahl ergibt.

Diese Anordnung zeigt das Problem, dass geringe Verluste mit (sehr) geringer Bandbreite einhergehen, andererseits auf hohe Verluste hin entworfene Strukturen zwar erträgliche Bandbreiten ermöglichen, dann aber der Transmissionskoeffizient sinkt. Da metallische Verluste mit der Frequenz steigen, sind derartige Metamaterialstrukturen im optischen Frequenzbereich schwerlich noch von Absorbern zu unterscheiden.

Der Ansatz über dielektrische Kugeln hat den Vorteil, dass als nicht-metallische Struktur auch der optische Frequenzbereich erschlossen werden könnte. Die theoretische Arbeit zu diesem Ansatz zeigt jedoch, dass nur sehr geringe Bandbreiten zu erwarten sind und entsprechend extreme Anforderungen an die Toleranzen der Fertigungstechnologie gestellt würden.

Möglicher Ausweg aus der Bandbreiten-/Dämpfungsproblematik, zumindest im Mikrowellenbereich, sind nichtresonante Konzepte, die auf inversen Leitungsstrukturen basieren. Diese bandpassartigen Strukturen bieten gleichzeitig hohe Bandbreite und geringe Verluste – solange Strukturen entworfen werden können, die sich wie diskrete Serien- und Parallelresonatoren verhalten. Aufgrund der Ableitung aus der Leitungstheorie waren erste derartige Metamaterialien eindimensional und erreg(t)en die Kontroverse, ob es sinnvoll ist, von Metamaterialien oder von angewandter Filtertheorie zu sprechen. Verallgemeinerungen auf (isotrope) 2D/3D-Anordnungen wurden theoretisch vorgestellt, einige auch experimentell nachgewiesen.

2007 ist der Split-Ring-Ansatz überwiegend bei Mitgliedern der Physik-Community zu finden. Der nichtresonante, leitungsbasierte Ansatz ist eher in der Elektrotechnik anzutreffen, beginnt jedoch auch in der Physik Fuß zu fassen.

Mögliche Anwendungen

Die von Veselago analysierten planaren Linsen sind aufgrund der fehlenden optischen Achse potenziell vorteilhaft, die von Pendry vorgeführte Auflösungsverbesserung führte zu besonders großer Aufmerksamkeit in Physik und Elektrotechnik ^[2]. Sie ist dadurch gekennzeichnet, dass eine punktförmige Lichtquelle ein punktförmiges Abbild hat, d. h. im Gegensatz zur üblichen Linse wird das evaneszente Wellenvektorspektrum der Quelle durch die planare Metamateriallinse resonant verstärkt und dann im Bild 'rekonstruiert'. Dies ist nicht mit endlicher Auflösung bei üblichen Linsen aufgrund endlicher Eingangspupille zu verwechseln, Beugungsbegrenzung ist als Vergleichskriterium nicht heranziehbar, denn Pendrys Linse ist unendlich groß.

2006 wurde des weiteren in ^{[3] [4]} theoretisch und experimentell ein Konzept vorgestellt, wie mit Hilfe einer Metamaterialumhüllung eine Tarnkappenwirkung erzielt werden kann. Dieses Konzept basiert nicht auf negativen Brechzahlen, sondern einer kontinuierlichen, anisotropen Variation der Brechzahl zwischen 0 und 1. Dieses Konzept ist Luneberg-Linsen nicht gänzlich unähnlich.

Als potenzielle Anwendung könnte man jedes bisher bestehende Abbildungssystem nennen, und auch Pendrys Tarnkappe ließe sich als spezielles metamaterialbasiertes Abbildungssystem klassifizieren. Bei allen Szenarien ist jedoch zu beachten, dass endliche Zellgröße, Verluste, endliche Abmessungen der Linse und Dispersion die Auflösung begrenzen und zu Aberrationen führen.

Im Optischen arbeitende Systeme sind in weiter Ferne, hierfür sind 3D-Metamaterialien nötig, und es sind noch nicht einmal eindimensionale, nicht übermäßig dämpfende Metamaterialien im Optischen publiziert. Deshalb ist noch der Mikrowellenbereich von besonderem Interesse, womöglich wird sich der Fokus später zu höheren Frequenzen verschieben, ähnlich der Entwicklung vom MASER zum LASER.

Publizierte Mikrowellen-Anwendungen sind z. B. (steuerbare) Richtantennen, Koppler, Radome, Reflektoren, Phasenschieber/-kompensatoren, Abbildungssysteme und (bei Einsatz von aktiven Komponenten) auch Solitonkonzepte.

Einige metamaterialbasierten Anwendungs-Konzepte sind mit Vorsicht zu genießen: Es ist eben nicht möglich, ein hypothetisches Material mit negativer Brechzahl anzunehmen und dann wild zu spekulieren, was damit alles möglich wäre. Die oben erwähnten Parameter wie endliche Größe einer Metamaterialzelle, Verluste, Dispersion etc. sind nicht vernachlässigbare Sekundäreffekte, sondern entscheidend. Als Beispiel sei ein Vorschlag genannt, den Strahlungswiderstand Hertz'scher Dipole durch Metamaterialummantelung zu erhöhen und dadurch kleine Antennen zu ermöglichen. Der amüsant zu lesende Verriss dieses Konzepts ist in ^[5] zu finden.

Quellen

1. ↑ V.G. Veselago, The electrodynamics of substances with simultaneously negative values of ε and µ, Sov. Phys. Usp. 10, 509 (1968)
2. ↑ JB Pendry, Negative Refraction Makes a Perfect Lens, Phys. Rev. Lett. 85, 3966 (2000)
3. ↑ J.B. Pendry and D. Schurig and D.R. Smith, 'Controlling Electromagnetic Fields, Science 312, 1780 (2006)
4. ↑ D. Schurig and J.J. Mock and B.J. Justice and S.A. Cummer and J.B. Pendry and A.F. Starr and D.R. Smith, 'Metamaterial Electromagnetic Cloak at Microwave Frequencies, Science 314, 977 (2006)
5. ↑ R.C. Hansen, Electrically Small, Superdirective and Superconducting Antennas, Wiley, 2006

Literatur

• V.G. Veselago, Sov. Phys. Usp. 10, 509 (1968)
• J. B. Pendry, Nature 423, 22 (2003)
• Sergei Tretyakov, "Analytical Modeling in Applied Electrodynamics", Artech House, 2003
• C. Caloz and T. Itoh, "Electromagnetic Metamaterials", Wiley, 2005
• G.V. Eleftheriades and K.G. Balmain, "Negative-Refraction Metamaterials", Wiley, 2005
• N. Engheta and R.W. Ziolkowski, "Electromagnetic Metamaterials", Wiley, 2006