Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Symmetrieadaptierte LinearkombinationSymmetrieadaptierte Linearkombination (SALK) aus Atomorbitalen (AO´s) dient zur Konstruktion von Molekülorbitalen (MO´s) nach der LCAO-Näherung (linear combination of atomic orbitals). Produkt-HighlightUm aus zwei AO´s ein MO zu konstruieren sind folgende Sätze nützlich:
Die MO´s eines Moleküls tauchen als irreduzible Darstellungen in der Charaktertafel des Moleküls auf. BeispielKombination zweier 1s-Orbitale Es gibt hier zwei Kombinationsmöglichkeiten: + - (ungerade) und + + (gerade) Ein solches Molekül gehört zur Punktgruppe
Die reduziblen Darstellungen sind hier 2,2,2,0,0,0. Durch Ausreduzieren erhält man die irreduziblen Darstellungen:
In der ersten Spalte der Charaktertafel stehen immer nur einsen. Um durch Addition auf die reduziblen Darstellungen oben zu kommen, 1+1=2 und 1+(-1)=0, müssen die irreduziblen Darstellungen Γ + und Γ − folgendermaßen aussehen:
Die irreduziblen Darstellungen kann man auch so erklären:
im Beispiel:
--> Als Basis für eine LCAO-Näherung mit 1s-Orbitalen sollte man Γ + und Γ − verwenden. |
|||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Symmetrieadaptierte_Linearkombination aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





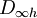 , dessen Charaktertafel so aussieht:
, dessen Charaktertafel so aussieht:
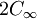
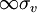
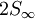
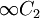
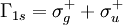 . Die Bezeichnungen kommen daher, dass es sich hier um
. Die Bezeichnungen kommen daher, dass es sich hier um 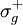 ändert keine der Operationen etwas (+ + --> + +)
ändert keine der Operationen etwas (+ + --> + +)
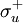 ändern Identität, Drehung um unendlichzählige Achse oder Spiegelung um eine der unendlich vielen Spiegelebenen nichts. Inversion, Drehspiegelung oder Drehung um eine der zweizähligen Achsen invertieren die Funktion (+ - --> - +)
ändern Identität, Drehung um unendlichzählige Achse oder Spiegelung um eine der unendlich vielen Spiegelebenen nichts. Inversion, Drehspiegelung oder Drehung um eine der zweizähligen Achsen invertieren die Funktion (+ - --> - +)


