Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Symmetriegruppe
In der mathematischen Gruppentheorie ist die Symmetriegruppe eines geometrischen Objektes die Gruppe, die aus der Menge aller Kongruenzabbildungen besteht, die das Objekt auf sich selbst abbilden, zusammen mit der Verkettung von Abbildungen als Gruppenoperation. Produkt-Highlight
BegriffsklärungDiese Begriffe beschreiben mögliche Eigenschaften eines Objektes. Um zu erkennen, welcher Symmetriegruppe das Objekt angehört, muss festgestellt werden, welche dieser Eigenschaften zutreffen. DiskretheitEine Symmetriegruppe weist intuitiv gesehen dann eine diskrete Topologie auf, wenn es so etwas wie „kleinste Schritte“ gibt. Beispielsweise ist eine Gruppe von Drehungen um einen Punkt genau dann diskret, wenn alle möglichen Drehwinkel Vielfache eines kleinsten Winkels sind. Sind hingegen auch beliebig kleine Drehwinkel in der Gruppe enthalten, so ist diese Gruppe nicht diskret. Allgemein hat jede Gruppe mit endlich vielen Elementen eine diskrete Topologie. Eine diskrete Gruppe lässt sich aus endlich vielen Symmetrieoperationen durch Komposition erzeugen. Der Umkehrschluss gilt jeweils nicht. Praktisch gesehen ist eine Symmetriegruppe genau dann diskret, wenn es eine untere Schranke gibt sowohl für die Längen aller (von Null verschiedenen) Verschiebungen als auch für die Drehwinkel aller Drehsymmetrien. PeriodizitätMan betrachtet die Menge aller in der Gruppe enthaltenen (von Null verschiedenen) Verschiebungen (Translationen) und bestimmt, wie viele dieser Vektoren linear unabhängig voneinander sind. Formal gesprochen bestimmt man die Dimension des Spanns dieser Verschiebungsvektoren. Enthält die Gruppe überhaupt keine Verschiebungen, so gibt es mindestens einen Punkt, der Fixpunkt aller Abbildungen ist. Man spricht in diesem Fall von einer Punktgruppe. Punktgruppen sind genau dann endlich, wenn sie diskret sind. Sobald die Gruppe mindestens eine Verschiebung enthält, enthält sie zumindest in euklidischer Geometrie automatisch unendlich viele Elemente. Entspricht die Zahl der linear unabhängigen Verschiebungsvektoren der Dimension des Raumes, in den das Objekt eingebettet ist, so gibt es einen beschränkten Teil des Objekts (eine Zelle), deren Bilder den gesamten Raum ausfüllen. Ist die Gruppe zusätzlich auch noch diskret, so spricht man von einer Raumgruppe und nennt das Muster periodisch. In diesem Fall gibt es einen beschränkten Fundamentalbereich von gleicher Dimension wie der Raum, also beispielsweise in der Ebene mit einer von Null verschiedenen Fläche. Zweidimensionale euklidische GeometrieDie Symmetriegruppen in der euklidischen Ebene lassen sich wie folgt klassifizieren:
Andere Dimensionen
Siehe auch
|
|
| Dieser Artikel basiert auf dem Artikel Symmetriegruppe aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





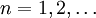 ), das sind alle Drehungen um einen Punkt um Vielfache von
), das sind alle Drehungen um einen Punkt um Vielfache von