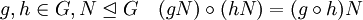Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Gruppentheorie
Die Gruppentheorie, als mathematische Disziplin im 19. Jahrhundert entstanden, ist ein Wegbereiter der modernen Mathematik. Beispielsweise folgt die Gruppe, die aus den Drehungen eines regulären n-Ecks in der Ebene um Vielfache des Winkels 360°/n besteht, denselben Gesetzen wie die Addition der ganzen Zahlen modulo n. Neutrales Element – entsprechend der Null bei der Addition – wäre hier die Nicht-Drehung oder äquivalent die Drehung um einen Winkel von 0°. Große Beiträge zur Gruppentheorie stammen unter anderem von Evariste Galois, Niels Henrik Abel und Sophus Lie. Knappe Begriffsdefinitionen finden sich im Gruppentheorie-Glossar. Produkt-Highlight
Erklärung für Nicht-MathematikerGruppen werden in der Mathematik verwendet, um vom Rechnen mit konkreten Zahlen zu abstrahieren (sprich: um mit Symbolen anstelle von Zahlen zu rechnen). Entsprechend besteht eine Gruppe aus einer Menge von abstrakten Dingen oder Symbolen und einer „Rechenvorschrift“ (Verknüpfung), die angibt, wie mit diesen Dingen umzugehen ist. Genauer gesagt: Von einer Gruppe spricht man, falls für eine Menge zusammen mit einer Verknüpfung je zweier Elemente dieser Menge, zum Beispiel „a × b“, die folgenden weiteren Anforderungen erfüllt sind:
Spezialfall: Wenn man zudem noch die Operanden vertauschen darf, also a × b = b × a gilt (Kommutativität), dann liegt eine abelsche Gruppe vor. Beispiele für abelsche Gruppen sind
Die sehr allgemeine Definition von Gruppen ermöglicht es, nicht nur Mengen von Zahlen mit entsprechenden Operationen als Gruppen aufzufassen, sondern auch andere abstrakte Dinge und Symbole, die die geforderten Eigenschaften erfüllen wie zum Beispiel N-Ecke mit ihren Drehungen und Spiegelungen. siehe auch: Diedergruppe Mathematische Definition des GruppenbegriffsDefinitionEin Paar
Eine Gruppe
Bei dieser Definition darf nicht übersehen werden, dass die Verknüpfung Bemerkungen zur NotationHäufig wird für die Verknüpfung Die Gruppeneigenschaften lassen sich auch additiv notieren, indem für die Verknüpfung Ist die Verknüpfung klar, so schreibt man für die Gruppe häufig nur G. Abschwächung der DefinitionDie Gruppenaxiome können formal abgeschwächt werden, indem man die Axiome für das neutrale und das inverse Element folgendermaßen ersetzt:
Diese formal schwächere Definition ist äquivalent zu der ursprünglichen Definition, denn es gilt:
Grundlegende Eigenschaften einer Gruppe
Grundkonzepte der GruppentheorieOrdnung einer GruppeDie Mächtigkeit (Kardinalität) | G | der Trägermenge der Gruppe nennt man Ordnung der Gruppe oder kurz Gruppenordnung. Für endliche Mengen ist dies einfach die Anzahl der Elemente. Ordnung von ElementenHauptartikel: Ordnung eines Gruppenelementes Ergibt ein Element a der Gruppe endlich viele Male mit sich selbst verknüpft das neutrale Element 1, d. h. es gilt: an = 1, so nennt man das kleinste derartige n die Ordnung des Elements a. Falls kein solches n existiert, sagt man, dass a unendliche Ordnung hat. In beiden Fällen entspricht die Ordnung des Elements der Ordnung der von ihm erzeugten Untergruppe. Davon ausgehend kann man zeigen, dass die Ordnung jedes Elements einer endlichen Gruppe endlich ist und die Gruppenordnung teilt. UntergruppenIst H eine Teilmenge der Trägermenge G einer Gruppe Hierzu ein wichtiger Satz: (Satz von Lagrange) Die Ordnung (Anzahl der Elemente) jeder Untergruppe H einer endlichen Gruppe G ist ein Teiler der Ordnung der Gruppe G. Ist speziell | G | eine Primzahl, dann hat G nur die (trivialen) Untergruppen {e} (bestehend aus dem neutralen Element) und G selbst. Die Anzahl der Elemente einer Gruppe heißt auch ihre Ordnung. NebenklassenDefiniert man auf der Menge G die Relation ˜ durch:
erhält man eine Äquivalenzrelation
auf G. Die sog. Äquivalenzklasse zu einem Element
und bezeichnet sie durch Die Menge aller Linksnebenklassen von H bezeichnet man mit G / H. Definiert man eine andere Relation a˜b durch
so ergibt sich die Menge der zu a äquivalenten Elemente in G als
Diese Menge entsteht also durch Rechtsverknüpfung der Elemente aus H mit dem Element a; sie wird entsprechend mit Beispiel: Man nehme die ganzen Zahlen mit der Addition als G. Dann ist die Menge H aller ganzzahligen Vielfachen von 3 eine Untergruppe. Bildet man die rechten Nebenklassen, so erhält man folgende Tabelle: H H+1 H+2 H+3=H H+4=H+1 ... ... ... ... -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 ... ... ... Man sieht, dass diese Tabelle wieder genau alle ganzen Zahlen enthält, wobei keine Zahl zweimal vorkommt. Für endliche Gruppen besagt der Satz von Lagrange: Die Anzahl der Nebenklassen multipliziert mit | H | ergibt | G | . Die Spalten sind genau die Teilungsreste bei der Division durch 3. Jetzt mag man versucht sein, hier nur mit den Nebenklassen zu rechnen, also modulo 3, und sich fragen, ob es so ein Konzept zu jeder Untergruppe für beliebige Gruppen gibt. Dies führt zur folgenden Definition: NormalteilerIst für jedes Element Ein Sonderfall ist: In einer abelschen Gruppe ist jede Untergruppe Normalteiler. FaktorgruppeDamit können wir nun unser Konzept des Rechnens auf den Nebenklassen umsetzen: Ist N ein Normalteiler, dann kann man auch nur mit den Nebenklassen rechnen und erhält eine Gruppe. Die Verknüpfung ist wie folgt gegeben: Diese Definition ist konsistent, da das Ergebnis von der Wahl der Elemente g und h aus den Nebenklassen unabhängig ist. Die mit dieser Verknüpfung und den Spalten (Nebenklassen) als Elementen definierte Gruppe nennt man die Faktorgruppe von G bezüglich H. Zyklische GruppenGibt es in G ein Element a, so dass man jedes andere Element als Potenz an (mit einer ganzen Zahl n, die auch negativ sein darf) schreiben kann, so nennt man G eine zyklische Gruppe und a erzeugendes Element. Klassifikation der endlichen einfachen GruppenEine nicht-triviale Gruppe heißt einfach, wenn sie keine Normalteiler außer der trivialen Gruppe und sich selbst hat. Beispielsweise sind alle Gruppen von Primzahlordnung einfach. Die einfachen Gruppen spielen eine wichtige Rolle als „Grundbausteine“ von Gruppen. Seit 1982 sind die endlichen einfachen Gruppen vollständig klassifiziert. Sie lassen sich in einer von 18 Familien endlicher einfacher Gruppen und 26 Ausnahmen, die sporadischen Gruppen einteilen. AusblickDie Eigenschaften endlicher Gruppen lassen sich mit dem Zauberwürfel veranschaulichen, der seit seiner Erfindung vielfach als Unterrichtsmittel im akademischen Unterricht Einsatz gefunden hat, weil die Permutationen der Ecken- und Kantenelemente des Würfels ein sichtbares und handgreifliches Beispiel einer Gruppe darstellen. Es gibt auch Verallgemeinerungen der Gruppentheorie. Eine Herangehensweise ist die Definition der Halbgruppen und Monoide: Für Halbgruppen wird nur die Assoziativität verlangt. Existiert in einer Halbgruppe ein neutrales Element, so spricht man von einem Monoid. Eine andere Verallgemeinerung stellen die Quasigruppen dar. Anwendung in der ChemieDie Chemie beschäftigt sich mit Molekülen. Die Koordinaten der Atome der Moleküle in ihrer Gleichgewichtskonformation lassen sich mit Hilfe von Symmetrieoperationen (Spiegelung, Drehung, Inversion, Drehspiegelung) auf sich selbst abbilden. Die Symmetrieoperationen haben die Eigenschaften von Gruppen, die sog. Punktgruppen. Außerdem kann gezeigt werden, dass die Gruppentheorie auch für die Symmetrie von Funktionen gilt, also auch für Wellenfunktionen in der Quantenmechanik. Beispielanwendungen aus der Chemie
Anwendung in der PhysikDie Symmetriegruppen der Kristalle werden selbstverständlich auch für die Festkörperphysik verwandt. Zudem baut die Quantenmechanik vielfach auf Symmetriegruppen und Lie-Gruppen auf. So werden die Elektronenspinzustände durch die Paulischen Spinmatrizen-Gruppe beschrieben. Auch in der Kernphysik werden gruppentheoretische Überlegungen zur Beschreibung des Kernaufbaus verwandt. In der Teilchenphysik und den Quantenfeldtheorien schließlich findet die Gruppentheorie Anwendung als Ordnungsschema. Siehe auch
|
|||||||||||
| Dieser Artikel basiert auf dem Artikel Gruppentheorie aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





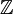 mit der Addition „+“ als Verknüpfung und der Null als neutralem Element, oder
mit der Addition „+“ als Verknüpfung und der Null als neutralem Element, oder
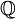 ohne Null mit der Multiplikation „ד als Verknüpfung und der Eins als neutralem Element. Die Null muss hierbei ausgeschlossen werden, da sie kein inverses Element besitzt. („1/0“ ist nicht definiert.)
ohne Null mit der Multiplikation „ד als Verknüpfung und der Eins als neutralem Element. Die Null muss hierbei ausgeschlossen werden, da sie kein inverses Element besitzt. („1/0“ ist nicht definiert.)
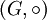 mit einer Menge
mit einer Menge 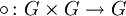 heißt Gruppe, wenn folgende Axiome erfüllt sind:
heißt Gruppe, wenn folgende Axiome erfüllt sind:
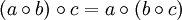
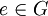 , mit dem für alle Gruppenelemente
, mit dem für alle Gruppenelemente 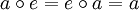
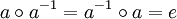
 symmetrisch ist, d. h. wenn zusätzlich das folgende Axiom erfüllt ist:
symmetrisch ist, d. h. wenn zusätzlich das folgende Axiom erfüllt ist:
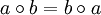 .
.
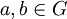 auch
auch 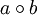 wieder in der Menge
wieder in der Menge  benutzt, man spricht dann von einer multiplikativ geschriebenen Gruppe. Das neutrale Element heißt dann auch Einselement und wird durch
benutzt, man spricht dann von einer multiplikativ geschriebenen Gruppe. Das neutrale Element heißt dann auch Einselement und wird durch 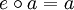 .
.
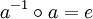 .
.
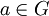 gilt:
gilt:
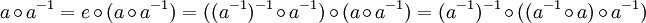
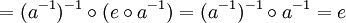
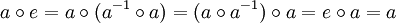
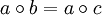 oder
oder 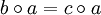 mit Gruppenelementen
mit Gruppenelementen 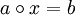 stets eindeutig lösbar mit Lösung
stets eindeutig lösbar mit Lösung 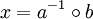 .
.
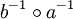 .
.
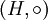 selbst eine Gruppe, so nennt man
selbst eine Gruppe, so nennt man 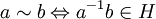 ,
,
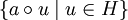
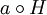 oder kurz
oder kurz 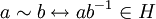 ,
,
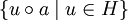 .
.
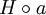 oder kurz
oder kurz