Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Teilchen im KastenDas Teilchen im Kasten ist eines der verschiedenen Modellsysteme aus der Quantenmechanik, welches zur Quantisierung der Energie führt. In diesem Artikel soll die Schrödinger-Gleichung für diesen Modellfall gelöst werden. Produkt-Highlight
Gedanklicher AufbauDas eindimensionale Modellsystem besteht aus einem freien Teilchen (beispielsweise einem Gasmolekül), welches zwischen zwei "Wänden" (eine bei x = 0 und eine bei x = L) eingesperrt ist. Im Inneren des Kastens herrscht ein Potential von Null. Die "Wände" symbolisieren eine unendlich hohe Potentialbarriere. Im Gegensatz zur klassischen Physik führt die quantenmechanische Beschreibung dieses Modells zu zwei wesentlichen Unterschieden:
Wenn die Potentialbarriere endlich ist, kommt ein dritter Unterschied hinzu. Ein quantenmechanisches Teilchen kann auch eine Potentialbarriere überwinden, für die es eigentlich nicht genügend Energie besitzt. Dies nennt man den Tunneleffekt. Die Lösungen der Schrödinger-Gleichung führen zur Quantisierung der EnergieWie bei einem freien Teilchen lautet die zeitunabhängige Schrödinger-Gleichung innerhalb des Kastens
Die Wellenfunktion ψ(x) lässt sich schreiben als und für die Energie E erhält man
Beschränkt werden die Lösungen allerdings durch die Randbedingung, dass die Wellenfunktion
Aus der ersten Randbedingung folgt
Damit diese Gleichung erfüllt wird, muss B = 0 sein. Damit vereinfacht sich die Wellenfunktion zu
Mit Hilfe der zweiten Randbedingung folgt dann
Damit diese Gleichung erfüllt wird, muss kL ein ganzes Vielfaches von π sein, also Löst man diesen Ausdruck nach k auf und setzt ihn in die Gleichung für die Energie E ein, so erhält man
Da n nur ganzzahlige Werte annehmen darf, kann die Energie ebenfalls nur bestimmte Werte annehmen. Die Energie des Teilchens ist somit gequantelt, die Energieniveaus sind „diskret“. Modell für konjugierte SystemeDas Teilchen im Kasten kann als einfaches Modell für ein konjugiertes Molekül, z.B. Hexatrien, verwendet werden, um dessen Energie abzuschätzen. Man nimmt an, dass sich die Elektronen in einem konjugierten Molekül in diesem frei bewegen können, aber es nicht verlassen können. Man Addiert formal ein halbes Atom an jedem Ende des Moleküls. Die Länge dieses Teilchens entspricht dann dem Kasten in dem sich das Elektron befindet. BeispieleEin Beispiel aus der Kristallographie ist das Farbzentrum, bei denen ein Elektron in einer Anionen-Leerstelle eingesperrt ist und das sich in guter Näherung als ein Teilchen im Kasten beschreiben lässt. Auch die Farbigkeit von Farbstoffen mit linearen konjugierten Pi-Systemen lässt sich erfassen, indem man das Pi-System als 1-dimensionales Teilchen im Kasten-Problem betrachtet. Siehe auchKategorien: Quantenphysik | Quantenmechanik | Quantenchemie | Theoretische Chemie |
|
| Dieser Artikel basiert auf dem Artikel Teilchen_im_Kasten aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




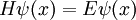 .
.
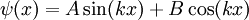
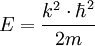 .
.
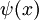 an den Wänden gleich 0 sein muss. Es muss also gelten
an den Wänden gleich 0 sein muss. Es muss also gelten
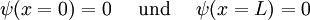 .
.
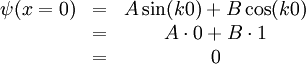 .
.
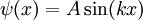 .
.
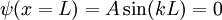 .
.
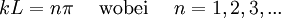
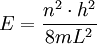 .
.


