Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Wannierdarstellung
Produkt-HighlightDie nach dem Schweizer Physiker Gregory Hugh Wannier benannte Wannierdarstellung ist in der Festkörperphysik beheimatet. In der Tight-Binding-Näherung ist eine Beschreibung der elektronischen Wellenfunktionen in der gitterperiodischen Bloch-Basis nicht mehr sinnvoll. Eher konstruiert man die Zustandsfunktion aus atomaren Wellenfunktionen. Diese sind aber nicht orthonormiert. Es lässt sich jedoch eine Ortonormal-Basis lokalisierter Zustände aus den Bloch-Funktionen konstruieren. Dabei ist Je größer die Gitterkonstante ist, desto stärker sind die Wannierzustände lokalisiert. Sie nähern sich immer mehr an die atomaren Zustände an. Statt aber den Wannierzustand einfach einem atomaren Zustand gleichzusetzen, nähert man ihn durch eine Linearkombination von atomaren Zuständen (LCAO): Die Menge U stellt dabei einen Unterraum der atomaren Zustände |
| Dieser Artikel basiert auf dem Artikel Wannierdarstellung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




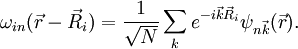
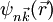 eine
eine 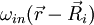 der zugehörige Wannier-Zustand. Die umgekehrte Konstruktion der Blochzustände aus den Wannierzuständen heißt dann
der zugehörige Wannier-Zustand. Die umgekehrte Konstruktion der Blochzustände aus den Wannierzuständen heißt dann
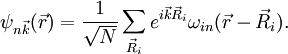
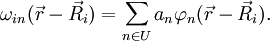
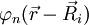 dar.
dar.


