Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Bloch-FunktionDie Bloch-Funktion oder Bloch-Welle (nach Felix Bloch) ist die allgemeinste Lösung der stationären Schrödingergleichung für ein x0-periodisches Potential (z.B. die Wellenfunktion eines Elektrons in einem kristallinen Festkörper). Die Form dieser Wellenfunktionen wird durch das Bloch-Theorem festgelegt:
Die Periodizität des Potentials V(x)=V(x+x0) überträgt sich also auf uk(x) und damit auf die Aufenthaltswahrscheinlichkeit des betrachteten Teilchens |ψ|2 im Potential. Betrachtet man einen kristallinen Festkörper, so ist die Periodizität x0 durch das Kristallgitter, also einen Gittervektor gegeben.
Kurze HerleitungDas Potential V(r) ist invariant gegenüber einer Translation um einen Vektor R (in einem Kristall ist R ein Gittervektor):
Diese Bedingungen werden aber gerade durch die Bloch-Funktion erfüllt.
Literatur
Kategorien: Quantenmechanik | Festkörperphysik |
|
| Dieser Artikel basiert auf dem Artikel Bloch-Funktion aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


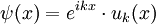


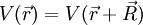
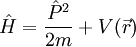 des Teilchens. Daher unterscheiden sich zwei
des Teilchens. Daher unterscheiden sich zwei 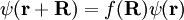 .
.
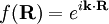 .
.


