Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
SuperpositionsprinzipWeiteres empfehlenswertes Fachwissen
MathematikIn der Mathematik bedeutet das Superpositionsprinzip, dass eine Linearkombination von Lösungen einer homogenen linearen Gleichung wieder eine Lösung dieser Gleichung ist. Beispielsweise kann man bei einer homogenen linearen Differentialgleichung Lösungen
mit beliebigen Koeffizienten. Dies wird als Superposition oder Superpositionsprinzip bezeichnet. Das gleiche gilt für Lösungen von homogenen partiellen Differentialgleichungen. PhysikMechanikWirken auf einen Punkt (oder einen starren Körper) mehrere Kräfte Weiterhin gilt das obige mathematische Superpositionsprinzip für lineare Kräfte und Spannungen, insbesondere auch für harmonische Oszillatoren. WellenDas Superpositionsprinzip bedeutet hier, dass Wellen sich überlagern können, ohne sich gegenseitig zu beeinflussen. Die resultierende Welle kann für jeden Ort als Funktion (meist als Summe) der verursachenden Wellen angegeben werden. Im Bereich der linearen Optik gilt dieses Prinzip weitgehend. Hier überlagern sich elektromagnetische Wellen, ohne sich zu beeinflussen: Eine Welle breitet sich in einem Medium in immer gleicher Weise aus – unabhängig von eventuell vorhandenen weiteren Wellen. Lineare Überlagerung ist auch bei kleinen Wasserwellen zu beobachten: Einzelne Wellenzüge überlagern sich in einem Wechselwirkungsgebiet linear und laufen nach Verlassen dieses Gebietes in ihrer ursprünglichen Form weiter. Im Bereich der nichtlinearen Optik hingegen kommt es zu Energieübertragungen zwischen den wechselwirkenden Primärwellenzügen. Daraus resultieren Amplituden- und Frequenzänderungen sowie eine Neuausbildung von sekundären elektromagnetischen Wellen. Die resultierende Welle ist hier nicht mehr einfach aus der Superposition der verursachenden Wellen angebbar. Analog geht bei großen Wasserwellen die Superpositionierbarkeit der Elementarwellen verloren. Die resultierende Amplitude wird durch Überlagerung so groß, dass die Welle „bricht“. WärmelehreDas Superpositionsprinzip wird beispielsweise angewandt zur Berechnung von transienten Erwärmungsvorgängen. Man kann die Temperatur beispielsweise eines Leistungshalbleiters zu einem gewissen Zeitpunkt t bestimmen in Abhängigkeit von Leistungsimpulsen über die Zeit. Im nebenstehenden Beispiel wirkt vom Zeitpunkt t = 0 bis t = t1 eine Leistung. Die Temperatur steigt nach einer e-Funktion an: Um nun die Temperatur zu einem Zeitpunkt zu ermitteln, lässt man den Leistungspuls fortwirken und setzt beim Erwärmungsende einen gleich großen negativen Leistungsimpuls an. Daraus resultiert eine "negative Erwärmungskurve" (grüne Kurve). Die Summe der beiden Erwärmungskurven ergibt die Abkühlfunktion (blaue Kurve). QuantentheorieIn der Quantentheorie gilt das Superpositionsprinzip sehr allgemein und exakt für abgeschlossene Systeme (die per Definition nicht mit ihrer „Umgebung“ verschränkt sind). Das bedeutet erstens, dass sich zwei beliebige Zustände (zu einer bestimmten Zeit) mit beliebigen komplexen Koeffizienten superponieren lassen und dadurch einen neuen möglichen Zustand definieren, und zweitens, dass sie bereits eine neue Lösung der Schrödingergleichung bilden, wenn sie einzeln als solche Lösungen in der Zeit fortgesetzt werden. Beispielsweise bildet die Superposition aller möglichen Positionen eines "Massenpunktes" eine Wellenfunktion im Raum, wobei verschiedene Wellenfunktionen sich wiederum superponieren lassen. Jedoch sind quantenmechanische Superpositionen allgemein im Konfigurationsraum definiert (also nichtlokal). ElektrotechnikIn der Elektrotechnik bildet das Superpositionsprinzip, auch bekannt als Überlagerungssatz, die Grundlage aller numerischen Methoden, die bei der Netzwerkanalyse zur Simulation von linearen und nichtlinearen Schaltungen im Zeit- und Frequenzbereich Anwendung finden. Entsprechend den Kirchhoffschen Regeln bildet die Summe aller in einen Knoten einfließenden Ströme den herausfließenden Strom (Knotenregel), die Summe aller Teilspannungen die Gesamtspannung über einem Zweig (zu einem Zeitpunkt) (Maschenregel). AnwendungsregelIn einem linearen Netzwerk aus Bauelementen und Quellen lassen sich Spannungen und Ströme durch Überlagerung von Teillösungen berechnen. Hierzu werden alle Quellen bis auf eine zu Null gesetzt. Die Leitung wird bei Spannungsquellen kurzgeschlossen, bei Stromquellen aufgetrennt. Jetzt kann für jede einzelne Quelle die vollständige Schaltung berechnet werden. Anschließend werden alle Teilergebnisse, unter Beachtung der Vorzeichen, addiert. Die Summe ist das Ergebnis des realen Netzwerks. |
|
| Dieser Artikel basiert auf dem Artikel Superpositionsprinzip aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





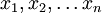 durch Summation zu einer neuen Lösung zusammensetzen:
durch Summation zu einer neuen Lösung zusammensetzen:
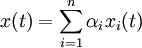
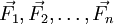 , so addieren sich diese vektoriell zu einer resultierenden Kraft
, so addieren sich diese vektoriell zu einer resultierenden Kraft 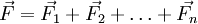 auf. Dies nennt man Superpositions- oder auch Überlagerungsprinzip der Kräfte.
auf. Dies nennt man Superpositions- oder auch Überlagerungsprinzip der Kräfte.
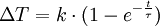 (rote Kurve)
(rote Kurve)


