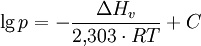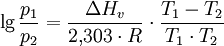Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Clausius-Clapeyron-GleichungDie Clausius-Clapeyron-Gleichung wurde 1834 von Benoit Clapeyron entwickelt und später von Rudolf Clausius aus den Theorien der Thermodynamik abgeleitet. Sie ist eine Spezialform der Clapeyron-Gleichung. Produkt-HighlightÜber sie lässt sich der Verlauf der Phasengrenzlinie eines Phasendiagramms zwischen der flüssigen und der gasförmigen Phase eines Stoffes, der Siedepunktskurve, errechnen. Die thermodynamisch korrekte Version der Gleichung ist Allerdings bezeichnet man im Regelfall die näherungsweise gültige Gleichung: als Clausius-Clapeyron-Gleichung. Hier wurde in guter Näherung Anwendung auf ideale GaseBetrachtet man über einen kleinen Temperaturbereich die Verdampfungsenthalpie eines Stoffes als konstant, so hängen der Dampfdruck p und die Temperatur T wie folgt zusammen: bzw. (wegen Um nun den Sättigungsdampfdruck p1 einer Flüssigkeit bei einer Temperatur T1 mit dem Sättigungsdampfdruck p2 der gleichen Flüssigkeit bei einer Temperatur T2 zu vergleichen, verwendet man die Clausius-Clapeyron-Gleichung in folgender Form: |
| Dieser Artikel basiert auf dem Artikel Clausius-Clapeyron-Gleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





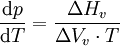
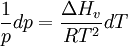
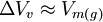 gesetzt, da das Molvolumen eines Gases viel größer als das einer Flüssigkeit ist, und es wurde ein ideales Gas angenommen, für das gilt:
gesetzt, da das Molvolumen eines Gases viel größer als das einer Flüssigkeit ist, und es wurde ein ideales Gas angenommen, für das gilt:
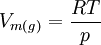
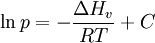
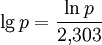 )
)