Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
SättigungsdampfdruckDer Sättigungsdampfdruck beschreibt den bei einer bestimmten Temperatur maximalen Dampfdruck. Man spricht in diesem Fall von einer Sättigung des Gases. Üblicherweise wird der Sättigungsdampfdruck in der Chemie mit „Dampfdruck“ abgekürzt, worauf jedoch im Folgenden aus Gründen der Eindeutigkeit verzichtet wird. Aus reinen Flüssigkeiten oder reinen Festkörpern entweichen solange Atome/Moleküle in die Gasphase, bis sich darin ein von der Stoffart, dessen vorliegender Phase und der Gleichgewichtstemperatur abhängiger Druck eingestellt hat. Dieser Druck ist der Sättigungsdampfdruck. Er herrscht, wenn das Gas im thermodynamischen Gleichgewicht (identische chemische Potenziale der Phasen) mit der Flüssigkeit bzw. dem Feststoff steht. In diesem Zustand ist also die Verdampfung bzw. Sublimation der Flüssigkeit bzw. des Feststoffes mengenmäßig gleich der Kondensation bzw. Resublimation des Gases. Keine der Phasen wächst unter dem Strich auf Kosten der anderen, wodurch beide nebeneinander stabil existieren können. Man spricht daher auch von einem dynamischen Gleichgewicht. Weitere übliche Definitionsweise: Der Sättigungsdampfdruck ist eine Eigenschaft eines Feststoffes oder einer Flüssigkeit. Er ist ein Maß für den Anteil derjenigen Moleküle oder Atome, die genügend Energie haben die Nah- und Fernordnung (Kohäsionskräfte, Oberflächenspannung) zu überwinden und in die gasförmige Phase zu wechseln (Phasenübergang). Da die Geschwindigkeitsverteilung, zum Beispiel die Maxwell-Boltzmann-Verteilung, eine exponentielle Funktion ist, zeigt auch die Dampfdruckkurve exponentielles Verhalten als Funktion der Temperatur. Produkt-Highlight
Formelzeichen und EinheitFür den Sättigungsdampfdruck wird meist das Formelzeichen E verwandt, es sind jedoch auch weitere Formen wie es und ps, max, für flüssiges Wasser speziell ew und pw, max sowie für Eis ei und pi, max gebräuchlich. Die jeweiligen Indizes finden sich auch beim groß geschriebenen E. Je nach Anwendungsgebiet werden unterschiedliche Druckeinheiten genutzt, wobei in den Naturwissenschaften Hektopascal (hPa) und Megapascal (MPa), in den Ingenieurswissenschaften hingegen Bar (bar) am gebräuchlichsten sind. Der Sättigungsdampfdruck im PhasendiagrammIm Phasendiagramm ist der Sättigungsdampfdruck nichts anderes als der Wert des Druckes entlang der hier als schwarz gekennzeichneten Phasengrenzlinie zwischen der Gasphase und der korrespondierenden festen bzw. flüssigen Phase. Diese Phasengrenzlinie wird daher auch als Dampfdruckkurve oder Sättigungsdampfdruckkurve bezeichnet. Für das Phasengleichgewicht Gas-Festkörper heißt der Sättigungsdampfdruck auch Sublimationsdruck und für das Phasengleichgewicht Gas-Flüssigkeit auch Siededruck. Zu beachten ist hierbei, dass bei Temperaturen über dem kritischen Punkt keine flüssige Phase und somit auch kein Sättigungsdampfdruck mehr existiert. Des Weiteren spielt die Phasengrenzlinie zwischen Feststoff und Flüssigkeit, die so genannte Schmelzkurve, keine Rolle für den Sättigungsdampfdruck. Anwendungen und BedeutungDer Sättigungsdampfdruck steigt exponentiell mit der Temperatur an. Die Teilchenzahl eines spezifischen Gasvolumens ist im Gleichgewichtszustand also bei höheren Temperaturen größer als bei niedrigeren Temperaturen, was auch gleichbedeutend zu einer mit der Temperatur ansteigenden Teilchendichte ist. Wichtige Beispiele sind Wasserdampf und Luftfeuchtigkeit. Viele Feuchtemaße werden über Dampfdruck und Sättigungsdampfdruck definiert und/oder berechnet, besonders im Zusammenhang der relativen Luftfeuchtigkeit, des Sättigungsdefizits und des Taupunkts. Die mit dem Sättigungsdampfdruck beschriebenen thermodynamischen Eigenschaften sind von größter Bedeutung und finden auch in nahezu allen naturwissenschaftlichen und technischen Disziplinen eine mannigfaltige Verwendung, wobei hier Wasser zwar den wichtigsten Stoff darstellt, diese Anwendungen jedoch auch keineswegs auf Wasser beschränkt bleiben. Besonders bedeutungsvoll sind hierbei die Effekte (siehe unten) einer realen Umgebung auf den theoretisch hergeleiteten Sättigungsdampfdruck, da sich hieraus viele für die Meteorologie aber auch für technische Anwendungen wichtige Erkenntnisse und Anwendungen ableiten. Ein Beispiel für eine Anwendung des Sättigungsdampfdruckes in der Technik ist die Gefriertrocknung, ein weiteres die Druckkochung, siehe Schnellkochtopf. MessungZur Messung des Sättigungsdampfdrucks ist es nötig die entsprechende Flüssigkeit bzw. den Feststoff in reiner Form in ein geschlossenes Gefäß zu füllen und danach mit einer Vakuumpumpe die Luft zu evakuieren. Solange die flüssige bzw. feste Phase weiterhin vorhanden ist, wird sich hiernach automatisch der Sättigungsdampfdruck in Abhängigkeit von der jeweiligen Temperatur einstellen. Da die Gasphase des Stoffes in reiner Form vorliegt, kann man den Sättigungsdampfdruck mit einem hinreichend genauen Manometer messen. Berechnung und EinflussfaktorenFür die Berechnung des Sättigungsdampfdruckes kann man die Clapeyron-Gleichung bzw. speziell für den Phasenübergang flüssig-gasförmig auch die Clausius-Clapeyron-Gleichung nutzen. In Anwendung auf den Sättigungsdampfdruck lautet diese: Die einzelnen Formelzeichen stehen für folgende Größen:
Im Falle des für viele Anwendungen sehr wichtigen Sättigungsdampfdruckes des Wassers hat man daher verschiedene Näherungsgleichungen entwickelt, deren einfachster Typ die Magnus-Formeln sind. Die derzeit exakteste Gleichung zur Berechnung des Dampfdruckes über Wasser ist die Goff-Gratch-Gleichung - ein Polynom sechsten Grades in Logarithmen der Temperatur - die auch von der WMO empfohlen wird.
Berechnung des Sättigungsdampfdrucks von Wasser über die Magnus-FormelDer Sättigungsdampfdruck für Wasserdampf kann mit Hilfe der Magnus-Formel (hier nach Sonntag 1982) berechnet werden. Über ebenen Wasseroberflächenoder wobei gilt: Über ebenen Eisoberflächenoder wobei gilt: HinweiseDatentabelle mit genaueren Formeln. In den Magnus-Formeln ist zu beachten, dass für t die Temperatur in Grad Celsius und nicht in Kelvin einzutragen ist. Der sich ergebende Sättigungsdampfdruck hat die Einheit des Vorfaktors E0(t), also bei dem hier angegebenen Werten hPa. Jenseits von auf der Erde natürlich auftretenden Temperaturwerten kann die Abweichung der empirisch ermittelten Magnus-Formel zum realen Wert stark zunehmen, weshalb man sich auf die angegebenen Temperaturbereiche beschränken sollte. Die Magnus-Formeln gelten nur für ebene Oberflächen und auch hier nur für reines Wasser. Ihr Fehler ist jedoch vergleichsweise recht groß, so dass diese beiden Effekte bei einer geringen Ausprägung meist vernachlässigbar sind. Die Standardabweichung der Ergebnisse beträgt beidseitig bis zu einem halben Prozent. Bei gekrümmten Oberflächen, beispielsweise bei kugelförmigen Tröpfchen, ist der Sättigungsdampfdruck höher (Krümmungseffekt siehe unten), hingegen bei salzhaltigen Lösungen geringer (Lösungseffekt siehe unten). Diese beiden modifizierenden Einflüsse spielen eine wesentliche Rolle bei der Bildung von Niederschlagsteilchen. Im Laborexperiment kann Kondensation über einer ebenen Fläche mit destilliertem Wasser und einer sehr reinen Luft erst nach Übersättigungen von mehreren hundert Prozent erreicht werden. In der realen Atmosphäre spielen hingegen Aerosole eine wesentliche Rolle als Kondensationskeime. Dies hat zur Folge, dass man in der Realität selten Übersättigungen von mehr als einem Prozent beobachtet. Zum Vergleich der Magnus-Formel mit einer anderen Darstellungsform ist der Artikel Wasserdampf zu empfehlen. Die Magnus-Formel wurde erstmals 1844 von Heinrich Gustav Magnus aufgestellt und seitdem lediglich durch genauere Werte ergänzt, wobei die hier genutzten Werte aus D. Sonntag (1982) stammen. Eine genauere Berechnung, sowie viele Beispielwerte, finden sich im nächsten Abschnitt. EffekteIm Gegensatz zum durch die obigen Gleichungen beschriebenen Idealfall eines Reinstoffes und einer ebenen Oberfläche zeigen sich in der Realität weitere Einflussfaktoren, welche den letztendlichen Sättigungsdampfdruck mitbestimmen. Krümmungs- und LösungseffektBei Bildung von Flüssigkeitspartikel an Kondensationskernen tritt der Krümmungseffekt auf. Es zeigt sich dabei, dass über den gekrümmten Oberflächen der entstehenden Flüssigkeitstropfen ein höherer Sättigungsdampfdruck auftritt, als im Vergleich zu einer planaren Wasseroberfläche. Liegt die Flüssigkeit bei einer Änderung des Aggregatzustands nicht als Reinstoff vor, so muss man auch den Lösungseffekt beachten. Die in der Flüssigkeit gelösten Teilchen erschweren es hierbei den Flüssigkeitsverbund zu verlassen, weshalb der Sättigungsdampfdruck niedriger ist, als bei einer reinen Flüssigkeit der Fall wäre. Unter atmosphärischen Bedingungen treten beide Effekte meist gemeinsam auf und eine alleinstehende Betrachtung ist wenig zielführend. LadungseffektAuch die elektrische Ladung der Oberfläche hat eine Auswirkung auf den Sättigungsdampfdruck, welche jedoch im Vergleich zu den anderen Effekten minimal ist und daher keine praktische Rolle spielt. Korrekturfaktoren für feuchte LuftDie Korrekturfaktoren (engl.: enhancement factor) sind nötig, da der Wasserdampf nicht in reiner Form vorliegt, sondern innerhalb der feuchten Luft. Sie gelten lediglich bei einem Luftdruck von 1013,25 hPa (Normaldruck). Bei höheren Drücken sind sie größer und dementsprechend bei niedrigeren Drücken kleiner.
Da die Korrekturfaktoren temperaturabhängig sind und in den obigen Werten recht große Temperaturintervalle umfassen, stellen sie nur recht grobe Näherungen an die tatsächliche Abweichung dar. Die negativen Temperaturen über Wasser beziehen sich auf unterkühltes Wasser. Um die resultierenden Werte für den Sättigungsdampfdruck zu erhalten, gilt:
Zusammenhang mit der SättigungsmengeNach der allgemeinen Gasgleichung ist der Sättigungsdampfdruck (näherungsweise) auch das Produkt der Sättigungsmenge mit der individuellen Gaskonstante und der Temperatur (in Kelvin), als Formel etwa: – vgl. Dampfdruck bzw. Sättigung.
Neben der Bezeichnung Sättigungsmenge findet man auch Sättigungskonzentration und Sättigungs-(dampf-)dichte (Titel von Sonntag 1982), die SI-Einheit ist zumeist g/m3. Bei Wasserdampf spricht man auch von der maximalen Luftfeuchte. Literatur
Siehe auchKategorie:Sättigungsdampfdruckgleichungen Kategorien: Thermodynamik | Stoffeigenschaft |
|
| Dieser Artikel basiert auf dem Artikel Sättigungsdampfdruck aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





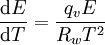
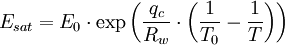
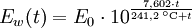
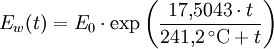
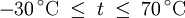
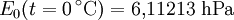
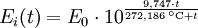
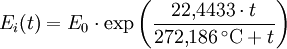
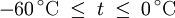
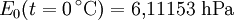
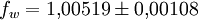
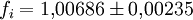
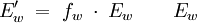 - Tabellenwert
- Tabellenwert
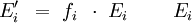 - Tabellenwert
- Tabellenwert



