Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Dember-EffektAls Dember Effekt bezeichnet man die Erzeugung elektrischer Spannung bei Lichteinfall auf bestimmte Kristalle. Er wurde nach seinem Entdecker Harry Dember benannt. Produkt-Highlight
BeschreibungBei Belichtung eines Halbleiters mit Licht aus dem Wellenlängenbereich der Grundgitterabsorption entsteht ein elektrisches Feld in Lichtausbreitungsrichtung. An geeignet angebrachten Kontakten kann eine elektrische Spannung abgegriffen werden. Dieser Effekt wurde zuerst von Harry Dember 1931 an Kupfer(I)-oxid beobachtet. Diese longitudinale Demberspannung lässt sich experimentell nur sehr schwer bestimmen, weil sie von Sperrschicht-Photoeffekten an Potentialbarrieren an Metall-Halbleiter-Kontakten bzw. der freien Halbleiteroberfläche, die wesentlich größer sind als der Dember-Effekt, überlagert wird. Der Effekt spielte technisch bisher keine Rolle, ist aber für das Verständnis des Verhaltens von Nichtgleichgewichtsträgern in Halbleiterstrukturen von grundlegender Bedeutung. Mittlerweile gewinnt der Effekt u.U. an größerer Bedeutung für die Erzeugung von Strahlung im Terahertz-Regime. SachverhaltIn homogenen Halbleitern entstehen Photospannungen, wenn Überschussladungsträger mit unterschiedlichen Beweglichkeiten unter dem Einfluss von Ladungsträgergradienten diffundieren. Abbildung 1 zeigt schematisch die Entstehung des longitudinalen Dember-Effektes. In Halbleitern, in denen die Diffusionslänge der Nichtgleichgewichtsträger wesentlich gößer ist als die Debye-Länge, herrscht annähernd Raumladungsfreiheit. Wird Licht aus dem Wellenlängengebiet der Grundgitterabsorption des Halbleiters eingestrahlt, werden die Nichtgleichgewichtsträger(δn: Elektronen, δp Löcher) nahe der Probenoberfläche erzeugt und diffundieren in Richtung der Konzentrationsgradienten ins Probeninnere. Sind Elektronenbeweglichkeit μn und Löcherbeweglichkeit μp unterschiedlich, wird die Raumladungsfreiheit δn = δp und (bei offenem Stromkreis) das Verschwinden des elektrischen Stromes in der Probe dadurch erzwungen, daß sich ein inneres elektrisches Feld EZ aufbaut, das so gerichtet ist, daß es die langsamer diffundierenden Ladungsträger beschleunigt, die anderen bremst. EZ sorgt dafür, daß sich Elektronen und Löcher mit gleicher Geschwindigkeit bewegen. Es fließt ein Teilchenstrom in z-Richtung, während der elektrische Strom verschwindet (ambipolare Diffusion). Die ambipolare Diffusion spielt nicht nur bei optisch erzeugten Nichtgleichgewichtsträgergradienten eine Rolle, sondern in allen Fällen, in denen solche Gradienten bei Ladungsträgerinjektion bzw. verstärkter Rekombination an Oberflächen oder inneren Grenzflächen entstehen. In Halbleitern mit anisotroper elektrischer Leitfähigkeit entsteht bei Lichteinstrahlung auf eine geeignet orientierte Probe zusätzlich ein elektrisches Feld EX senkrecht zur Einstrahlungsrichtung (Abb. 2). In anisotropen Halbleitern sind die Diffusions- und Driftströme im allgemeinen nicht in Richtung der Konzentrationsgradienten bzw. elektrische Felder gerichtet. Um auch die x-Komponente der Diffusionsströme zu kompensieren, baut sich neben dem longitudinalen das transversale Dember-Feld EX auf. Die Messung der transversalen Dember-Spannung bietet keine Schwierigkeiten, da Störeffekte vermieden werden können, indem man die Kontakte in hinreichendem Abstand vom belichteten Gebiet anbringt. Der transversale Dember-Effekt tritt an natürlich anistropen Substanzen, wie z.B. Tellur, auf bzw. an Substanzen, die unter dem Einfluss äußerer Einwirkungen anisotrop werden. Hier sind besonders die kubischen Vieltalhalbleiter, wie z.B. n-Germanium, n-Silizium, PbTe (Altait), von Interesse, die bei ungleicher Besetzung der Energietäler mit Ladungsträgern anistrop werden. Dies tritt ein, wenn durch uniaxialen Druck die Äquivalenz der Täler aufgehoben wird oder linear polarisierte Strahlung in den Tälern unterschiedlich stark absorbiert wird. Kennwerte, FunktionenFür den longitudinalen Dember-Effekt gilt
Hier sind mn, mp die Beweglichkeiten der Elektronen und Löcher n0, p0 die Konzentrationen der Elektronen und Löcher im thermischen Gleichgewicht, dn(0), dn(d) die Konzentration der optisch erzeugten Überschusselektronen an der belichteten bzw. rückseitigen Oberfläche der Halbleiterprobe.
Auch das transversale Dember-Feld wird durch die Konzentration der Nichtgleichgewichtsträger an der Probenoberfläche und die Differenzen der Komponenten des Beweglichkeitstensor Der transversale Dember-Effekt in den Bleichalkogeniden zeigt eine charakteristische Abhängigkeit von der Polarisationsrichtung der Lichtwelle. Abbildung 3 zeigt das transversale Dember-Feld in PbTe. AnwendungenDie Spannungsempfindlichkeit des Dember Effektes ist geringer als Quellen
|
|
| Dieser Artikel basiert auf dem Artikel Dember-Effekt aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




![U=\dfrac{KT}{e} \dfrac{(\mu_n-\mu_p)}{n_0\mu_n+p_0\mu_p}[\delta n(0)-\delta n(d)]](images/math/8/9/f/89f9030b67a37263fd23316ba0a3da70.png) .
.
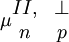 bestimmt. II und
bestimmt. II und 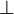 bezeichnen die Richtungen parallel und senkrecht zur Rotationsachse eines Energieellipsoids.
bezeichnen die Richtungen parallel und senkrecht zur Rotationsachse eines Energieellipsoids.
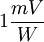 und damit wesentlich kleiner als die meisten anderen Photoeffekte im Halbleiter. Wegen der Störeffekte wird der longitudinale Effekt überhaupt nicht genutzt. Da der transversale Effekt in genau der gleichen Weise von der Konzentration der Nichtgleichgewichtsträger abhängt wie der photoelektromagnetische Effekt, ist das Verhältnis beider Effekte unabhängig von der Lebensdauer der Nichtgleichgewichtsträger, der optischen Generationsrate, Reflexionskoeffizienten der Probe usw. und kann zur Beweglichkeitsbestimmung genutzt werden.
Der transversale Dember-Effekt in den Vieltalhalbleitern bietet die Möglichkeit der Bestimmung der Zwischentalstreuzeit. Darüber hinaus kann die empfindliche Polarisationsabhängigkeit des Effektes zum Nachweis linear polarisierter Strahlung eingesetzt werden.
und damit wesentlich kleiner als die meisten anderen Photoeffekte im Halbleiter. Wegen der Störeffekte wird der longitudinale Effekt überhaupt nicht genutzt. Da der transversale Effekt in genau der gleichen Weise von der Konzentration der Nichtgleichgewichtsträger abhängt wie der photoelektromagnetische Effekt, ist das Verhältnis beider Effekte unabhängig von der Lebensdauer der Nichtgleichgewichtsträger, der optischen Generationsrate, Reflexionskoeffizienten der Probe usw. und kann zur Beweglichkeitsbestimmung genutzt werden.
Der transversale Dember-Effekt in den Vieltalhalbleitern bietet die Möglichkeit der Bestimmung der Zwischentalstreuzeit. Darüber hinaus kann die empfindliche Polarisationsabhängigkeit des Effektes zum Nachweis linear polarisierter Strahlung eingesetzt werden.


