Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Einstein-ModellIn der Festkörperphysik beschreibt das Einstein-Modell (nach Albert Einstein) eine Methode, um den Beitrag der Gitterschwingungen (Phononen) zur Wärmekapazität eines kristallinen Festkörpers zu berechnen. Es ist dabei nicht so erfolgreich wie das Debye-Modell. Produkt-Highlight
Grundlagen des ModellsDie Gitterschwingungen des Kristalls werden gequantelt, d.h. der Festkörper kann Schwingungsenergie nur in diskreten Quanten Damit ergibt sich die innere Energie U im Festkörper zu (Es wurde die Quantisierungsbedingung des harmonischen Oszillators verwendet): Der Beitrag Mit der Einstein-Temperatur Ergebnisse des ModellsEs ergibt sich im Limes großer bzw. kleiner Temperaturen: Wie das Debye-Modell liefert das Einstein-Modell das korrekte Hochtemperaturlimit nach dem Dulong-Petit-Gesetz. Der oben beschriebene Verlauf von CV(T) für kleine Temperaturen weicht allerdings erheblich von Messungen ab. Dies hängt mit der Annahme zusammen, alle harmonischen Oszillatoren im Festkörper würden mit einer einheitlichen Frequenz schwingen. Die Verhältnisse im realen Festkörper sind deutlich komplizierter. |
| Dieser Artikel basiert auf dem Artikel Einstein-Modell aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





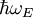 aufnehmen. Diese Quanten nennt man auch
aufnehmen. Diese Quanten nennt man auch 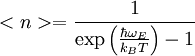
![U=3N\cdot\hbar\omega_E\cdot \left(<n>+\frac{1}{2}\right)= 3N\cdot\hbar\omega_E\cdot\left[\frac{1}{\exp\left(\frac{\hbar\omega_E}{k_BT}\right)-1}+\frac{1}{2}\right]](images/math/8/e/1/8e17c636219596461ec5ae4fd3a72a8c.png)
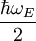 gibt die Nullpunktsenergie an. Der Beitrag der Phononen zur Wärmekapazität ist dann:
gibt die Nullpunktsenergie an. Der Beitrag der Phononen zur Wärmekapazität ist dann:
![C_V=\left(\frac{\partial U}{\partial T}\right)_{V={\rm const}}=\frac{3N}{k_BT^2}\frac{(\hbar\omega_E)^2}{\left[\exp\left(\frac{\hbar\omega_E}{k_BT}\right)-1\right]^2}\cdot\exp\left(\frac{\hbar\omega_E}{k_BT}\right)](images/math/d/f/9/df9a7a880b0afb8e00f193470642609d.png)
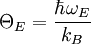 ergibt sich eine einfachere Schreibweise:
ergibt sich eine einfachere Schreibweise:
![C_V^{\rm mol}\left(T\right)=3R\cdot\left(\frac{\Theta_E}{T}\right)^2\cdot\frac{\exp\left(\frac{\Theta_E}{T}\right)}{\left[\exp\left(\frac{\Theta_E}{T}\right)-1\right]^2}](images/math/8/1/b/81b5a5f2ded8ae8d4576528ee3f91037.png)



