Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Phonon
Produkt-HighlightMan unterscheidet zwischen akustischen und optischen Phononen. Akustische Phononen (auch als Schallquanten bezeichnet) entsprechen weitestgehend den Schallwellen, die sich durch das Kristallgitter fortpflanzen. Hierbei bewegen sich alle Atome einer Einheitszelle in Phase, während sich die Atome einer Einheitszelle bei optischen Phononen gegenphasig bewegen. Sind die gegenphasig schwingenden Atome geladen, so existieren Schwingungsmodi, bei denen entgegengesetzt geladene Untergitter gegeneinander schwingen. Die dabei oszillierenden Dipolmomente können mit Photonen wechselwirken (daher die Bezeichnung optisches Phonon). Solche Kopplungen finden in der Regel im Infrarotbereich statt, also bei Wärmebewegungen innerhalb von Festkörpern. Man nennt solche Kristalle dann infrarot-aktiv. Beispiele für solche Gitter sind Ionengitter, zum Beispiel in Natriumchloridkristallen. In einem dreidimensionalen Kristall mit N Atomen in der Einheitszelle existieren zu jedem mit der Kristallsymmetrie verträglichen Wellenvektor 3N mögliche Schwingungsmoden: 3 akustische (davon eine longitudinal und zwei transversale) und 3(N − 1) optische. Der Zusammenhang zwischen Frequenz und Wellenvektor ist durch die Phononendispersion gegeben. Die Energiezustände εn der Phononen berechnen sich aus denen des harmonischen Oszillators nach
Da Phononen zu den Bosonen zählen, berechnet sich die mittlere Besetzungszahl
Das chemische Potential μ taucht in der Formel nicht auf, weil die Teilchenzahl der Phononen keine Erhaltungsgröße ist. Experimentell lassen sich die optischen Phononen mittels Raman-Spektroskopie oder Infrarot-Spektroskopie bestimmen. Zur Ermittlung des Gesamtspektrums der Phononen wird sowohl die Information über die Energie als auch über den Impuls der Gitterschwingungen benötigt. Diese Forderung wird durch die Neutronenstreuung, die Röntgenstreuung sowie durch die hochaufgelöste Elektronenenergieverlust-Spektroskopie (HREELS) erfüllt. Das Modell der Gitterschwingungen setzt eine kristalline Ordnung des Festkörpers voraus. Auch amorphe, also nicht kristallin geordnete, Festkörper wie Gläser zeigen Schwingungen der Elementarteilchen untereinander, man bezeichnet diese aber nicht als Phononen. Üblicherweise werden (wie oben) statistische Gemische von Zuständen mit bestimmter Phononenzahl (Fock-Zustände) verwendet. Wie Roy J. Glauber für Photonen 1963 zeigte, gibt es aber auch so genannte kohärente Zustände mit unbestimmter Teilchenzahl, bei Phononen also mit unbestimmter Phononenzahl. Diese ähneln sehr stark klassischen Gitterschwingungen. Während bei Fock-Zuständen der Erwartungswert der Auslenkung 0 ist, genügt er bei kohärenten Phononen-Zuständen der klassischen Zeitabhängigkeit von Gitterschwingungen. Der Begriff Phonon wurde in Analogie zu den Schwingungsquanten des elektromagnetischen Feldes, den Photonen gewählt und zum ersten Mal von Jakow Iljitsch Frenkel (1894–1952) 1932 in seinem Buch „Wave Mechanics, Elementary Theory“ verwendet. Kategorien: Festkörperphysik | Quantenphysik |
| Dieser Artikel basiert auf dem Artikel Phonon aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




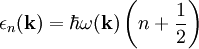 .
.
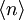 im thermischen Gleichgewicht gemäß der
im thermischen Gleichgewicht gemäß der 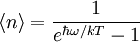 .
.


