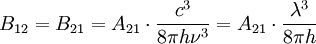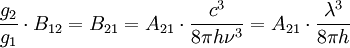Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
EinsteinkoeffizientenDie Einsteinkoeffizienten werden zur Berechnung der spontanen und induzierten Emission in der statistischen Physik verwendet und finden in der Lasertechnik Anwendung. Diese wurden 1917 von Albert Einstein eingeführt. Produkt-HighlightUm zu berechnen, wie viele Teilchen pro Zeit in einem 2-Niveausystem von einem Energiezustand N2 in den energetisch tieferen Zustand N1 "fallen", benutzt man folgende Formel:
wobei
Der 1. Term steht für die induzierte Absorption: Der 2. Term steht für die induzierte Emission: Der 3. Term steht für den spontanen Zerfall:
Im thermodynamischen Gleichgewicht sind die "Sprünge" Daraus folgt, dass Zwischen den 3 Einsteinkoeffizienten besteht folgende Beziehung, wenn kein Zustand entartet ist:
Sind Zustände entartet, so ist zusätzlich das Gewicht gi der Entartung zu berücksichtigen:
Die Einsteinkoeffizienten sind temperaturunabhängig. Der Einsteinkoeffizient A21 ist eine Eigenschaft des Übergangs und stoffspezifisch. Die Temperaturabhängigkeit der Energieverteilung der Wärmestrahlung ist eine Folge der unterschiedlichen Besetzungswahrscheinlichkeiten N1 und N2 in Abhängigkeit von der Temperatur, die in der Regel durch die Boltzmann-Verteilung beschrieben wird. Siehe auch: Besetzungsinversion Literatur
|
| Dieser Artikel basiert auf dem Artikel Einsteinkoeffizienten aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




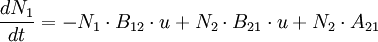
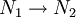 z. B. durch Wärmestrahlung.
z. B. durch Wärmestrahlung.
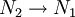 z. B. durch Wärmestrahlung.
z. B. durch Wärmestrahlung.
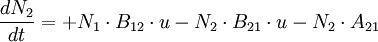
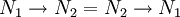 .
.
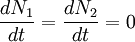 ist.
ist.