Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
BesetzungsinversionBesetzungsinversion ist ein Begriff aus der Physik, genauer der Quantenmechanik und beschreibt den Zustand eines Systems, in dem mehr Teilchen einen energetisch höheren Zustand N2 besetzen als den energetisch niedrigeren Zustand N1. Dies ist im thermischen Gleichgewicht nach der Boltzmann-Verteilung nicht möglich, wenn eine einheitliche Temperatur vorausgesetzt wird. Im thermischen Gleichgewicht gilt die Boltzmann-Gleichung:
Produkt-Highlight
gi: statistisches Gewicht des Zustandes i Eine Besetzungsinversion liegt vor, wenn Nach der Gleichung kann dem Zustand '2' eine höhere Temperatur als dem Zustand '1' zugeordnet werden. Da ein System danach strebt, seine Entropie zu maximieren, ist die Besetzungsinversion nicht stabil und muss durch Aufwenden von Energie, dem Pumpen, künstlich herbeigeführt und aufrechterhalten werden. Das Pumpen muss selektiv erfolgen, so dass nur ausgewählte Niveaus der Teilchen stärker besetzt werden. Die notwendige Energie kann durch optisches Pumpen eingebracht werden, wobei Blitzlampen oder die Strahlung anderer Laser genutzt werden kann. Die Energie des Photons ist proportional zur Frequenz oder Wellenlänge der Strahlung:
Eine Besetzungsinversion wird erreicht, wenn Photonenenergie der Pumpquelle und die Energiedifferenz zwischen dem Grund- und einem höher angeregten elektronischen Zustand des Teilchens übereinstimmen. Eine andere Form der selektiven Anregung ist der Stoß mit einem anderen angeregten Teilchen (B), das durch Abregung die Energiedifferenz austauschen kann, um das erste Teilchen (A) in den höher angeregten Zustand zu bringen. Um die Teilchen der Sorte B nach der Stoßabregung wieder in den angeregten Zustand zu bringen, muss ihnen Energie, z. B. durch Elektronenstöße, zugeführt werden (siehe He-Ne-Laser). Die Energie kann in Form einer elektrischen Entladung (z. B. Glimmentladung, Hohlkathode, Mikrowelle) in das Medium eingebracht werden.
Wird die Anregungsquelle (z. B. optisches Pumpen, Gasentladung) abgeschaltet, dann wird die thermische Überbesetzung des invertierten elektronischen Zustands durch Emission und Stöße mit anderen Atomen oder Molekülen abgebaut. Das lokale thermische Gleichgewicht wird erreicht, wenn angeregte elektronische Zustände, Ionisationsgrad und die kinetische Bewegungsenergie der Atome/Moleküle entsprechend der Boltzmann-Statistik verteilt sind. Voraussetzung ist eine hohe Teilchendichte, um eine hohe Stoßrate und somit Energieaustausch zu erzielen. LaserEin Laser stellt eine Anordnung dar, einen Lichtstrahl zu erzeugen, dessen Photonen sich durch gleiche Frequenz, Phase und Schwingungsrichtung (kohärente Strahlung) auszeichnen. Die nutzbare Strahlung wird dem Strahlungsfeld in einem Resonator ausgekoppelt. Die Voraussetzung für den Betrieb eines Lasers ist die Verstärkung eines Strahls durch stimulierte Emission. Dazu muss das Besetzungsverhältnis der beiden Zustände 1 und 2 invertiert sein. Dies kann stationär nur erreicht werden, wenn der untere Zustand 1 schnell relaxiert und die Lebensdauer kürzer ist als die durch spontane Emission bestimmte Lebensdauer des oberen Zustands. Der untere Zustand muss schnell entleert werden, damit die Besetzungsinversion erhalten bleibt. Dagegen muss der obere Zustand 2 langlebig sein, damit die Besetzung nicht durch spontane Emission soweit reduziert wird, dass keine ausreichende Rate der stimulierten Emission auftritt. Im detaillierten Gleichgewicht stehen die Strahlungsprozesse im Gleichgewicht:
spontane Emission + stimulierte Emission = Absorption A21: Einsteinkoeffizient für spontante Emission B12: Einsteinkoeffizient für Absorption B21: Einsteinkoeffizient für stimulierte Emission Die Einsteinkoeffizienten stellen Übergangswahrscheinlichkeiten dar. Der Koeffizient für stimulierte Emission steht mit dem für Absorption in Zusammenhang: B21=(g1/g2) B12. Das detaillierte Gleichgewicht gilt im Nichtgleichgewichtszustand nur mikroskopisch; die Strahlungsdichte nimmt über die Weglänge zu. In einem Laser wird Strahlung der Laserwellenlänge optisch verstärkt. Die Besetzungsinversion ist eine notwendige aber nicht hinreichende Voraussetzung für den Betrieb eines Lasers. |
| Dieser Artikel basiert auf dem Artikel Besetzungsinversion aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


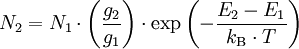 ,
,


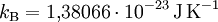 : Boltzmann-Konstante
: Boltzmann-Konstante
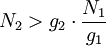 .
.
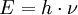 ,
,
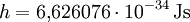 Planck-Konstante
Planck-Konstante
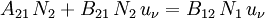 ,
,


