Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Ăberblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
ElastizitĂ€tsmodulDer ElastizitĂ€tsmodul (auch: Zugmodul oder Youngscher Modul, benannt nach dem englischen Arzt und Physiker Thomas Young) ist ein Materialkennwert aus der Werkstofftechnik, der den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear elastischem Verhalten beschreibt. Der ElastizitĂ€tsmodul wird mit E-Modul oder als Formelzeichen mit E abgekĂŒrzt. Der Plural von ElastizitĂ€tsmodul ist ElastizitĂ€tsmodule. Der ElastizitĂ€tsmodul hat die Einheit einer Spannung. Anschaulich formuliert ist der ElastizitĂ€tsmodul eines Materials diejenige Zugspannung, bei welcher sich ein Zugstab aus diesem Material in der LĂ€nge verdoppelt. (In der RealitĂ€t tritt dieser Fall nie auf, eine Verdoppelung der LĂ€nge (Dehnung um 100%) ist bei keinem Material eine linear-elastische Deformation.) Der Betrag des ElastizitĂ€tsmoduls ist um so gröĂer, je mehr Widerstand ein Material seiner Verformung entgegensetzt. Ein Bauteil aus einem Material mit hohem ElastizitĂ€tsmodul (z. B. Stahl) ist also steif, ein Bauteil aus einem Material mit niedrigem ElastizitĂ€tsmodul (z. B. Gummi) ist nachgiebig. Der ElastizitĂ€tsmodul ist die ProportionalitĂ€tskonstante im Hookeschen Gesetz. Bei kristallinen Materialien ist der ElastizitĂ€tsmodul grundsĂ€tzlich richtungsabhĂ€ngig. Sobald ein Werkstoff eine kristallographische Textur hat, ist der ElastizitĂ€tsmodul also anisotrop. Weiteres empfehlenswertes Fachwissen
DefinitionDer ElastizitĂ€tsmodul ist als Steigung des Graphen im Spannungs-Dehnungs-Diagramm bei einachsiger Belastung innerhalb des linearen ElastizitĂ€tsbereichs definiert. Dieser lineare Bereich wird auch als Hookesche Gerade bezeichnet. Dabei bezeichnet σ die mechanische Spannung (Normalspannung, nicht Schubspannung) und ε die Dehnung. Die Dehnung ist das VerhĂ€ltnis von LĂ€ngenĂ€nderung zur ursprĂŒnglichen LĂ€nge. Die Einheit des ElastizitĂ€tsmoduls ist die einer Spannung:
Der ElastizitĂ€tsmodul wird als Materialkonstante bezeichnet, da mit ihm und den Querkontraktionszahlen das ElastizitĂ€tsgesetz aufgestellt wird. Der ElastizitĂ€tsmodul ist aber nicht bezĂŒglich aller physikalischen GröĂen konstant. Er hĂ€ngt von verschiedenen Umgebungsbedingungen wie z. B. Temperatur, Feuchte oder der Verformungsgeschwindigkeit ab. AnwendungBei ideal linear elastischem Werkstoffgesetz (ProportionalitĂ€tsbereich im Spannungs-Dehnungs-Diagramm) ergibt sich die Federkonstante D eines geraden Stabes aus seiner QuerschnittsflĂ€che A, seiner LĂ€nge L0 und seinem ElastizitĂ€tsmodul E. Mit den AusdrĂŒcken und daraus den E-Modul Typische ZahlenwerteHinweise zur Einheitenumrechnung:
Kategorien: Werkstoffeigenschaft | Festigkeitslehre |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel ElastizitĂ€tsmodul aus der freien EnzyklopĂ€die Wikipedia und steht unter der GNU-Lizenz fĂŒr freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfĂŒgbar. | ||||||||||||||||||||||||||||||||||||||||||||||||||





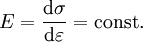
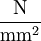 , in
, in 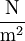 (
(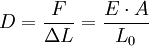
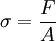 fĂŒr die Spannung und
fĂŒr die Spannung und 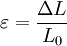 fĂŒr die Dehnung erhĂ€lt man aus obiger Gleichung das Hookesche Gesetz fĂŒr den 1-achsigen Spannungszustand
fĂŒr die Dehnung erhĂ€lt man aus obiger Gleichung das Hookesche Gesetz fĂŒr den 1-achsigen Spannungszustand
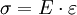
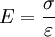
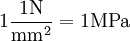 (Ein Newton pro Quadratmillimeter ist ein Mega-Pascal)
(Ein Newton pro Quadratmillimeter ist ein Mega-Pascal)
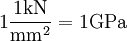 (Ein Kilo-Newton pro Quadratmillimeter ist ein Giga-Pascal)
(Ein Kilo-Newton pro Quadratmillimeter ist ein Giga-Pascal)
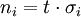 . Daher setzt man hier einen dickenbezogenen ElastizitĂ€tsmodul ein, was einer Steifigkeit entspricht. Diese GröĂe hat die Einheit
. Daher setzt man hier einen dickenbezogenen ElastizitĂ€tsmodul ein, was einer Steifigkeit entspricht. Diese GröĂe hat die Einheit 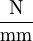 .
.
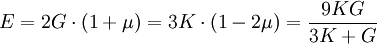
![\varepsilon_x = \frac 1 E \cdot [\sigma_x - \mu \cdot ( \sigma_y + \sigma_z)]](images/math/b/2/9/b2945e22e38223923095308709d1601b.png) .
.


