Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Magnetischer Fluss
Der Magnetische Fluss (Formelzeichen: Φ) ist in einem magnetischen Feld H ein Verhältnis zwischen der magnetischen Spannung Um und dem als Raumeigenschaft bzw. Materialeigenschaft im betrachteten Flussbereich vorhandenen magnetischen Widerstand Rm: Produkt-HighlightHerrscht beispielsweise im einfachsten linearen, homogenen Fall zwischen den mit den Abstand d zueinander befindlichen Polschuhen eines Magneten die magnetische Feldstärke H, so herrscht entlang der Strecke d die magnetische Spannung: Durch diese magnetische Spannung bildet sich zwischen den Polschuhen der magnetische Fluss aus. Je nach dem magnetischen Widerstand des zwischen den Polschuhen befindlichen Materials (bzw. des leeres Raumes) stellt sich eine bestimmte Größe des magnetischen Flusses ein. Der magnetische Widerstand ist dabei an die magnetische Leitfähigkeit als Stoff- bzw. Naturkonstante gebunden, so wie ein ohmscher Widerstand an die Stoffkonstante der elektrischen Leitfähigkeit des Widerstandsmaterials gebunden ist. Im Regelfall arbeitet man in der Feldtheorie nicht direkt mit dem magnetischen Fluss sondern mit der damit verknüpften magnetischen Flussdichte. Der Grund liegt darin, dass man einen Fluss nur einer bestimmten Fläche im Raum zuordnen kann, nicht aber diskreten Feldpunkten - es existiert keine Funktion Φ(x,y,z) wenn x,y,z Ortskoordinaten bezeichnen. Zeichnerisch wird daher der magnetische Fluss als eine Art "Röhre" (Flussröhre) dargestellt. Um diese Schwierigkeiten zu vermeiden, wird daher meist mit der vektoriellen Größe der magnetischen Flussdichte gearbeitet. Umgekehrt lässt sich so der magnetische Fluss durch eine Fläche A aus der magnetischen Flussdichte B ableiten als: Besondere Fälle
Daher ist der magnetische Fluss durch eine geschlossene Oberfläche eines Raumsegmentes immer Null, da nach dem Integralsatz von Gauß gilt: MaßeinheitDie Maßeinheit des magnetischen Flusses im SI-Einheitensystem ist Weber, das Einheitenzeichen Wb: QuantentheorieBei der Betrachtung von Quantenphänomenen (z. B. Aharonov-Bohm-Effekt, Quanten-Hall-Effekt) ist das magnetische Flussquantum Φ0 = h / (2e) (Quotient aus dem planckschem Wirkungsquantum und der Elementarladung) eine zweckmäßige Einheit. |
||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Magnetischer_Fluss aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. | ||||||||||||||||||||


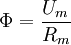



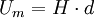
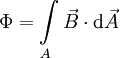
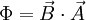
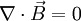
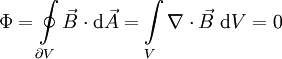
![[\Phi]=\mathrm{T \cdot m^2} = \mathrm{Vs} = \mathrm{Wb}](images/math/1/b/b/1bbd58e9c8667c62dfc52fcd175effbc.png)


