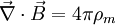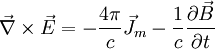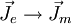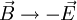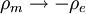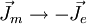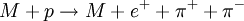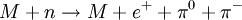Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Magnetischer MonopolUnter magnetischen Monopolen (die Betonung liegt auf der ersten Silbe, entsprechend Dipol, nicht wie beim Wirtschaftsmonopol) versteht man in der Physik hypothetische Teilchen, die eine magnetische Ladung tragen, also nur entweder einen magnetischen Nord- oder Südpol darstellen. Sie wären somit, analog zu elektrischen Ladungen, Quellen beziehungsweise Senken des magnetischen Feldes. Jedoch kennt man in der beobachteten Natur bisher nur magnetische Wirbelfelder, die entweder durch atomare magnetische Momente (Permanentmagnete) oder in Spulen durch bewegte elektrische Ladungen (Ströme) erzeugt werden und keine Quellen und Senken besitzen. Produkt-Highlight
Theoretische HinweiseIn der Vergangenheit wurden in unterschiedlichen Bereichen der theoretischen Physik Überlegungen über magnetische Monopole angestellt. Von Paul A. M. Dirac stammt die Spekulation, es könne einen magnetischen Monopol (d. h. „Einzelpol“) als Elementarteilchen geben, welches das magnetische Gegenstück zum Elektron wäre. Damit wäre eine merkwürdige Asymmetrie zwischen den sonst einander so ähnlichen Erscheinungen Magnetismus und Elektrizität behoben. Außerdem ließe sich dann leicht erklären, warum die elektrische Ladung stets nur in ganzzahligen Vielfachen der Elementarladung auftritt. Beide Argumente werden in den folgenden Abschnitten erläutert. Trotz intensiver Bemühungen konnte bisher allerdings die Existenz eines solchen Teilchens nicht nachgewiesen werden (siehe unten). Maxwell-Gleichungen und SymmetrieSymmetrien spielen in der Physik eine fundamentale Rolle. Die im 19. Jahrhundert formulierten Maxwell-Gleichungen, die die elektrischen und magnetischen Phänomene beschreiben, lassen eine unnatürlich wirkende Asymmetrie zwischen der elektrischen Feldstärke E und der magnetischen Flussdichte B erkennen. Während die elektrischen Ladungen als Ladungsdichte ρe und zugehörige Stromdichte
Nimmt man jedoch die Existenz von magnetischen Ladungen (Monopolen) an, gibt es auch eine von Null verschiedene magnetische Ladungsdichte ρm und magnetische Stromdichte
Man erhält nun also eine Theorie, die unter folgenden Transformationen unverändert bleibt:
Die Existenz magnetischer Monopole würde also die Unterschiede zwischen elektrischem und magnetischem Feld weiter verringern und wäre von diesem Standpunkt aus gesehen "wünschenswert", da es ohnehin möglich ist, durch einen Wechsel des Bezugssystems mittels Lorentz-Transformation E- und B-Felder (teilweise) ineinander zu überführen. Die Quantisierung der elektrischen LadungAußer dem Drehimpuls ist auch die elektrische Ladung quantisiert, d.h., sie tritt nur als ganzzahliges Vielfaches der Elementarladung auf. Nach Dirac würde das Vorhandensein magnetischer Monopole diesen Umstand leicht erklären: Ein sich im Feld eines Monopols bewegendes Elektron wird auf eine Kreisbahn abgelenkt. Die Quantenmechanik fordert die Quantisierung des Drehimpulses; die mit der Ablenkung einhergehende Änderung des Drehimpulses, die proportional zur elektrischen Ladung ist, kann also nur in bestimmten diskreten Schritten erfolgen. Daher folgt aus der Existenz des magnetischen Monopols direkt die Quantisierung der elektrischen Ladung. Die Überlegung würde in gleicher Weise auch für die magnetische Ladung gelten. Der Monopol wäre also Träger der magnetischen Elementarladung. Magnetische Monopole als SolitonenEin Hinweis auf die Existenz magnetischer Monopole ergibt sich aus den sogenannten Theorien der großen Vereinheitlichung (GUT). Diese Theorien beschreiben die Vereinheitlichung der Elektroschwachen Kraft mit der Starken Kraft bei hohen Energien, wie sie bis etwa 10-36 Sekunden nach dem Urknall in unserem Universum herrschten. Durch die Abkühlung des expandierenden Universums sank die typische Teilchenenergie zu diesem Zeitpunkt unter einen kritischen Wert von ungefähr 1015 GeV. Dadurch wurde die Symmetriebrechung der vereinheitlichten Kraft in die separaten Kräfte Starke Wechselwirkung und Elektroschwache Wechselwirkung ausgelöst. Dabei traten unter anderem stabile punktförmige topologische Defekte des Eichfeldes, sogenannte Solitonen, auf - die magnetischen Monopole. Dieser Mechanismus ist in etwa mit den Vorgängen in erstarrenden Flüssigkeiten zu vergleichen. Die Kristallisation startet gleichzeitig an verschiedenen Raumpunkten. Wachsen nun zwei Kristalle zusammen, entstehen an den Kontaktflächen Gitterdefekte. Die Dichte der entstandenen Monopole lässt sich zum Zeitpunkt der Entstehung auf etwa 1082 m-3 abschätzen. Die Tatsache, dass die Teilchendichte heutzutage signifikant niedriger liegt, wird auch als ein weiterer Hinweis auf eine starke inflationäre Phase des frühen Universums gesehen. Eigenschaften der MonopoleDie gegenwärtigen Theorien zeichnen ein konkretes Bild vom Aufbau und den Eigenschaften eines GUT-Monopols. Er besitzt eine Masse von etwa 1016 GeV und einen Durchmesser von ungefähr 10-15 m. Darüber hinaus verfügt er über weitere erwähnenswerte Eigenschaften: Substruktur magnetischer MonopoleMagnetische Monopole besitzen eine zwiebelähnliche Unterstruktur. In der Nähe des Zentrums, d.h. im Bereich von 10-31 m liegt ein GUT-symmetrisches Vakuum vor. Daran schließt sich eine Schale der sogenannten elektro-schwachen Vereinigung an mit Teilchen wie den Eichbosonen der schwachen Wechselwirkung W+, W- und Z0. Diese Zone geht bei etwa 10-18 m in die Confinement-Schale über, die mit Gluonen und Photonen angefüllt ist. Die äußerste Schale wird aus Fermion-Antifermion-Paaren gebildet. Verletzung der ZeitumkehrinvarianzUntersucht man die Ablenkung eines geladenen Teilchens in der Umgebung eines Monopols, so stellt man fest, dass eine solche Anordnung die Zeitumkehrinvarianz verletzt. Das bedeutet, der Prozess verläuft bei Umkehrung der Zeitrichtung nicht in der selben Art und Weise ab. Diese Tatsache sprach lange Zeit direkt gegen die Existenz von magnetischen Monopolen. Nachdem jedoch im Jahre 1964 die CP-Verletzung im Zerfall der K-Mesonen nachgewiesen werden konnte, folgt aus dem CPT-Theorem direkt die Existenz T-invarianzverletzender Prozesse. Katalyse des ProtonenzerfallsAufgrund der oben genannten inneren Struktur können GUT-Monopole den Protonen- und Neutronenzerfall katalysieren. Dabei werden folgende Reaktionen von den Theorien vorhergesagt (M steht für den Monopol):
Der Monopol selbst zerfällt bei diesen Reaktionen nicht. Durch diese Zerfallsprozesse ist er also in der Lage, die Stabilität von Materie zu beeinflussen. Experimentelle SucheDa der magnetische Monopol eine sehr hohe Ruheenergie besitzt – seine Masse ist mit der eines Bakteriums vergleichbar – ist es nicht möglich, ihn in Colliderexperimenten direkt zu erzeugen und nachzuweisen. Deshalb ist man bei der Suche nach Monopolen auf deren natürlich vorhandene Flussdichte angewiesen, die jedoch von den gängigen Theorien als sehr niedrig vorhergesagt wird. Aufbau typischer NachweisexperimenteEin mögliches Experiment zum Nachweis des hypothetischen Teilchens basiert auf der Verwendung supraleitender Spulen. Beim Durchgang eines Monopols durch eine solche Spule wird durch die Änderung des magnetischen Flusses ein Ringstrom induziert, der nachgewiesen werden kann. Ein solcher Kreisstrom ist tatsächlich nur mittels magnetischer Monopole und nicht etwa durch das Feld eines herkömmlichen Dipolmagneten erzeugbar. Jedoch erfordert die relativ große Störanfälligkeit solcher Experimente eine sorgfältige Versuchsdurchführung. Weitere Experimente, wie beispielsweise Superkamiokande (das Kamiokande-Nachfolgeexperiment), zielen auf den Nachweis des oben beschriebenen durch Monopole induzierten Protonenzerfalls. Hierbei dienen als Protonenträger beispielsweise mehrere tausend Tonnen hochreines Wasser. Die Abschätzung der zu erwartenden Zerfallsrate setzt allerdings die Kenntnis des typischen Wirkungsquerschnitts der Zerfallsreaktion voraus. ErgebnisseAlle bisher zum Nachweis magnetischer Monopole durchgeführten Experimente waren erfolglos. Lediglich ein einziges Ereignis konnte im Februar 1982 von Blas Cabrera (Stanford University, USA) in einem Spulenexperiment beobachtet werden. Es kann jedoch nicht ausgeschlossen werden, dass es sich hierbei um eine Fehlsignatur handelt. Gegenwärtige Experimente geben deshalb stets Obergrenzen des Teilchenflusses an, die derzeit, abhängig von der verwendeten Methode, etwa im Bereich von 10-16 s-1cm-2sr-1 liegen. Das bedeutet umgerechnet, dass eine Fläche von 1 m2 im Durchschnitt höchstens alle 30.000 Jahre von einem Monopol durchquert wird. Kategorien: Magnetismus | Elektrodynamik |
|||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Magnetischer_Monopol aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





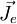 auftreten, sind wegen der Nichtexistenz magnetischer Ladungen die entsprechenden magnetischen Größen gleich Null:
auftreten, sind wegen der Nichtexistenz magnetischer Ladungen die entsprechenden magnetischen Größen gleich Null:
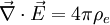
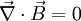
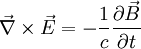
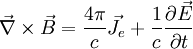
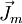 , so dass die Gleichungen dann lauten:
, so dass die Gleichungen dann lauten: