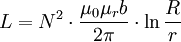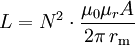Toroidspule

Eine Toroidspule, auch Kreisringspule, Ringspule oder Ringkernspule genannt, ist in der Elektrotechnik eine speziell geformte Spule, die aus einem Kern in Form eines Kreisringes besteht (sogenannter Ringkern), um den herum der elektrische Leiter gewickelt wird. Die Besonderheit dieser Bauform liegt darin, dass sich der magnetische Fluss fast ausschließlich im kreisförmigen Kern ausbreitet und das meist störende Streufeld im Außenraum der Kreisringspule vergleichsweise schwach ist.

Weiteres empfehlenswertes Fachwissen

Tägliche Sichtkontrolle der Laborwaagen

Wie kann man Pipetten schnell überprüfen?

Was ist der richtige Weg, um die Wiederholbarkeit bei Waagen zu überprüfen?

Ausführungsformen und Anwendungen

  Kreisringspulen werden vor allem in passiven elektrischen Filtern zur Unterdrückung unerwünschter hochfrequenter Störungen eingesetzt. Die Ausführung kann dabei als klassische Spule mit nur einem Leiter erfolgen; aber auch zwei oder mehr Leiter auf dem Spulenkörper sind möglich. Um eine magnetische Sättigung des Kerns zu vermeiden, sind entweder entsprechende Werkstoffe als Kernmaterial notwendig oder es wird in den Kreisring künstlich ein Luftspalt eingebaut.

Bei zwei Wicklungen, wie in der nebenstehenden Abbildung zu sehen, spricht man auch von einer stromkompensierten Drossel, bei der kein Luftspalt notwendig ist: Bei dieser Bauform fließen die Ströme durch beide Leiter in entgegengesetzter Richtung, und deren magnetische Flüsse heben sich im Kern auf. Bei Störsignalen, welche in gleicher Richtung über beide Leiter fließen, kommt es hingegen zu keiner gegenseitigen Auslöschung des magnetischen Flusses, und es erfolgt durch die Induktivität eine starke Drosselung der Störungen.

Toroidspulen mit zwei oder mehr Wicklungen werden als wesentliches Bauelement auch in Fehlerstromschutzschaltern zur Erkennung eines Fehlerstromes eingesetzt.

Ein besonderer Einsatzbereich ist die Verwendung als Transformator. Dabei wird die Spannung von einer Wicklung, der Primärseite, auf die zweite Wicklung, die Sekundärseite, übertragen. In dieser Anwendung darf der Kern keinen Luftspalt aufweisen, und das Bauteil wird dann als Ringkerntransformator bezeichnet.

Berechnung der Induktivität

Die Induktivität L einer Toroidspule mit einer Wicklung mit N Windungen und einem rechteckförmigen Kern der Breite b, dem Innenradius r und dem Außenradius R lässt sich näherungsweise bei dünnem Draht mit der Formel

berechnen. Dabei ist μ₀ist die magnetische Feldkonstante und μ_r die Permeabilitätszahl des Kernmaterials. Statt der Radien können auch die entsprechenden Durchmesser eingesetzt werden.

Wenn der relative Unterschied zwischen äußerem und innerem Radius des Ringes gering ist, der mittlere Radius mit r_m = (R + r) / 2 und die Querschnittsfläche des Ringes mit A bezeichnet wird, so kann man die Induktivität der Ringspule näherungsweise zu

berechnen.^[1][2][3]

Siehe auch

• Zylinderspule

Quellen

1. ↑ Karl Küpfmüller: Einführung in die theoretische Elektrotechnik. 13. Auflage, 1990, Springer-Verlag.
2. ↑ N. Fliege, Universität Mannheim: Vorlesung Elektrotechnik I, Kapitel 2: Elektrische Bauelemente und Netzwerke (PDF, 1,5 MB).
3. ↑ P. Weiß, Universität Kaiserslautern: Skript zur Vorlesung Grundlagen der Elektrotechnik (PDF, 4,9 MB).