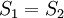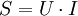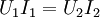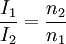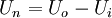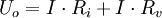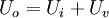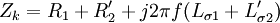Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
TransformatorEin Transformator (kurz: Trafo) ist ein elektrotechnisches Betriebsmittel, das vor allem dazu dient, elektrische Energie auf ein anderes elektrisches Spannungsniveau zu übertragen. Das Verhältnis der Stromstärken an Ein- und Ausgangsklemmen ist dabei umgekehrt zu dem Verhältnis der dort gemessenen Spannungshöhen (wenn man die Verluste vernachlässigt). Die Höhe der Wechselspannung, mit der die elektrische Energie übertragen wird, kann mit Hilfe von Transformatoren sowohl erhöht als auch verringert und damit den Erfordernissen angepasst werden. Damit wird die wirtschaftliche Übertragung elektrischer Energie über weite Strecken mit Hochspannungsleitungen möglich. Die "hineingesteckte" Leistung wird von einem Trafo jedoch nicht vergrößert, da in ihm immer Verluste auftreten. Ein Transformator besteht mindestens aus einer Spule mit mehreren Anzapfungen oder aus zwei oder mehreren getrennten Spulen, die induktiv, also magnetisch gekoppelt sind. Zur optimalen Führung des magnetischen Flusses im so genannten Transformatorkern und um die magnetische Kopplung der Spulen untereinander zu maximieren, haben praktische Ausführungen von Transformatoren ihre Spulen meist auf einem gemeinsamen Eisen- oder Ferritkern untergebracht. In der Terminologie elektrotechnischer Geräte wird der Transformator auch als „ruhende elektrische Maschine“ bezeichnet, da dabei keine mechanisch bewegten Teile vorhanden sind. Transformatoren zur Leistungsübertragung nennt man Umspanner, Transformatoren für messtechnische Zwecke werden als Messwandler bezeichnet, und Transformatoren zur Signalübertragung in der Nachrichtentechnik, wo es um die galvanische Trennung von Ein- und Ausgangssignal geht, werden als Übertrager bezeichnet.
Produkt-HighlightGeschichtliche AnfängeDie Erscheinung der Magnetfelderzeugung aus dem elektrischen Stromfluss und umgekehrt der Stromerzeugung aus einem veränderlichen Magnetfeld war seit Michael Faradays Entdeckungen 1831 bekannt. Aber erst in den achtziger Jahren des selben Jahrhunderts wurde das Transformator-Prinzip entwickelt. Der russische Erfinder Pawel Nikolajewitsch Jablotschkow führte für die von ihm entwickelten Jablotschkow’sche Kerzen eine Spannungsregulierung ein, die auf einer Anordnung von Induktionsspulen basierte. Die Windungen der einen Spule waren mit einer Wechselstromquelle verbunden, die anderen mit den Kohle-Elektroden der elektrischen Kerzen. Das dafür eingereichte Patent beschrieb, dass das System „unterschiedliche Versorgungen für verschiedene Beleuchtungskörper mit unterschiedlicher Leuchtintensität von einer einzigen Quelle elektrischer Energie“ versorgen könne [1]. Offensichtlich wirkten diese Induktionsspulen nach dem Transformator-Prinzip. Lucien Gaulard und John Dixon Gibbs stellten in London 1882 ein Gerät mit einem offenen Eisenkern aus, das sie “Sekundär-Generator” nannten [2]. Sie betrieben mit ihrem System auf der Ausstellung in Turin 1884 eine 80 km lange Demonstrations-Ringleitung nach Lanzo und führten damit die verlustarme Stromversorgung über größere Entfernungen vor. Sie verkauften zudem die Idee an den Amerikaner George Westinghouse. Die in der ungarischen Industriefirma Ganz & Cie tätigen Techniker Károly Zipernowsky und Miksa Déri entwarfen 1884 den zweiteiligen rotierenden Einankerumformer. Zusammen mit Ottó Titusz Bláthy entwickelten sie diese Apparatur zu einem feststehenden einteiligen Gerät weiter und ließen sich dies 1885 patentieren. Erstmals wurde dabei der Begriff "Transformator" verwendet. [3]. Dieser Transformator war mechanisch nach dem umgekehrten Prinzip der heutigen Transformatoren aufgebaut; die Leiterspulen waren um einen soliden Kern aus unmagnetischem Material gewunden, darüber wurden dicke Eisendraht-Lagen gelegt, die eine ferromagnetische Schale bildeten. Das Gerät wurde von der Firma Ganz & Cie in Budapest weltweit vertrieben. Wesentlichen Anteil an der Verbreitung des Wechselstromsystems und mit ihm des Transformators hatte der US-Amerikaner George Westinghouse, der vor allem durch die Erfindung der Druckluftbremse berühmt wurde. Westinghouse erkannte die Schwächen der damals von Edison betriebenen und favorisierten Gleichstrom-Energieverteilung und setzte vorrangig auf Wechselstrom. 1885 importierte Westinghouse eine Anzahl Gaulard-Gibbs-Transformatoren und einen Siemens-Wechselspannungsgenerator für die elektrische Beleuchtung in Pittsburgh. Sein Techniker William Stanley entwickelte die Gaulard-Gibbs Geräte weiter und führte vor allem einen effektiver wirkenden geschlossenen Eisenkern ein. Ab 1886 gelangten diese Apparate in den Handel [4]. Westinghouse installierte 1886 in Great Barrington, Massachusetts, einen Wechselspannungsgenerator, dessen 500 Volt Wechselspannung zur Verteilung auf 3.000 Volt hochtransformiert und dann zum Betrieb der elektrischen Beleuchtung an den Anschlussstellen wieder auf 100 Volt heruntertransformiert wurde. Der dann zunehmende Einsatz von Transformatoren führte in Verbindung mit dem Wechselstrom zur weiten Verbreitung von Elektrizität als Energielieferanten, weil nur Hochspannungsleitungen den Energietransport über große Entfernungen ohne allzu große Energieverluste ermöglichen. Physikalische GrundlagenFür die Wirkweise eines Transformators sind zwei physikalische Erscheinungen wesentlich:
Eine an die erste Spule („Primärspule“) im Primärstromkreis angelegte Wechselspannung erzeugt dem Induktionsgesetz folgend ein veränderliches Magnetfeld im Kern. Dieses Feld durchsetzt die zweite Spule („Sekundärspule“) in einem zweiten Stromkreis und erzeugt hier durch Induktion wiederum eine Spannung („Sekundärspannung“). Eine primäre Spannung kann über magnetischen Fluss in eine proportionale sekundäre Spannung als Funktion von dem Windungszahlverhältnis der beiden Spulen transformiert werden. Zum Betrieb eines Transformators ist eine in stetem Wechsel veränderliche Spannung nötig. Daher kann mit einem Transformator nur Wechselspannung transformiert werden. Soll eine Gleichspannung mittels Transformatoren auf eine andere Spannungsebene umgesetzt werden, ist die Umwandlung des Gleichstroms in Wechselstrom mittels Wechselrichter nötig, um anschließend transformiert werden zu können. Diese Techniken finden beispielsweise bei Schaltnetzteilen Anwendung. Die maximale Höhe der induzierten Spannung hängt neben der Eingangsspannung von der Windungszahl der Sekundärspule ab, die maximale Höhe des Stromes von deren Leiterquerschnitten und von den Kühlungsbedingungen. In obiger Beschreibung wird kein (gemeinsamer) Eisenkern der Spulen erwähnt, trotzdem besitzen fast alle Transformatoren einen Kern aus Eisenblechen, Eisendrähten oder Ferrit. Der Grund liegt darin, dass bei tiefen Frequenzen (50 Hz) ohne Eisenkern extrem viele Windungen erforderlich wären, um den „Leerlaufstrom“ bei geringer Belastung ausreichend klein zu halten. Das würde erstens einen unwirtschaftlich hohen Kupferanteil erfordern, andererseits werden bei höheren Strömen in diesem sehr langen Draht enorme Ohmsche Verluste (=Erwärmung) erzeugt. Beides kann man stark verringern, indem die Induktivität der Primärspule durch einen Eisenkern um ein Vielfaches vergrößert wird. Je höher die Betriebsfrequenz ist, desto kleiner kann der Eisenkern sein, bei einigen 100 kHz wie im Tesla-Transformator darf er vollständig entfallen. Praktische AusführungSchutztransformatorenSie sollen eine Anlage oder Geräte zum Schutz gegen Berührung spannungsführender Teile mit einer Sekundärspannung versorgen, die galvanisch von der Spannung auf der Primärseite getrennt ist. Eine sichere galvanische Trennung von Primär- und Sekundärspannung muss gewährleistet sein. Die Schutzwirkung besteht darin, dass auf der Sekundärseite jeder der beiden Pole für sich ohne Stromschlag berührt werden kann. (siehe auch: Sicherheitstransformator) TrenntransformatorenDie Nennspannung auf der Sekundärseite des Trenntransformators darf nicht höher sein als 400 V, die Kurzschluss-Spannung darf den Wert 10 % nicht überschreiten. Es handelt sich um Einphasen-Transformatoren, bei denen eine vollkommene galvanische Trennung der Primär- und Sekundärwicklung vorhanden ist. KlingeltransformatorenKlingeltransformatoren müssen kurzschlussfest sein (Uk = 40 %), die Leerlaufspannung auf der Sekundärseite darf 32 V nicht übersteigen. Die Ausgangsklemmen müssen zugänglich sein, ohne dass die Eingangsklemmen freigelegt werden müssen. SpielzeugtransformatorenSpielzeugtransformatoren haben meistens eine Kurzschluss-Spannung von 20 %. Sie dienen der Speisung von Kinderspielzeug, müssen kurzschlussfest sein und dürfen auf der Sekundärseite höchstens eine Leerlaufspannung von 32 V aufweisen (Nennspannung bei Belastung der Sekundärseite: 24 V). Die Spezifikation eines Spielzeugtransformators ist im Wesentlichen davon bestimmt, dass Kinderspielzeug in den Mund genommen wird. Anordnung als SpulenDie Ausführung eines Transformators aus ausgestreckt nebeneinanderliegenden Leitern würde bewirken, dass ein großer Teil des Magnetfeldes als wirkungsloses Streufeld in der Umgebung entsteht. Dieses Streufeld enthält einen großen Teil der aufgewendeten Leistung, die dann nicht für den eigentlichen Übertragungsvorgang zur Verfügung steht. Daher werden die Leiter in Form von Spulen angelegt. Um den Verlust durch Streufelder möglichst klein zu halten, werden auch die Primärspulen und Sekundärspulen möglichst klein und eng ineinandergeschachtelt. Eine Nebenbedingung ist hierbei, dass die Leiter und auch die Spulen als Ganzes gegeneinander elektrisch isoliert sind, wozu meistens lackierte Drähte und die nachfolgende Lack- oder Gießharztränkung im Vakuum angewendet werden. Der Spulenkörper ist ein aus nichtmagnetischem Material, meistens aus Kunststoff bestehendes Formteil, das die Wicklungen aufnimmt, ihnen mechanische Stabilität gibt und sie nötigenfalls auch voneinander isoliert. Die Spule, die vom Eingangsstrom gespeist wird, wird „Primärspule“ genannt, die Spule, in der die Spannung induziert wird, wird „Sekundärspule“ genannt. Das Verhältnis der Spannungen an den beiden Spulen entspricht in der Theorie exakt dem Verhältnis ihrer Windungszahlen (in der Praxis ist die Spannung an der Sekundärspule wegen Verlusten kleiner als in der Theorie). Beispiel: Ein Transformator mit 1.000 Windungen auf der Primärwicklung, 100 Windungen auf der Sekundärwicklung und 230 Volt Primärspannung erzeugt in der Sekundärwicklung eine Leerlaufspannung von 23 Volt. Diese Spannungen entstehen im Leerlauf-Betrieb des Transformators. Die tatsächlich nutzbare Betriebs- oder Nennspannung sinkt jedoch mit zunehmender Belastung durch Stromverbraucher, weil der Strom in den Spulen einen ohmschen Spannungsabfall bewirkt (siehe Abschnitt 4.5 Überlastbetrieb!). Lufttransformator bzw. eisenloser TransformatorDie kernlose Ausführung wird „Lufttransformator“ genannt und ist bei niedrigen Frequenzen nicht effizient. Ursache ist, dass die Primärspule dann extrem viele Windungen besitzen müsste, um den erforderlichen hohen induktiven Widerstand zu erzeugen. Der dann erforderliche sehr lange Draht hätte aber so großen Widerstand, dass darin ein Großteil der zugeführten Leistung in Wärme verwandelt würde. Lufttransformatoren haben den Vorteil, in der Sekundärspule eine Spannung mit exakter Nachbildung der zeitlichen Veränderung des Primärstroms zu liefern, auch wenn der Primärwechselstrom relativ hohe Frequenzen enthält. Diese Erscheinung kommt besonders dann zum Tragen, wenn die Frequenzanteile des Stromes sich über eine große Bandbreite erstrecken. Daher werden für manche Zwecke Lufttransformatoren als Übertrager verwendet. Weitere Beispiele sind der Teslatransformator sowie Koppel- und Anpassspulen in der Hochfrequenztechnik. EisenkerntransformatorDas von einem stromdurchflossenen Leiter erzeugte Magnetfeld ist in Luft oder im Vakuum mit einer Flussdichte von relativ geringer Stärke verbunden, magnetische Kopplung und Induktivität der Spulen sind gering und würden sehr hohe Betriebsfrequenzen erfordern. Es ist jedoch möglich, die Flussdichte erheblich zu steigern, indem das magnetische Feld der Spulen in einem geschlossenen magnetischen Kreis aus ferromagnetischem Material, z. B. Eisen – dem Trafokern – geführt wird. Für Netztransformatoren (Frequenzen von 50 oder 60 Hz) verwendet man überwiegend Eisen-Silizium-Legierungen, kornorientertes Elektroblech (Texturblech) nach DIN EN 10107. Bei Signalübertragern werden auch die höherwertigen Eisen-Nickel-Legierungen und bei hohen Frequenzen weichmagnetische Ferritkerne eingesetzt. Die Steigerung der Flussdichte bei ferromagnetischen Werkstoffen beruht darauf, dass sich mit zunehmender Stärke eines von außen angelegten Magnetfeldes die regellos ausgerichteten magnetischen Kristallbereiche (Weiss-Bezirke) in eine gemeinsame Richtung umordnen. Diese magnetische Polarisation M des Werkstoffes liefert einen 1.000 bis 100.000 mal höheren Beitrag zur Flussdichte B als die magnetische Feldstärke H. Diese Verhältniszahl nennt man Magnetische Suszeptibilität χ, es gilt Für die magnetische Flussdichte B gilt und daraus schließlich
Die dimensionslose Zahl μr = 1 + χ wird Relative Permeabilitätskonstante oder Permeabilitätszahl genannt und ist werkstoffspezifisch. Für die Leistungsübertragung im Stromnetz verwendete Transformatoren haben immer einen geschlossenen Eisenkern, auf den die Spulen aufgebracht werden. Der Querschnitt des Eisenkerns wird so gewählt, dass die Flussdichte möglichst im gesamten Eisen-Kern konstant ist und nicht zu nahe an die magnetische Sättigungsflussdichte kommt. Kerne für einphasige Transformatoren aus drei Schenkeln mit Primär- und Sekundärspule auf dem Mittelschenkel (M-Kerne) haben daher Außenschenkel mit dem halben Querschnitt des Mittelschenkels. Typische Flussdichten liegen bei kornorientiertem Elektroblech (2,03 Tesla Sättigungsflussdichte) bei 1,6…1,75 T. An manche Transformatoren werden besonders hohe Anforderungen an die Linearität der Strom-Spannungs-Kennlinie gestellt oder sie dienen gleichzeitig der Zwischenspeicherung magnetischer Energie (Sperrwandler). Dies kann durch einen Luftspalt im magnetischen Kreis erreicht werden (quasi eine Mischform von Lufttransformator und Eisenkerntransformator). Der Feldstärkebedarf und damit der Magnetisierungsstrom steigen, die Kennlinie wird geschert bzw. linearisiert. Die im Luftspalt gespeicherte magnetische Energie vergrößert die Blindleistung, wird jedoch fast verlustfrei wieder abgegeben. Leistungstransformatoren für Frequenzen unterhalb von etwa 1 kHz haben meistens Kerne, die aus elektrisch gegeneinander isolierten Eisenblechen (Elektroblech) bestehen. Die Kerne müssen geblecht sein, weil unter dem Einfluss des Magnetfeldes im Eisen als leitendem Material genauso wie in der Sekundärspule Spannungen induziert werden, die im Vollmaterial zu Wirbelströmen führen. Diese Wirbelströme erzeugen Verluste, die umso höher sind, je besser die elektrische Leitfähigkeit des Kernes ist. Der Stromweg wird durch die Verwendung von dünnen Blechen, die voneinander isoliert sind, unterbrochen. Eine Beschädigung der Isolierung der einzelnen Blechpakete kann bei großen Transformatoren zu einer erheblichen lokalen Erwärmung des Paketes führen. Der Eisenkern verursacht weiterhin Ummagnetisierungsverluste, die durch die fortwährende Umpolung der magnetischen Domänen (Weiss-Bezirke) entstehen und auch bei Leerlauf auftreten. Silizium-Eisen-Legierungen mit spezieller Textur haben bei Blechdicken von etwa 0,2 bis 0,3 mm bei 50 Hz Verluste von etwa 0,5 bis 1 W/kg je nach der Stärke des Magnetfelds, das durch die Spulen induziert wird. Das Magnetisierungsverhalten des Eisens ist bis zur Sättigungsflussdichte weitgehend linear. Durch das lineare Verhalten bleibt der aufgenommene Leerlauf-Wechselstrom weitgehend sinusförmig. Bei der Transformation bleibt die Kurvenform der Eingangsspannung weitestgehend erhalten – lediglich Oberwellen werden aufgrund der Streuinduktivität gedämpft, was jedoch bei Netztransformatoren sogar erwünscht ist. Ob ein Transformatorkern in die unerwünschte magnetische Sättigung gerät, hängt von der Höhe der Primärspannung ab – ist die Primärspannung in Bezug zu Kernquerschnitt bzw. Kernmaterial, Windungszahl und Frequenz zu hoch, gerät der Transformator in die Sättigung. Die Stromaufnahme steigt steil an. Die magnetische Sättigung setzt bei Belastung des Transformators bei etwas höherer Spannung ein, da die magnetische Feldstärke aufgrund des Spannungsabfalles am ohmschen Widerstand der Primärwicklung etwas abnimmt. Eine starke Belastung oder gar ein Kurzschluss der Sekundärseite führt zu einer wesentlich geringeren magnetischen Feldstärke im Kern und gleichzeitig zu einem starken Streufeld. Dieses kann zum Auslösen eines Kurzschlussschutzes (magnetische Sicherung) genutzt werden. Die Hysterese-Kennlinie bildet den Zusammenhang zwischen Magnetfeldstärke und Erregerfeld bei dessen Anstieg und Rückgang ab. An ihr kann man sowohl die Sättigungsinduktion als auch die Ummagnetisierungsverluste erkennen. Für Transformatoren für höhere Frequenzen werden für die Kerne statt Eisen auch andere weichmagnetische Werkstoffe wie z. B. Ferrite, amorphe Metallbandkerne oder Pulverkerne verwendet. RingkerntransformatorTransformatoren mit Ringkernen haben einen besonders hohen Wirkungsgrad, da aufgrund der geschlossenen Ringkernform nur geringe Streufeld-Verluste entstehen und der Eisenweg ein Minimum beträgt. Auch Ringkerne bestehen aus einzelnen Blechlagen, die durch ein ringförmig aufgewickeltes Band gebildet werden. Ringkerntransformatoren können mit höherer magnetischer Flussdichte und geringeren Hystereseverlusten arbeiten, wenn texturierte Blechbänder verwendet werden. Auch das trägt maßgeblich zur Verringerung der Baugröße bei. Außerdem können Ringkerne auch aus Ferriten hergestellt werden. Ringkerne werden auch für Stelltransformatoren verwendet, bei diesen kontaktiert ein drehbar gelagerter Schleifer die einzelnen Spulenwindungen. Zur Kontaktgabe für den Schleifer sind die Windungen der Spule an den Außenseiten freigelegt, d. h. die Lack-Isolation der Lackdrähte wird abgeschliffen. Trotz ihrer Vorteile kommen Ringkerntransformatoren nicht generell zum Einsatz, weil u. a. die Bewicklung eines geschlossenen Ringkerns aufwendiger ist. Eine Kompromisslösung stellen Schnittbandkerne dar: ein Blechband (Dicke 0,025–0,3 mm) wird auf einen Dorn mit rechteckigem Querschnitt aufgewickelt und verklebt. Anschließend wird der Wickel in der Mitte quer zerteilt und die Trennflächen werden poliert. Die Hälften werden dann in die bewickelten Spulenkörper gesteckt und verklebt. Für Schnittbandkerne werden teilweise auch texturierte Blechbänder eingesetzt. Schnittbandkerne haben ähnlich gute Eigenschaften wie Ringkerne, jedoch ist die Wicklungsherstellung einfacher. Dagegen ist die Kernherstellung etwas teurer (Baureihen SM, SE, SU, SG, S3U siehe auch DIN 41309 und IEC 329). Ring- und Schnittbandkerntransformatoren haben aufgrund ihres minimierten Eisenvolumens höhere Einschaltströme als andere Netztransformatoren, da sie dabei eher in die Sättigung geraten. Bei der Auslegung des Eisenkerns und der Windungszahl n sind folgende Zusammenhänge unter bestimmten Randbedingungen (sinusförmige Spannungsform, homogener luftspaltloser magnetischer Kreis) gültig:
mit
Die maximale Flussdichte liegt bei Eisen je nach Spezifikation bei 1,5…2 T. Bei Ferriten liegt sie bei etwa 200 mT. Mit Zunahme der Frequenz sinkt die Zahl der erforderlichen Transformatorwindungen und die Baugröße, weshalb sich Trafos für höhere Frequenzen sehr kompakt bauen lassen bzw. höhere Leistungen übertragen können (Beispiel: Schaltnetzteile). Die Verdoppelung der Frequenz ermöglicht bei einer gegebenen Baugröße – abgesehen von steigenden Kernverlusten – die Verdoppelung der übertragbaren Leistung. Für gleiche Spannungen müssen dafür die Querschnitte der Wicklungsdrähte verdoppelt werden, die erforderlichen Windungszahlen halbieren sich. Das Foto eines elektronischen Vorschaltgerätes (EVG) einer Energiesparlampe oben rechts zeigt einen Ferrit-Ringkerntransformator zur Ansteuerung der Schalttransistoren mit nur drei bzw. fünf Windungen. Kleine Ferrit-Transformatoren werden u. a. in Schaltnetzteilen und elektronischen Transformatoren für Niedervolt-Halogenglühlampen verwendet. DrehstromtransformatorenDreiphasenwechselspannung lässt sich mit drei gleichen Einphasentransformatoren übertragen. In der praktischen Ausführung werden jedoch überwiegend die drei getrennten Eisenkerne zu einem gemeinsamen Kern mit drei Schenkeln zusammengefasst. Für das einfachere Verständnis kann man sich die drei Kernschenkel an sich sternförmig angeordnet vorstellen. Die praktische Ausführung vereinfacht das abermals dahin, dass die drei Schenkel in einer geraden Linie hintereinander angeordnet werden und oben und unten mit einem gemeinsamen Eisenblech-Joch verbunden werden. Drehstromtransformatoren werden mit Nennleistungen von etwa 100 VA bis 1.100 MVA gebaut. Die Formel für das Übersetzungsverhältnis ü = n1 / n2 gilt für Drehstromtransformatoren nur bei gleicher Schaltung von Ober- und Unterspannungsseite wie etwa bei der Schaltgruppe Yy0. Die drei Phasenleiter der elektrischen Spannung werden üblicherweise in Europa mit den Buchstaben „L1“, „L2“ und „L3“ bezeichnet (früher als „R“, „S“ und „T“), die drei Wicklungsstränge von Drehstrommotoren und -transformatoren mit „U“, „V“ und „W“. Bei besonders großen Transformatoren können zur besseren Transportierbarkeit drei Einphasentransformatoren zu einer „Drehstrombank“ zusammengesetzt werden. Hierbei müssen jedoch die Stufenschalter und viele Meldeeinrichtungen jeweils dreifach vorhanden sein, so dass diese Anordnung eher selten ausgeführt wird. Mit Hilfe der sog. Scott-Schaltung wird der dreiphasige Drehstrom in ein zweiphasiges System gewandelt. Diese Art der Transformatoren wird gerne bei Heizungen eingesetzt, um eine symmetrische Belastung des Netzes zu erreichen. Auslegung der SpulenwicklungenWie schon oben erwähnt, ist die Ausgangsspannung der Transformator-Sekundärspule theoretisch exakt so groß, wie es das Windungszahlverhältnis zwischen den Wicklungen und die Primärspannung vorgeben. Es gilt: mit
Dies gilt jedoch nur für den Leerlauf bzw. den unbelasteten Zustand. Sobald in der Sekundärspule ein Strom zu einem äußeren Verbraucher fließt, teilt sich die Leerlaufspannung auf die inneren elektrischen Widerstände des Transformators und des Verbrauchers auf. Die Streuinduktivität führt ebenfalls zu einer Verringerung der Spannung. Beispiel: Für einen Transformatortyp ist von der Größe und vom Material her ein Leistungsverlust bei der Übertragung von 10 % bekannt. Bei der vorgesehenen Nennleistung soll die Sekundärspule genau 240 Volt abgeben. Die Windungszahl wird daher für eine Leerlaufspannung von ausgelegt. Bei Nennleistung liefert die Sekundärspule dann eine Spannung von Ein Transformator kann statt einer einzelnen auch mehrere getrennte Sekundärwicklungen für unterschiedliche Spannungen oder für getrennte Stromkreise haben. Die Sekundärwicklungen können eine oder mehrere Anzapfungen haben: so kann man auch mit einem Transformator mit nur einer Sekundärwicklung mehrere unterschiedlich hohe Sekundärspannungen erhalten. Die Primärwicklungen können ebenfalls mehrere Anzapfungen haben; dann ist ein solcher Transformator für unterschiedlich hohe Primärspannungen geeignet, bei denen trotzdem auf identische Ausgangsspannungen transformiert wird. Beim Spartransformator ist nur eine einzige Wicklung mit einer oder mehreren Anzapfungen vorhanden – bei dieser Bauform ist nur Spannungsanpassung, jedoch keine galvanische Trennung zwischen Ein- und Ausgangsspannung gegeben. Sein Vorteil ist die bei gleicher Übertragungsleistung geringere Masse (Eisen- u. Kupfergewicht). Bei Netztransformatoren mit nur einer Wicklungskammer ist die Primärwicklung meist zuunterst gewickelt – bei niedrigeren Ausgangsspannungen schützt so der dickere Draht der Sekundärwicklung den dünnen Draht der Primärwicklung. Bei hoher Ausgangsspannung wird durch diesen Wicklungsaufbau die Isolation zum Kern erleichtert. Audio-Transformatoren (Übertrager und Ausgangstransformatoren) haben oft ineinander greifende (sog. verschachtelte) Wicklungen, um die Streuinduktivität zu verringern und so die Übertragung hoher Frequenzen zu verbessern. MittenanzapfungWird die Wicklung der Sekundärseite nach der Hälfte der Gesamtanzahl der Windungen aufgetrennt und nach Außen geführt, so wird dies als Mitten- oder Mittelanzapfung bezeichnet. Somit hat man drei zur Verfügung stehende Spannungen. Eine Variation dieser Mittenanzapfung erhält man, indem man zwei gegensinnig gewickelte Wicklungen mit gleicher Anzahl von Windungen auf die Sekundärseite aufbringt. Dadurch erhält man unter anderem zwei um 180° zueinander phasenverschobene Spannungen mit gleicher Amplitude und Frequenz. Anwendungen
SpannungsanpassungDie Spannungstransformation wird angewendet, um Spannungen auf den gewünschten Wert umzuformen (zu transformieren). Beispiel: 230 Volt aus dem öffentlichen Stromnetz in 12 Volt für eine Halogenlampe. Bei kleinen und mittleren Leistungen sind häufig die Wicklungen zusammen mit dem Kern in Gießharz vergossen. Zur reinen Spannungsanpassung (beispielsweise von 230 V auf 115 V) werden so genannte Spartransformatoren mit nur einer gemeinsamen Wicklung verwendet. Die veränderte Ausgangsspannung wird durch eine Anzapfung (falls sie kleiner als die Eingangsspannung sein soll) oder einen zusätzlichen Wicklungsanhang (für eine Spannung größer als die Eingangsspannung) gewonnen. Dabei muss der Transformator nur einen Teil der benötigten Leistung (im Beispiel 230/115 V die Hälfte zuzüglich der transformatoreigenen Verlustleistungen) übertragen und lässt sich entsprechend kleiner bauen. Klingeltransformatoren z. B. haben die Aufgabe, die für die Türklingel erforderliche Spannung von 8 Volt aus der Netzspannung von 230 V zu erzeugen, sie sind in der Regel kurzschlussfest ausgeführt und weisen besonders geringe Leerlaufverluste auf. Energietransport
Zur verlustarmen Energieübertragung in Hochspannungsleitungen werden Spannungen auf hohe Werte transformiert. Dabei wandelt der Maschinentransformator des Kraftwerkes die Generatorspannung, bei großen Kraftwerken etwa 10 kV bis 30 kV, auf die Hochspannung von etwa 110 kV bis 400 kV um, wodurch im Verbundnetz die Transportverluste geringer ausfallen und größere Leistungen übertragen werden können. Die Transformationsverluste sind bei Hochspannungstrafos vergleichsweise gering und liegen meist bei 0,1 % der übertragenen Leistung. Der geringere Strom auf der Hochspannungsseite bei konstanter übertragener Leistung führt dazu, dass weniger Verlustwärme am ohmschen Widerstand der Leitung entsteht. Allerdings ist der Strom auf Hochspannungsleitungen im Normalbetriebsfall relativ hoch und betragsmäßig sogar höher als bei niedrigeren Spannungsebenen wie dem Mittelspannungsnetz. Der Strom auf 400-kV-Leitungen liegt im Bereich von 1 kA pro Außenleiter, im Vergleich dazu auf 110-kV-Leitungen „nur“ in der Größenordnung von 500 A, jeweils im normalen Betriebsbereich. Der Grund für den Betrieb von Hochspannungsleitungen ist eine Steigerung der zu übertragenen Gesamtleistung zu erreichen und nicht den Leiterstrom auf Hochspannungsleitungen zu verringern. Bei richtiger Übertragungsspannung heben sich induktive und kapazitive Blindleistung auf (Wellenwiderstand Z = (240 ... 300) Ohm). Diese Aussage gilt jedoch nur beim Übertragen der so genannten natürlichen Leistung Pn. Für das Mittelspannungsnetz werden die Hochspannungen in Umspannwerken wieder auf 10 kV bis 36 kV zurücktransformiert. Zur Abführung der Verlustwärme bei großen Leistungstransformatoren werden diese als Öltransformator in Behälter eingebaut, die mit Transformatorenöl gefüllt sind. Die Kühlung durch das Öl wird gegebenenfalls mit Kühlrippen und Umwälzpumpen forciert (siehe Bild mit Leistungstransformatoren). Aufgrund der isolierenden Eigenschaften des Öls reicht die Lackisolierung der Kupferleiter je nach Spannung aus, um das Tränken bzw. den Verguss der Wicklungen mit isolierenden Stoffen entfallen zu lassen. Große Transformatoren hingegen enthalten immer Feststoffisolationskomponenten auf Zellulosebasis. Durch die Alterung des Öls und Wasseraufnahme der Zellulose werden die Isolationseigenschaften mit steigender Betriebszeit allerdings schlechter. In den 1970er Jahren bis Anfang der 1980er Jahre wurden daher oft die giftigen, jedoch stabileren polychlorierte Biphenyle (PCB) verwendet. Die Spannungsanpassung bei Netz-Belastungssschwankungen und die Abstimmung beim Parallelschalten großer Leistungstransformatoren geschieht über mit in den Kessel eingebaute Stufenschalter. Zu diesem Zwecke sind die entsprechenden Wicklungen mit Anzapfungen versehen. Im Bild sind oberhalb des Transformators die drei gießharzisolierten, zylinderförmigen Rundsteuer-Einspeisetransformatoren erkennbar, die in Reihe zur unterspannungsseitigen Wicklung liegen und das nachgeschaltete Netz mit tonfrequenten Steuerimpulsfolgen der Rundsteueranlage beaufschlagen. Getaktete Netzteile / SchaltnetzteilAn Netzfrequenz mit 50 bzw. 60 Hz arbeitende Netztransformatoren sind relativ groß und schwer. Da die Änderungsgeschwindigkeit der Magnetfeldstärke die in den Wicklungen induzierte Spannung bestimmt, kann ein bei höherer Frequenz betriebener Transformator auch mehr Leistung übertragen. Mit steigender Frequenz kann die Windungszahl und/oder der Kernquerschnitt (Kernvolumen) abnehmen, ohne dass sich die Spannung verändert; siehe Formel (2). In Schaltnetzteilen werden zu diesem Zweck mit Halbleiterschaltern für den Transformator Eingangsspannungen mit Frequenzen von etwa 20 kHz bis 2 MHz erzeugt. Damit können erheblich leichtere Netzteile bzw. Stromversorgungen gebaut werden. Die Transformatorkerne von Schaltnetzteilen werden zur Verringerung der Hysterese- und Wirbelstromverluste meist aus Ferrit (ferromagnetische Keramik) oder aus Eisenpulver gefertigt. Auch die Wicklungen werden bei höheren Frequenzen wegen des Skineffektes häufig als flaches Kupferband oder mittels Hochfrequenzlitze (parallelgeschaltete dünne Drähte) ausgeführt. Trotz der gegenüber Eisen geringeren Sättigungsinduktion von Ferriten ist die Verringerung der Masse erheblich. Ein zur Übertragung von 4000 Watt geeigneter Transformator wiegt beispielsweise:
Die schnellen Strom- und Spannungsänderungen der Schaltnetzteile führen zu Hochfrequenz-Störungen, die meist mit Netzfiltern, Abschirmungen und Ausgangsfiltern verringert werden müssen. Mittelfrequenz-TransformatorenDie Formel für den Zusammenhang zwischen Windungszahl, Eisenquerschnitt und Spannung lautet
Auf den Eisenquerschnitt umgestellt zeigt sich, dass der Eisenquerschitt mit zunehmender Frequenz kleiner bemessen werden kann: Für bestimmte Anwendungsfälle wird daher eine höhere als die übliche Netzfrequenz verwendet, um kleinere Transformatoren zu bauen. Beispiele sind u. a.:
Gegenüber einer Betriebsfrequenz von 50 Hz sind dabei große Gewichtseinsparungen erreichbar. Bei Frequenzen bis zu einigen kHz („Mittelfrequenz“) können Leistungs-Transformatoren noch mit geblechten (Eisen-)Kernen gefertigt werden, doch muss die Blechdicke zur Vermeidung höherer Wirbelstromverluste geringer sein (etwa 0,1 mm gegenüber etwa 0,5 mm bei 50 Hz). Die Hystereseverluste halten sich dann noch in Grenzen. Galvanische TrennungAus sicherheitstechnischen Gründen (u. a. Blitzschlag) wird ein Anschluss der öffentlichen Stromversorgung auf Erdpotenzial bezogen. Um nun unter allen Umständen (z. B. zwischengeschaltete Kabel) zu verhindern, dass eine frei zugängliche, leitende Stelle des Gerätes Netzpotenzial führt und damit für den Benutzer die maximale Schutzkleinspannung überschritten wird, muss eine galvanische Trennung mit verstärkter Isolation oder eine Schutzerdung leitfähiger berührbarer Teile vorgenommen werden. Transformatoren mit getrennten, voneinander isolierten Wicklungen bieten diese galvanische Trennung. Die so genannte „sichere elektrischen Trennung“ (Schutzklasse II) ist in Normen (IEC, VDE, UL) definiert und verlangt besonders hohe elektrische Isolationsfestigkeit zwischen Primär- und Sekundärseite. Dafür geeignete Transformatoren haben oft getrennte, gekapselte Isolierstoff-Kammern für die Primär- bzw. Netzspannungswicklung. Aus einem geerdeten Netz kann man mit so genannten Trenntransformatoren (Übersetzungsverhältnis 1:1) ein gegen Erde isoliertes Netz schaffen. In Krankenhäusern ist eine solche Netztrennung für viele Geräte gefordert. Bei einem Körperschluss an einem Gerät, das mit Menschen in Kontakt kommt, kann so kein Erdstrom fließen. Vielmehr wird das Netz überwacht und der Fehler kann behoben werden. Eine Abschaltung ist nicht nötig solange kein zweiter Fehler auftritt. Reparaturarbeiten an netzbetriebenen Geräten (z. B. Fernseher) müssen ebenfalls an mittels Trenntransformator isolierter Netzspannung stattfinden. Gegen die Berührung der Bildröhren-Anodenspannung von 17 ... 27 kV bieten übliche Trenntransformatoren jedoch keinen Schutz: selbst ohne Berührung kann man bei Annäherung innerhalb der Schlagweite einen Stromschlag erleiden, da die Isolationsfestigkeit eines üblichen Trenntransformators nur etwa 4 kV beträgt. MesswandlerFür die Messung hoher Wechselströme und -spannungen werden Messwandler verwendet, mit denen die Spannung bzw. der Strom auf niedrige und für das Messgerät konforme Werte heruntertransformiert werden. Als Durchsteckwandler ausgeführte Stromwandler bestehen nur aus der Sekundärspule und dem Kern (Zangenamperemeter). Die Primärwicklung wird durch eine durchgesteckte Leitung des Leistungsstromkreises gebildet. Die Leitung kann ggf. auch mehrmals durch den Messwandler geführt werden, um den Messbereich gemäß den folgenden Formeln anzupassen:
Besonders hohe Anforderungen werden an Mess-Stromwandler und -spannungswandler für Energiezähler gestellt. Mit ihnen transformiert man den zu messenden Primärstrom auf die z. B. für 5 A ausgelegte Stromspule eines mechanischen Zählers oder man erzeugt mit einem an der Sekundärwicklung angeschlossenen Lastwiderstand eine kleine Messspannung für die Auswerteelektronik eines elektronischen Zählers. Durch die Verwendung spezieller Legierungen für den Kern sind gute Linearität und ein geringer Phasenfehler erreichbar. WiderstandstransformationEine Widerstandstransformation wird angewendet, um Verbraucher und Quellen hinsichtlich ihres Widerstandes oder Wellenwiderstandes anzupassen, zum Beispiel eine Ferritantenne an die Eingangsstufe des Radios oder einen Lautsprecher mit einer Impedanz von 4 Ohm an den Ausgang eines Röhrenverstärkers mit einer Impedanz von 1000 Ohm. Bei Transformation auf den gleichen Wert wird die maximal mögliche Leistung übertragen (Leistungsanpassung). Für den elektrischen Widerstand R einer Baugruppe gilt das ohmsche Gesetz Wendet man diese Beziehung auf die Primär- und Sekundärwicklung eines Transformators an, so folgt Für das Verhältnis von Primär- und Sekundärwiderstand errechnet sich daraus mit U~N und I~1/N das erforderliche Verhältnis der Windungszahlen: Durch ein Windungszahlverhältnis von 2 zu 1 wird also eine Widerstandstransformation von 4 zu 1 erreicht. Durch die Umrechnung des Widerstandes kann man beide Widerstände im Längszweig des Ersatzschaltbildes nun von nur einer Seite betrachten. Die Impedanz auf der nicht interessierenden Seite ist nun auf die Bezugsspannungsebene umgerechnet. Durch die Summe erhält man die Kurzschlussimpedanz. Alle Leistungs- und Kurzschlussberechnungen sind damit auf eine Spannung bezogen. ModellbetrachtungenElektrotechnische Definition idealer Übertrager
Ein idealer Transformator (Übertrager) ist ein elektrischer Vierpol mit den Eingangsgrößen
u1(t) und i1(t), den Ausgangsgrößen u2(t) und
i2(t) sowie dem Übertragungsfaktor Die Größen u1(t) und i1(t) heißen Primärgrößen des Transformators. Die Größen u2(t) und i2(t) heißen Sekundärgrößen des Transformators. Für γ > 0 heißt der Transformator „gleichsinnig gewickelt“, für γ < 0 heißt er „gegensinnig gewickelt“. Definitionsgleichungen bei komplexer RechnungBei Zeigerrechnung lauten die Gleichungen entsprechend ErläuterungDie Begriffe Transformator bzw. Übertrager können einerseits ein elektrotechnisches Bauelement bedeuten oder ein Modell dieses Bauelements. Die Bedeutung ergibt sich jeweils aus dem Zusammenhang. Der Übertragungsfaktor γ des Modells ist zunächst eine reelle Zahl, die als Parameter eines reinen Netzwerkmodells keine direkte physikalische Bedeutung hat. Modelliert man reale Transformatoren mithilfe des Modells des idealen Transformators, so entspricht der Faktor γ dem Wicklungsverhältnis Die Indizierung γ = n1 / n2 (statt der intuitiveren Reihenfolge: γ = n2 / n1) entspricht der Konvention in der einschlägigen Literatur. In der deutschsprachigen Literatur wird anstelle von γ häufig der Buchstabe Beide Seiten des Transformators werden im Verbraucherzählpfeilsystem aufgezeichnet. Diese Konvention ist physikalisch nicht intuitiv, da die Primärseite des Transformators hinsichtlich des folgenden Netzwerk meistens die Rolle eines Erzeugers spielt. Die Darstellung wurde gewählt, um eine mit der allgemeinen Zweitortheorie (früher: Vierpoltheorie) übereinstimmende Darstellung zu gewährleisten. Zur Vermeidung der negativen Vorzeichen in den Formeln wird in der Praxis die Sekundärseite des Transformators häufig abweichend von der hier gewählten Konvention im Erzeugerzählpfeilsystem bepfeilt. Das Modell des idealen Transformators berücksichtigt die wesentlichen Eigenschaften, wegen derer Transformatoren eingesetzt werden und vernachlässigt Randeffekte, die in der Praxis zusätzlich zu berücksichtigen sind. Er wird außerdem zur Modellierung realer Transformatoren verwendet. Insofern stellt das Modell ein effektives Mittel zur Analyse und Synthese elektrischer Transformatorschaltungen dar. Das ideale Modell erlaubt in dieser Form auch die Wandlung von Gleichgrößen. Das ist bei einem realen Transformator natürlich nicht möglich. Transformatoren werden allgemein zur Energiewandlung und speziell zur Spannungstransformation, zur Stromtransformation oder zur Widerstandstransformation eingesetzt. EnergiewandlungDer ideale Transformator ist ein reiner Energiewandler ohne Energiespeicher.
Die primärseitig in den Transformator eingespeiste Leistung Das negative Vorzeichen ist notwendig, da beide Transformatorseiten der inzwischen üblichen Konvention entsprechend im Verbraucherzählpfeilsystem bepfeilt sind, die Sekundärseite jedoch als Erzeuger aufgefasst wird. Die Leistungsbilanzgleichung ist die Grundlage für die Strom-, Spannungs- und Widerstandstransformation eines Transformators. Sie wird bei einem realen Transformator nur näherungsweise erreicht. In der Zeigerrechnung lautet die Leistungsbilanz: Hierbei deutet der Stern * an, dass das Konjugiert-Komplexe der bezeichneten Größe zu verwenden ist. Da Spannungs- und StromtransformationAus den Definitionsgleichungen ergibt sich unmittelbar: Auf der Seite mit dem höheren Strom herrscht also die geringere Spannung und umgekehrt. Beim realen Transformator gilt entsprechend: Auf der Seite mit der hohen Wicklungszahl herrscht die hohe Spannung und der kleine Strom. WiderstandstransformationBeschaltet man die Sekundärseite des Transformators mit einer Impedanz Mithilfe der Transformationsgleichungen ergibt sich für das Verhältnis von Primärspannung zu Primärstrom: Das Verhältnis von Primärspannung und Primärstrom ist die Impedanz, die der Transformator zusammen mit der sekundärseitigen Impedanz Beispiele zur Widerstandstransformation und Leistungsanpassung
1. Eine Wechselspannungsquelle Dem Windungsverhältnis entsprechend gilt
Entsprechend dem Wicklungsverhältnis beträgt der Primärstrom somit:
Die Spannung erhöht sich bei der Transformation um den Faktor 3, der Strom vermindert sich um den Faktor 3. Daher „sieht“ die Quelle U1 nur ein neuntel der auf der Sekundärseite anliegenden Impedanz. 2. Eine Spannungsquelle mit dem Innenwiderstand Die Last R beträgt auf der Primärseite nur R/9. Um Leistungsanpassung zu gewährleisten, muss Auf der Seite mit den hohen Wicklungszahlen ist demnach nicht nur die hohe Spannung, sondern auch der hohe Widerstand. Reale TransformatorenEin realer Transformator besteht typischerweise aus zwei oder mehr Spulen bzw. Leiterschleifen, die magnetisch eng gekoppelt sind. Das rechte Bild zeigt eine Anordnung aus zwei Spulen mit den Induktivitäten L1 und L2, die mit dem Kopplungsfaktor M miteinander magnetisch verkoppelt sind. Im Idealfall gelten die folgenden Bedingungen:
Die physikalische IdeeSind n1 und n2 die Wicklungszahlen der Spulen auf Primär- und Sekundärseite und herrscht in beiden Spulen derselbe magnetische Fluss Φ, so gilt mithilfe des Induktionsgesetzes: Ist der magnetische Fluss Φ konstant, so sind beide Gleichungen identisch null. Der Transformator überträgt keine Energie. Liegen Wechselgrößen vor, so kann man für alle Zeiten t mit Diese einfache Gleichung gilt jedoch nur für ideal gekoppelte Spulen ohne weitere parasitäre Effekte. Der verlustlose TransformatorDie Voraussetzung, dass die magnetische Flussdichte in beiden Teilspulen identisch ist, wird wegen des endlich großen magnetischen Widerstands des Magnetmaterials und der nicht ganz idealen Ausführung der Wicklungen nur näherungsweise erreicht. Das nebenstehende Bild zeigt die Zählpfeile der verwendeten Größen und den Richtungssinn der Spulenwicklungen. Der Zählpfeil Φ soll für alle magnetischen Flüsse gleichermaßen gelten. Er ist rechtshändig mit den entsprechenden Strömen gekoppelt. Nimmt man gleichsinnig gewickelte Spulen an und bezeichnet man mit
so herrschen in Primär- und Sekundärspule die Flüsse
Nach dem Induktionsgesetz gilt dann: Mithilfe der Selbstinduktivität L1 der Primärspule, der Selbstinduktivität L2 der Sekundärspule und der Koppelinduktivitäten M12 bzw. M21 kann die Magnetfelder über die zugehörigen Ströme auf Primär- und Sekundärseite ausdrücken. Dabei wird implizit der Durchflutungssatz angewendet. Es ergibt sich: Die Koppelinduktivitäten M12 und M21 sind identisch, so dass man den gemeinsamen Buchstaben M: = M12 = M21 verwenden kann. Es ergibt sich: Durch eine Laplacetransformation mit s = jω geht d / dt in jω über, und es ergibt sich in Zeigerrechnung: Diese Gleichungen bilden die Grundlage für das Ersatzschaltbild mit stromgesteuerten Spannungsquellen. Das Ersatzschaltbild mit gesteuerten Spannungsquellen kann in ein Ersatzschaltbild mit einem idealen Transformator überführt werden. Dabei ist Lσ1 die Streuinduktivität der Primärseite, Lσ2 die Streuinduktivität der Sekundärseite und Lh1 die Hauptinduktivität der Primärseite. Die Hauptinduktivität Lh1 wirkt wegen der Übertragungseigenschaften des idealen Transformators sowohl auf der Primär- als auch auf der Sekundärseite. Für die Induktivitäten gilt:
definiert, wobei k bei gleichem Wicklungssinn positiv und bei gegensinnigem Wicklungssinn negativ ist. k = 1 bedeutet perfekte Kopplung in dem Sinne, dass das gesamte Feld der Primärspule in die Sekundärspule eindringt. k = − 1 bedeutet ebenfalls eine perfekte Kopplung, jedoch sind die Wicklungen gegensinnig. k = 0 bedeutet, dass Primär- und Sekundärspulen magnetisch nicht gekoppelt sind, das heißt, das Feld der Primärspule tritt nicht in die Sekundärspule ein, und umgekehrt tritt das Feld der Sekundärspule nicht in die Primärspule ein.
Besonders einfach wird das Ersatzschaltbild, wenn man die Sekundärgrößen des idealen Transformators mithilfe der Formeln zur Spannungs-, Strom- und Widerstandstransformation auf die Primärseite transformiert: Abschließend soll eine verbale Beschreibung der verwendeten Bauelemente sowie die Betrachtung verschiedener Randbedingungen vorgenommen werden:
Der verlustbehaftete TransformatorEin realer Transformator weist Übertragungsverluste durch den ohmschen Widerstand der Wicklung und durch Ummagnetisierungsverluste (= Wirbelstrom- und Hystereseverluste) im Kern auf. Die Übertragungsverluste in den Wicklungen werden im Ersatzschaltbild durch die Wicklungswiderstände R1 und R2 von Primär- und Sekundärspule, die sogenannten Kupferverluste, berücksichtigt. Die Ummagnetisierungsverluste, häufig auch Eisenverluste genannt, sind Verluste, die im magnetischen Leiter (Ferritkern, Eisenkern) entstehen. Sie sind bei über die Luft gekoppelten Transformatoren nicht vorhanden. Es handelt sich dabei um die nichtlinearen Wirbelstromverluste und die ebenso nichtlinearen Hystereseverluste. Sie werden im Sinne einer einfachen Netzwerkberechnung in diesem Fall als das lineare Bauelement RFe (Fe für lateinisch „ferrum“, Eisen) modelliert. Nicht berücksichtigt ist in diesem Modell die kapazitive Kopplung zwischen Primär- und Sekundärseite, die durch die sich gegenüberstehenden Wicklungen von Primär- und Sekundärseite auftreten. Bei großen Transformatoren muss die Verlustleistung gegebenenfalls durch geeignete Kühlung abgeführt werden. Bei langdauernder Überlastung kann sich ein Transformator überhitzen, und die Isolation kann durchbrennen. Die Größen im Ersatzschaltbild haben die folgende Bedeutung:
Hystereseverluste und Wirbelstromverluste sind im Eisen begründet und werden deshalb als Eisenverluste bezeichnet. Die Stromwärmeverluste in den Wicklungen heißen Kupferverluste, da Transformatoren oft mit Kupferleitern gewickelt werden. Die Streuverluste ergeben sich aus den magnetischen Streuflüssen der Streuinduktivitäten. Sie wirken rein induktiv und verursachen einen Spannungsabfall, jedoch keine Wärme. Die Streuinduktivitäten sind maßgeblich verantwortlich für das Tiefpassverhalten eines Transformators. Die gestrichenen Größen im Ersatzschaltbild müssen entsprechend dem Übersetzungsverhältnis des Transformators (also dem Windungsverhältnis der beiden Spulen zueinander) umgerechnet werden:
Der reale Transformator als BandpassJeder reale Transformator weist dem Ersatzschaltbild entsprechend eine Bandpass-Charakteristik auf. Die Hauptinduktivität LH realisiert dabei den Hochpass, wobei Signale niedriger Frequenz über die Hauptinduktivität kurzgeschlossen werden. Die Streuinduktivitäten Lσ1 und Lσ2 realisieren den zugehörigen Tiefpass. Sie sind für Signale hoher Frequenzen hochohmig und verhindern ebenfalls eine Signalübertragung. Netztransformatoren für 50-Hz-Betrieb (USA: 60 Hz) weisen i. A. eine hohe Wicklungszahl auf. Bei niedrigen Frequenzen ist eine hohe Hauptinduktivität gewünscht, damit die Hauptinduktivität nicht als Kurzschluss wirkt. Hochfrequenztransformatoren beispielsweise im Amateurfunkbereich weisen oft nur geringe Hauptinduktivitäten auf. Wegen der sehr viel größeren Frequenzen sind bei Hochfrequenztransformatoren alle Induktivitäten deutlich hochohmiger als bei Netzfrequenztransformatoren, denn die Impedanz steigt entsprechend der Formel Der Innenwiderstand eines realen Transformators
Zur Berechnung des Innenwiderstands einer Quelle schaut man in Gedanken durch die Klemmen „von außen“ in die Quelle hinein und betrachtet, welcher Widerstand ein von außen eingeprägter Strom in der Quelle erfährt. Dabei werden ideale Spannungsquellen als Kurzschlüsse und ideale Stromquellen als Leerläufe angesehen. Beim Transformator ist zusätzlich die Widerstandstransformation des idealen Übertragers zu berücksichtigen. Bei der Berechnung wird angenommen, dass der Transformator primärseitig mit der Spannungsquelle Entsprechend dem Schaltbild ergibt sich der Innenwiderstand des realen Transformators als der Widerstand zwischen den Klemmen 2 und 2' zu: Hierbei bezeichnet γ den Übertragungsfaktor des Transformators mit Das Zeichen Transformatoren mit mehreren AnzapfungenVerlustursachen und spezielle EffekteWirbelstromverlusteDie Wirbelstromverluste entstehen durch das Induktionsgesetz: Durch die zeitliche Änderung des magnetischen Flusses ( = Flussdichte mal Kernquerschnitt) werden im elektrisch leitenden Kern Wirbelspannungen induziert. Mit diesen sind Wirbelströme verbunden, deren Größe durch die elektrischen Leitfähigkeit des Kernmaterials bestimmt wird. Das Produkt aus Spannung und Strom ergibt die den Kern erwärmende Wirbelstromverlustleistung. Zur Reduktion der Wirbelstromverluste verwendet man bei metallischen Werkstoffen geblechte Kerne. Dadurch bleibt die Länge des Wirbelstrompfads (= doppelte Kernbreite) groß, während der Fluss im einzelnen Blech ( = Flussdichte mal Blechquerschnitt) nun eine Wirbelspannung induziert, die umgekehrt proportional zur Anzahl der Bleche abnimmt und auch nur einen entsprechend kleinen Wirbelstrom hervorruft. Zur Widerstandserhöhung wird bei großen Transformatoren Elektroblech, eine Eisen-Silicium-Legierung mit hohem spezifischen elektrischen Widerstand, verwendet. Die bei hohen Frequenzen verwendeten Ferritkerne haben als keramische Werkstoffe eine um mehrere Größenordnungen kleinere elektrische Leitfähigkeit. Hystereseverluste
Hystereseverluste entstehen durch das Magnetisieren des Magnetmaterials. Ein Teil der Energie, die zur Verschiebung der Blochwände und für das Umklappen der Molekularmagnete erforderlich ist, geht irreversibel in Wärme über. Der Zusammenhang von B- und H-Feld kann nicht durch eine Funktion beschrieben werden, sondern durch eine geschlossene Kurve. Das Material weist ein „Gedächtnis“ auf. Bei jeder Magnetisierung entstehen Wärmeverluste, die dem Umlaufintegral zwischen B- und H-Kurve (d. h. der Fläche zwischen beiden Kurven) proportional sind. Die Hystereseverluste nehmen linear mit der Frequenz zu und zeigen eine starke Abhängigkeit vom maximal erreichten B. Sättigung des Kerns und ClippingKupferverlusteDie Kupferspulenwicklung besitzt einen ohmschen Widerstand, der als Wirkwiderstand mit dem Blindwiderstand der Spule in Reihe liegt. Durch diesen erwärmt sich der Draht bei Stromfluss. Die verlorene Leistung ist proportional zur Stromstärke im Quadrat. NachwirkungsverlusteDer im Eisen enthaltene Kohlenstoff nimmt je nach Richtung des Magnetfeldes bestimmte Zwischengitterplätze ein und stabilisiert die Blochwände. Damit sind die Blochwände bei weiteren Ummagnetisierungen schwerer zu bewegen. Skineffekt und Proximity-Effekt (Nahe-Effekt)Der Skineffekt tritt vorwiegend bei hohen Signalfrequenzen in Erscheinung. Er bewirkt, dass nur noch das Äußere des Leiters zum Stromfluss beiträgt. Der Skineffekt beruht auf der Abschirmungswirkung elektrisch leitfähiger Materialien gegenüber elektromagnetischen Feldern. Nach Küpfmüller, Mathis, Reibiger: Theoretische Elektrotechnik ist dieser Effekt nicht wie häufig beschrieben auf Wirbelströme zurückzuführen. Vielmehr handelt es sich um eine Felddiffusion in den Leiter, bei der die Eindringtiefe begrenzt ist und somit ein Eindringmaß definiert werden kann. Ein metallischer magnetisch neutraler Leiter wirkt für Hochfrequenzfelder wie ein magnetisch undurchlässiger Stoff mit der Permeabilität null. Der Skineffekt kann durch die Verwendung von Hochfrequenzlitze weitgehend unterbunden werden. Bei HF-Litze wird ein Leiter durch die Parallelschaltung von gegeneinander elektrisch isolierten und miteinander verwobenen Einzelleitern ersetzt. Der Proximity-Effekt beruht auf der Wechselwirkung des Stromes mit den elektromagnetischen Feldern benachbarter Leiter. Insbesondere dann, wenn benachbarte Leiter entgegengesetzt gerichtete Ströme aufweisen, sorgt der Proximity-Effekt für eine verminderte effektive Querschnittsfläche des Leiters. Siehe dazu auch: http://www.tu-dresden.de/etieeh/Lehre/vorlesungen_eet/Hochspannungsgeraete/G7.pdf BetriebszuständeLeerlauf bzw. „Unbelasteter Transformator“Wenn bei angelegter elektrischer Spannung an der Primärspule kein Strom aus der Sekundärspule des Transformators entnommen wird, wird dies als „Leerlauf“ oder „unbelasteter Betrieb“ bezeichnet. Im Leerlauf verhält sich die Primärspannung in sehr guter Näherung wie die Windungszahlen. Dabei sind In der Primärspule fließt bei Leerlauf dem T-Ersatzschaltbild entsprechend nur ein geringer Strom. Der Strom teilt sich auf in den Strom durch die Hauptinduktivität LH und den Strom über den Widerstand RFe. Der Strom über die Hauptinduktivität ist der Magnetisierungsstrom, der dem Durchflutungssatz Der größte Teil des Stromes auf der Primärseite fließt über den Widerstand RFe. Dieser Widerstand modelliert die Hystereseverluste und die Wirbelstromverluste (Eisenverluste). Hysterese- und Wirbelstromverluste sind weitgehend unabhängig von dem mit dem Transformator übertragenen Strom. Im Leerlauf kann man die Eisenverluste direkt messen, da die sonstigen Verluste wegen der nur geringen Ströme im Leerlauf vernachlässigbar klein sind. Der Transformator verhält sich im Leerlauf wie die Primärinduktivität L1. Es ist dabei belanglos, ob eine Sekundärspule vorhanden ist oder wie sie ausgeführt ist. KurzschlussbetriebDer Transformator befindet sich im Kurzschluss, wenn der Ausgang kurzgeschlossen wird, so dass Belasteter TransformatorIst der Transformator sekundärseitig belastet, so bewirkt der Sekundärstrom im Eisen ein zusätzliches magnetisches Wechselfeld. Nach der lenzschen Regel muss die durch den Sekundärstrom verursachte Magnetfeldänderung derjenigen, die durch den Primärstrom verursacht wird, entgegengerichtet sein. Die effektive Magnetfeldänderung ist bei Belastung somit in der Primärspule geringer als im unbelasteten Fall – die Flussdichte sinkt etwas. Dadurch wird auch die Selbstinduktionsspannung in der Primärwicklung Uip kleiner. Die Spannung an der Primärwicklung bleibt jedoch gleich, als Folge davon wächst der Primärstrom. Für die Scheinleistung S eines idealen (verlustfreien) Transformators gilt: Da S das Produkt aus Spannung U und Stromstärke I ist, gilt: und es folgt für die Beträge der Ströme: Da sich die Spannungen wie die Windungszahlen verhalten, verhalten sich folglich die Ströme (bzw. deren Beträge) umgekehrt wie die Windungszahlen: Der entnommene Strom wird also mit dem reziproken Windungszahlverhältnis auf die Primärseite transformiert. In kleinen Sekundärwindungszahlen lassen sich daher hohe Ströme erzeugen, sofern der Drahtquerschnitt ausreichend groß ist. Beispiel: Widerstandsschweißen. Nennlast-BetriebWenn an der Sekundärwicklung des Transformators die dauerhaft max. zulässige Leistung entnommen wird, heißt das, es wird Nennleistung entnommen, dies wird als Nennlastbetrieb bezeichnet. In diesem Fall liegt an der Sekundärspule die Nennspannung an. Die Nennspannung ergibt sich aus der Leerlaufspannung abzüglich der Spannung, die an den inneren Widerständen des Transformators abfällt, bzw. aufgebracht werden muss, um den Strom durch die Innenwiderstände zu treiben. Es ist: mit
Die Kurzschlussspannung ist die Spannung, die bei kurzgeschlossener Sekundärwicklung an der Primärwicklung liegen muss, damit die Primärwicklung den Nennstrom aufnimmt. Indem man diese bestimmt, kann man einen Transformator hinsichtlich seines Innenwiderstandes und seiner Effizienz testen und charakterisieren. Die Kurzschlussspannung ist eine Kenngröße von Leistungstransformatoren und wird in Prozent der Primär-Nennspannung angegeben. Sie soll in der Regel möglichst klein sein, damit auch bei hoher Last die Spannung an der Sekundärspule nur geringfügig abfällt. Bei Klingel- und Streufeldtransformatoren (Leuchtreklame, Schweißtransformator) ist die Kurzschlussspannung dagegen hoch, denn diese Transformatoren sollen kurzschlussfest sein bzw. dienen der Strombegrenzung. Eine weitere Ausnahme stellen Transformatoren bei Hoch- und Höchstspannungsnetzen (ab 220 kV) dar. Damit die Kurzschlussströme in diesen Netzen keine astronomisch hohen Werte annehmen liegen deren Kurzschlussspannungen ebenfalls etwas höher (8–15 %) Bei parallel geschalten Transformatoren gleicher Leistung sollten die Kurzschlussspannungen möglichst gleich sein, so dass der Trafo mit der kleineren Kurzschlussspannung nicht stärker belastet wird, als es dem Verhältnis der Nennleistungen entspricht. Lastbetrieb allgemeinBei Lastbetrieb wird das Übersetzungsverhältnis vom Leerlauf nicht mehr exakt eingehalten. Gründe sind:
Der durch die äußere Belastung fließende Strom in der Ausgangswicklung erzeugt einen entgegengesetzten magnetischen Fluss, dadurch wird das Magnetfeld der Eingangswicklung geschwächt. In die Eingangswicklung wird dadurch weniger Spannung induziert, was wiederum zu einer erhöhten Stromaufnahme führt. Der entgegengesetzt gerichtete magnetische Fluss bewirkt auch, dass der magnetische Fluss der Eingangswicklung als nicht nutzbarer Streufluss teilweise das Eisen verlässt und nicht die gesamte Sekundärwicklung durchdringt. Die Ausgangsspannung eines Transformators sinkt mit steigender Belastung ab. Die zur Induktion zur Verfügung stehende bzw. die induzierte Spannung verteilen sich zunehmend gemäß dem ohmschen Gesetz auch auf die ohmschen Widerstände der Kupfer-Wicklungen. Überlast und KurzschlussimpedanzWenn an der Sekundärwicklung des Transformators erheblich mehr als die Nennleistung entnommen wird, liegt der sog. Überlast-Betrieb vor. Dies führt zum Zusammenbruch der Sekundärspannung, diese verringert sich erheblich. Zunehmende Stromentnahme bedeutet Abnahme des Verbraucherwiderstandes, die Sekundär- bzw. Leerlaufspannung verteilt sich nun auf den Innenwiderstand des Transformators und den Verbraucherwiderstand zugunsten Ersterem: mit
Daraus folgt: mit
Wird – bei konstantem Innenwiderstand des Transformators – der Verbraucherwiderstand immer kleiner, dann verschiebt sich somit die Spannungsverteilung hin zu einem kleineren Anteil der Verbraucherspannung. Sind Uv und Ui gleichgroß, liegt sog. Leistungsanpassung vor, die Verlustleistung gleicht der Ausgangsleistung, die Leistungsabgabe des Transformators erreicht ihr Maximum, der Wirkungsgrad beträgt 50 %. Nur sehr kleine Transformatoren können dauernd in diesem Bereich betrieben werden, ohne thermisch überlastet zu werden. Bei höherer Stromentnahme auf der Sekundärseite wird zwangsläufig auch der Strom auf der Primärseite höher. Die Zunahme des Primärstroms bei Be- oder Überlastung führt im Eisenkern zu einer Verringerung der Erregerfeldstärke (nicht, wie oft fälschlicherweise angenommen, zu einer Erhöhung). Der Grund ist die durch den ohm'schen Spannungsabfall in der Primärwicklung verringerte wirksame Spannung. Dadurch sinkt auch der durch die Primärinduktivität bestimmte Blindstrom. Der höhere primärseitige Wirkstrom wird dagegen durch den Sekundärstrom kompensiert und trägt nicht zur Magnetisierung bei. Im Unterschied zu einem direkten Kurzschluss wirkt ein Transformator bei sekundärseitigem Kurzschluss primärseitig eher wie eine Drossel. Ein idealer Kurzschluss auf der Sekundärseite eines Transformators führt am Primäranschluss zu einer sich aus den Streuinduktivitäten und ohmschen Verlusten ergebenden Kurzschluss-Impedanz Zk: mit
Die Kurzschluss-Impedanz des Transformators verhält sich wie eine verlustbehaftete Induktivität, die jedoch wesentlich kleiner als die Eigeninduktivität der Primärseite im Leerlauffall ist. Auch bei guter Kopplung der Wicklungen hat die Kurzschluss-Impedanz einen signifikanten induktiven Anteil. Größere Transformatoren haben generell einen höheren induktiven Anteil der Kurzschlussimpedanz. Aus der Kurzschlussimpedanz lässt sich der Kurzschlussstrom Ik errechnen: Seine relative Größe kann durch Luftspalte, zusätzliche Schenkel im Kern, durch einen dünnen Kern und durch lockere Packung der Windungen (dünne Drähte, großer Abstand der Wicklungen voneinander und zum Kern) verringert werden, um die Kurzschlussfestigkeit zu erhöhen. Transformatoren, die typischerweise kurzzeitig überlastet betrieben werden, sind in Elektroloks, Lötpistolen und Punktschweißgeräten zu finden. Auch bei der elektrischen Stahlerzeugung mit Lichtbogenöfen werden besonders be- und überlastbare Transformatoren eingesetzt. Aufgrund der erheblichen Wärmeentwicklung bei fortdauerndem Überlastbetrieb droht Zerstörung der Isolation (Windungsschluss) oder sogar Brände und Explosionen durch die sich aus der Isolation entwickelnden Gase. Aus den magnetischen Kräften eines kurzgeschlossenen Transformators ergeben sich enorme mechanische Spannungen, durch die bei großen Transformatoren die Wicklungsdrähte zerreißen und nach außen geschleudert werden können. Die Kurzschlussspannung ist dagegen diejenige Spannung, die bei kurzgeschlossener Sekundärwicklung an der Primärwicklung liegen muss, damit die Primärwicklung den Nennstrom aufnimmt. Die Kurzschlussspannung ist eine wichtige Kenngröße von großen Transformatoren und wird in Prozent der Primär-Nennspannung angegeben. Parallelgeschaltete Transformatoren sollen sich hinsichtlich ihrer Kurzschlussspannung möglichst wenig unterscheiden, damit sie bei Belastung anteilige Leistung übertragen. EinschaltvorgangBeim Einschalten eines Transformators zu einem beliebigen Zeitpunkt kann es zu einem erhöhten Einschaltstrom kommen. Dabei wird der Kern in die Sättigung getrieben und kann nicht weiter magnetisiert werden. Durch die Sättigung des Kerns und die damit verbundene Reduktion des induktiven Blindwiderstandes können kurzzeitig sehr hohe Ströme fließen, welche unter Umständen das Ansprechen von Sicherungselementen bewirken können, insbesondere bei Ringkerntransformatoren. Die Höhe des Einschaltstromes hängt von dem Einschaltzeitpunkt im Bezug zum zeitlichen Verlauf der angelegten Wechselspannung und der im Transformatorkern gespeicherten magnetischen Flussdichte, der Remanenz BR, ab. Ist der Wert der Remanenz null, weil ein großer Luftspalt im Eisenkern liegt oder ein Lufttransformator verwendet wird, liegt der ideale Einschaltzeitpunkt bei dem Scheitelwert der speisenden Spannung. Dies kommt jedoch bei Transformatoren zur Energieübertragung praktisch nicht vor. Ist die Remanenz ungleich null verschiebt sich der ideale Einschaltzeitpunkt weg vom Scheitel der Spannung. Der richtige Einschaltzeitpunkt hängt also von der Polarität und der Höhe der gespeicherten Flussdichte, der Remanenz, ab, die wiederum vom Ausschaltzeitpunkt abhängt. Der richtige Einschaltzeitpunkt muss so gewählt werden, dass die Magnetisierung die Betriebs-Hysteresekurve nach dem Einschalten nicht verläßt. Der richtige Einschaltzeitpunkt kann bei verschiedenen Spannungsamplituden in der negativen oder positiven Spannungshalbwelle liegen, da beim Einschalten die Änderung der Magnetisierung immer von der Remanenz ausgeht. Da die Remanenz eines Transformators von außen nicht erkennbar ist, wurden in der Vergangenheit verschiedene Verfahren entwickelt die Remanenz zu beeinflussen, um einen Transformator sanft einschalten zu können. Normen und geltende Richtlinien für TransformatorenEin Transformator, der mit Spannungen bis 1000 Volt betrieben wird, darf innerhalb der Europäischen Union nur dann in den Handel und in den Betrieb gebracht werden, wenn er entsprechend der europäischen Niederspannungsrichtlinie beschaffen ist. In Deutschland wird dies mit der Anwendung der Ersten Verordnung zum Geräte- und Produktsicherheitsgesetz umgesetzt. Neben der allgemein für alle elektrische Geräte geltenden Niederspannungsrichtlinie muss ein Transformator in Europa noch mit weiteren spezielleren Regelungen übereinstimmen, speziell der jeweiligen nationalen Fassung der Norm EN 61558 IEC 61558. Die Übereinstimmung des Transformators mit den europäischen Richtlinien wird mit der CE-Kennzeichnung dokumentiert. Der Transformator kann dann ohne weitere Kontrollen und Prüfungen innerhalb der EU in den Verkehr gebracht werden. In Teil 1 der EN 61558 IEC 61558 werden allgemeine Anforderungen und Prüfungen beschrieben. Im Teil 2 sind die speziellen Transformatortypen wie z. B. Sicherheitstransformatoren (Teil 2–6) oder Schaltnetzteiltransformatoren (Teil 2–17) jeweils als eigene Norm aufgeführt, die sich jedoch auf Teil 1 für die grundlegenden Anforderungen beziehen. Deutsche DIN-Fassung der Europäischen Norm EN 61558 IEC 61558 (bzw. die entsprechenden VDE-Richtlinien-Dokumente) für Transformatoren sind:
Siehe auchSpezielle Transformatoren
Bestandteile und Zubehör
Kern: Magnetostriktion Quellen
Literatur
Kategorien: Lesenswert | Induktanz |
||
| Dieser Artikel basiert auf dem Artikel Transformator aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





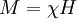
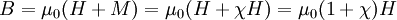
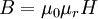
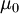 ist eine Naturkonstante, die absolute Permeabilitätskonstante.
ist eine Naturkonstante, die absolute Permeabilitätskonstante.
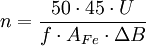
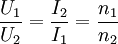
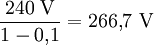
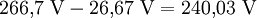
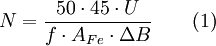
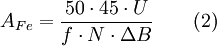
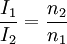 oder
oder 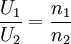 .
.
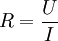
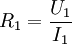
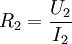
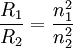
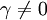 , für den gilt:
, für den gilt:
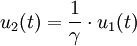
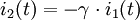
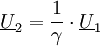
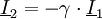
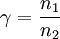 der Wicklungszahlen auf Primär- und Sekundärseite bzw. (in allgemeinerer Darstellung) der Wurzel
der Wicklungszahlen auf Primär- und Sekundärseite bzw. (in allgemeinerer Darstellung) der Wurzel 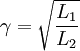 des Verhältnisses der Eigeninduktivitäten von Primär- und Sekundärspule. Dabei geht man jeweils von gleichsinnigen Wicklungen auf Primär- und Sekundärseite aus.
des Verhältnisses der Eigeninduktivitäten von Primär- und Sekundärspule. Dabei geht man jeweils von gleichsinnigen Wicklungen auf Primär- und Sekundärseite aus.
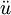 verwendet.
verwendet.
 ist zu jedem Zeitpunkt identisch mit der dem Transformator sekundärseitig entnommenen Leistung
ist zu jedem Zeitpunkt identisch mit der dem Transformator sekundärseitig entnommenen Leistung 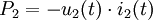 , so dass gilt:
, so dass gilt:
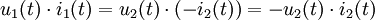
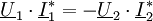
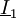 und
und 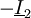 gemäß der Vereinbarung
gemäß der Vereinbarung 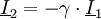 mit reellem
mit reellem 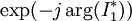 multiplizieren, so dass sich die folgende Vereinfachung ergibt:
multiplizieren, so dass sich die folgende Vereinfachung ergibt:
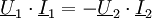
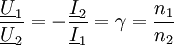
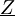 , so legt diese das Verhältnis von Sekundärspannung zu Sekundärstrom fest, und es gilt:
, so legt diese das Verhältnis von Sekundärspannung zu Sekundärstrom fest, und es gilt:
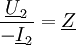
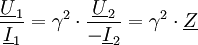
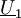 ohne Innenwiderstand treibt einen Transformator mit dem Wicklungsverhältnis 1:3 und dem sekundärseitigen Widerstand
ohne Innenwiderstand treibt einen Transformator mit dem Wicklungsverhältnis 1:3 und dem sekundärseitigen Widerstand 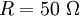 .
.
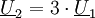 .
Nach dem Bauelementgesetz für den ohmschen Widerstand ergibt sich:
.
Nach dem Bauelementgesetz für den ohmschen Widerstand ergibt sich:
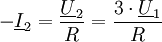 .
.
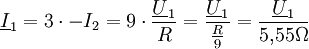 .
.
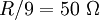 gelten, also
gelten, also 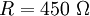 .
.
 kein Streufeld
kein Streufeld
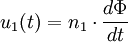
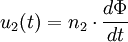
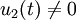 beide Gleichungen miteinander dividieren, und es ergibt sich:
beide Gleichungen miteinander dividieren, und es ergibt sich:
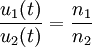
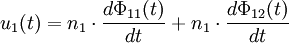
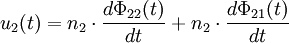
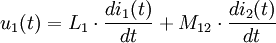
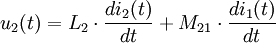
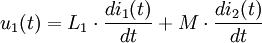
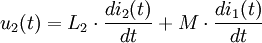
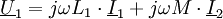
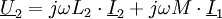
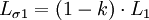
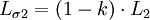
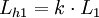
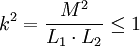
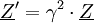
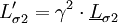
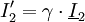
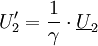
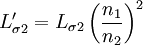 ,
, 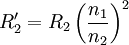 ,
, 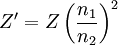
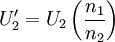 ,
, 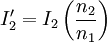
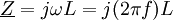 proportional mit der Frequenz
proportional mit der Frequenz 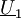 mit dem Innenwiderstand
mit dem Innenwiderstand ![\underline Z_{i} = \left( {1 \over \gamma} \right )^2 \cdot \left ( L^'_{\sigma2} + R^'_{2} + \left [R_{Fe} \parallel L_{h1} \parallel (R_1 + L_{\sigma 1} + R_{q1}) \right ] \right ) = L_{\sigma2} + R_{2} + \left({1 \over \gamma} \right )^2 \cdot \Big [R_{Fe} \parallel L_{h1} \parallel (R_1 + L_{\sigma 1} + R_{q1}) \Big ] \,](images/math/d/b/7/db7276a6870fa4488d2aede627603b2f.png)
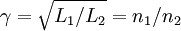 .
.
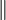 bedeutet die Parallelschaltung der betreffenden Impedanzen.
bedeutet die Parallelschaltung der betreffenden Impedanzen.
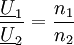
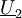 die Primär- und Sekundärspannung sowie n1 und n2 die Primär- und Sekundärwindungszahl.
die Primär- und Sekundärspannung sowie n1 und n2 die Primär- und Sekundärwindungszahl.
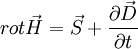 entsprechend für den Aufbau des H-Feldes im Magnetkern benötigt wird. In den meisten Anwendungen ist der Magnetisierungsstrom unerwünscht, da er nur indirekt zur Leistungs- bzw. Signalübertragung beiträgt. Der Magnetisierungsstrom ist umso geringer, je größer die Induktivität der Spulen auf Primär- und Sekundärseite ist und je größer die Signalfrequenz ist.
entsprechend für den Aufbau des H-Feldes im Magnetkern benötigt wird. In den meisten Anwendungen ist der Magnetisierungsstrom unerwünscht, da er nur indirekt zur Leistungs- bzw. Signalübertragung beiträgt. Der Magnetisierungsstrom ist umso geringer, je größer die Induktivität der Spulen auf Primär- und Sekundärseite ist und je größer die Signalfrequenz ist.
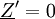 gilt.
Im Kurzschlussbetrieb wird der primärseitige Strom bei eingeprägter Spannung ausschließlich durch die Streuinduktivitäten
gilt.
Im Kurzschlussbetrieb wird der primärseitige Strom bei eingeprägter Spannung ausschließlich durch die Streuinduktivitäten