Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
WellengleichungAls Wellengleichung bezeichnet man eine partielle Differentialgleichung, deren Lösungen die Ausbreitung von Wellen modelliert. Darüber hinaus ist sie (zusammen mit zahlreichen Varianten) als unabhängiger Forschungsgegenstand von Interesse. Weiteres empfehlenswertes Fachwissen
Die homogene WellengleichungUnter einer homogenen Wellengleichung versteht man eine lineare partielle Differentialgleichung zweiter Ordnung für eine Funktion
im n-dimensionalen Raum der Form
Die Wellengleichung ist eine partielle Differentialgleichung vom hyperbolischen Typ. Oft wird der Begriff "Wellengleichung" darüber hinaus auch auf andere lineare Differentialgleichungen zweiter Ordnung angewendet, deren Lösungen als Linearkombinationen ebener Wellen geschrieben werden können. Die Funktion u kann dabei in die reellen oder komplexen Zahlen, aber auch auf Vektoren, Tensoren oder Spinoren abbilden. Lösungen der homogenen Wellengleichung in einer DimensionDie homogene Wellengleichung in einer Dimension lautet (hierbei ist die Funktion u natürlich zweidimensional, aber üblicherweise wird t hier nicht mitgezählt). Sie hat als allgemeine Lösung mit beliebigen zweimal differenzierbaren Funktionen f(x) und g(x). Dabei beschreibt der erste Summand eine mit Geschwindigkeit c nach links laufende, der zweite Summand eine mit derselben Geschwindigkeit nach rechts laufende ebene Welle. Mit Hilfe der Fouriertransformation lassen sich die Funktionen f und g als Linearkombination von Sinus-Funktionen oder auch komplexen Exponentialfunktionen schreiben, wobei diese Funktionen die Form bzw. haben (in der zweiten Schreibweise steckt die Phase φ im komplexen Vorfaktor A), wobei Lösung mit speziellen AnfangsbedingungenSei also Integration der zweiten Gleichung ergibt: Durch Auflösen erhält man: Die Lösung der Wellengleichung unter den obigen Anfangsbedingungen lautet demnach: Die Wellengleichung in mehreren DimensionenIn mehreren Dimensionen lässt sich die allgemeine Lösung nicht mehr so einfach hinschreiben, aber auch hier können alle Lösungen als Linearkombination der ebenen Wellen bzw. mit geschrieben werden. Diese Wellen haben alle die Geschwindigkeit c und bewegen sich in Richtung von Allgemeine WellengleichungIm allgemeinen (4-dimensionalen) Fall lautet die Wellengleichung
Dabei ist c die Ausbreitungsgeschwindigkeit und Δ der Laplaceoperator. Die Wellengleichung kann man mit dem d'Alembertoperator oder Quablaoperator ("Viereckoperator") vereinfacht als
Die Wellengleichung für elektromagnetische WellenDie Herleitung der Wellengleichung aus der TelegraphengleichungDie Herleitung der Wellengleichung findet unter Anwendung der maxwellschen Gleichungen in differentieller Form statt.
an dieser Stelle lassen sich mit Hilfe der Vektoranalysis bzw der Graßmann-Identität verschiedene Vereinfachungen vornehmen:
Für einen metallischen Leiter gilt somit:
Für einen Isolator gilt im materiefreien Raum (näherungsweise auch Luft) allerdings:
Wellengleichung für anisotrope KörperIn anisotropen Körpern ist die elektrische Feldstärke
Die Lösung dieser Gleichung ist Thema der Kristalloptik. Wellengleichung in kovarianter FormulierungIn der kovarianten Formulierung der Elektrodynamik lauten die inhomogenen Maxwellgleichungen:
wobei Die Herleitung ist also im 4er-Formalismus um einiges einfacher. Die Wellengleichung lautet also (sie ist im Übrigen Lorentz-invariant, allerdings nicht Galilei-invariant): Akustische Wellengleichung in Flüssigkeiten und GasenDie akustische Wellengleichung wird abgeleitet aus der Newtonschen Kraftgleichung in differentieller Form mit dem Druck p, der Dichte ρ und der Schallschnelle (Partikelgeschwindigkeit) Die zweite Grundgleichung ist die Kontinuitätsgleichung mit der Schallgeschwindigkeit Aus beiden Gleichungen zusammen folgt
die in der Form genau der elektromagnetischen Wellengleichung entspricht. Weil aber der Schalldruck p anders als die elektrische Feldstärke E eine skalare Größe ist, gibt es bei akustischen Wellen keine Polarisation. weitere Wellengleichungen
Kategorien: Quantenphysik | Elektrodynamik |
| Dieser Artikel basiert auf dem Artikel Wellengleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




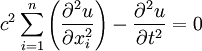 .
.
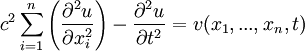 .
.
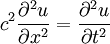
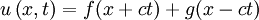
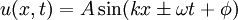
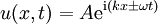
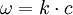
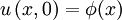 sowie
sowie 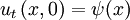 zwei Anfangsbedingungen, dann folgt:
zwei Anfangsbedingungen, dann folgt:
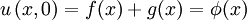
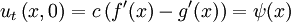
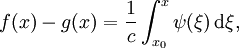
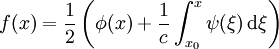
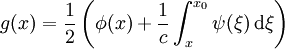
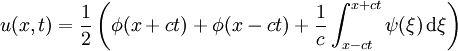
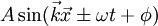
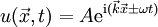
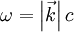
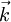 .
.
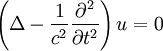 .
.
 schreiben.
schreiben.
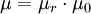
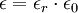
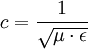 und im Falle
und im Falle 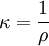 und entspricht der Leitfähigkeit (
und entspricht der Leitfähigkeit (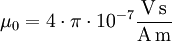 und
und 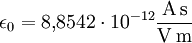
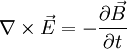 (Maxwell'sche Gleichung)
(Maxwell'sche Gleichung)
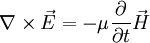
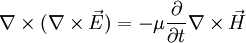 und mit
und mit 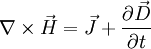 (Maxwell'sche Gleichung)
(Maxwell'sche Gleichung)
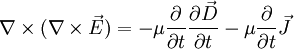 nun mit
nun mit 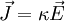
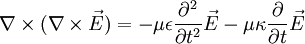
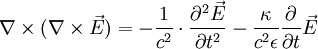 (vgl. hier auch die
(vgl. hier auch die 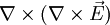 auch bekannt als rot rot E, kann umgeschrieben werden zu
auch bekannt als rot rot E, kann umgeschrieben werden zu
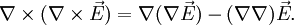
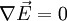 (Maxwell:
(Maxwell: 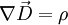 und der Raumladungsdichte
und der Raumladungsdichte 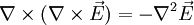
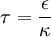 abklingt. (vergleiche auch die Elektrostatik)
abklingt. (vergleiche auch die Elektrostatik)
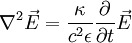 oder
oder 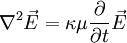
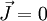
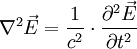 oder
oder 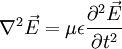
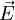 und die
und die 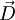 nicht mehr gleich gerichtet. Damit kann die
nicht mehr gleich gerichtet. Damit kann die 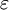 , welche die beiden Formelgrößen verknüpft, nicht mehr als Skalar aufgefasst, sondern muss als Tensor zweiter Stufe behandelt werden. Wie sich eine elektromagnetische Welle im anisotropen Medium ausbreitet, lässt sich durch Lösen der Wellengleichung für anisotrope Körper berechnen:
, welche die beiden Formelgrößen verknüpft, nicht mehr als Skalar aufgefasst, sondern muss als Tensor zweiter Stufe behandelt werden. Wie sich eine elektromagnetische Welle im anisotropen Medium ausbreitet, lässt sich durch Lösen der Wellengleichung für anisotrope Körper berechnen:
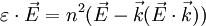
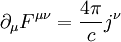 ,
,
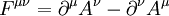 . In
. In 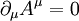 ergibt sich:
ergibt sich:
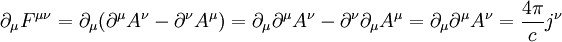
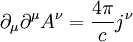
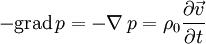
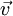 .
.
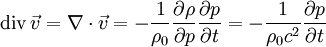
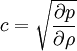 .
.
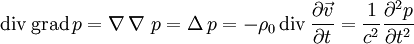 ,
,


