Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Maxwellsche GleichungenDie vier maxwellschen Gleichungen beschreiben die Erzeugung von elektrischen und magnetischen Feldern durch Ladungen und Ströme, sowie die Wechselwirkung zwischen diesen beiden Feldern, die bei zeitabhängigen Feldern in Erscheinung tritt. Sie sind die Grundlage der Elektrodynamik und der theoretischen Elektrotechnik und wurden in den Jahren 1861 bis 1864 von James Clerk Maxwell entwickelt. Im Wesentlichen fasste Maxwell die bis zu diesem Zeitpunkt entdeckten Gesetzmäßigkeiten
in einer vereinheitlichten Theorie zusammen und ergänzte sie um
um Konsistenz mit der Kontinuitätsgleichung zu erhalten. Somit sind die maxwellschen Gleichungen ein Standardbeispiel für eine vereinheitlichte Theorie, die verschiedene Phänomene, hier magnetische und elektrische, in einer geschlossenen Form erklären kann. Die maxwellschen Gleichungen wurden aus Erfahrungen und Experimenten entwickelt, daher ist die maxwellsche Theorie auch eine makroskopische Theorie. Produkt-HighlightÜbersichtFür das Verständnis der folgenden Gleichungen sind Grundkenntnisse in Vektoranalysis erforderlich. Die maxwellschen Gleichungen lassen sich in differentieller und in integraler Form darstellen. Die Äquivalenz beider Formulierungen beruht auf dem Satz von Stokes und dem Satz von Gauß. Daneben gibt es eine elegante vierdimensionale Formulierung, die sogenannte kovariante Form (s. u.), die z. B. in der Relativitätstheorie und der Quantenelektrodynamik verwendet wird.
Siehe auch: Differentielle und integrierte Form ErläuterungenSkalare FelderDas Symbol ρ steht dabei für die Raumladungsdichte und stellt die über den Raum verteilte elektrische Ladung dar. Die Verteilung der Ladung im Raum ist ein skalares Feld. VektorfelderOben eingeführte Vektorfelder lassen sich in drei Bereiche einteilen, welche durch ihren jeweiligen Satz von Gleichungen beschrieben werden. Diese drei Bereiche sind das elektrische Strömungsfeld, das elektrische Feld und das magnetische Feld. Elektrisches StrömungsfeldDie elektrische Stromdichte Elektrisches Feld
Magnetisches Feld
Die magnetische Polarisation ZusammenhangDie in allen drei Bereichen auftretenden Materialgleichungen werden nicht direkt zu den maxwellschen Gleichungen gezählt, sondern die drei Gleichungssätze:
stellen gemeinsam und unter gegenseitiger Ergänzung das Fundament der elektrodynamischen Feldtheorie dar. Die Materialgleichungen gelten in der allgemeinen Form sowohl für den leeren Raum als auch für mit Materie ausgefüllte Raumbereiche. Aus historischen Gründen und manchmal auch um bestimmte Berechnungsvorgänge spezifisch darzustellen, werden die Materiegleichungen und die darin auftreten drei Leitfähigkeiten jeweils in den Anteil des leeren Raumes Für das elektrische Feld ergibt sich durch die Aufspaltung der dieelektrischen Leitfähigkeit die Möglichkeit zur Einführung eines weiteren Vektorfeldes, der elektrischen Polarisation Analog dazu beschreibt die magnetische Polarisation Grundsätzlich kann ohne Verlust auf die Einführung der Vektorfelder der elektrischen Polarisation Maxwellgleichungen in MaterieIn Materie gilt allgemein:
wobei sich im Spezialfall der Linearität bei Isotropie oder bei kubischen Systemen noch folgende Vereinfachung ergibt
In anisotroper nicht-kubischer linearer Materie werden die Skalare Die dielektrische Polarisation ist dann mit der elektrischen Suszeptibilität χe, bzw. der relativen Permittivität
Für die magnetische Polarisation
(Vorsicht: im cgs-System sind χe und χm mit 4π zu multiplizieren!) Weiter ergibt sich die Definition der Brechzahl mit
was die Lichtgeschwindigkeit im Material mit den entsprechenden Konstanten in Verbindung bringt. So ist die Phasengeschwindigkeit im Medium
die bei frequenzunabhängiger Brechzahl (ohne Dispersion) gleich der Gruppengeschwindigkeit im Medium ist. Maxwellgleichungen für konstante Frequenzen ω in komplexer SchreibweiseDie in den maxwellschen Gleichungen auftretenden Feldvektoren sind im allgemeinen nicht nur Funktionen des Ortes sondern auch der Zeit, beispielsweise Mit Hilfe der komplexen Schreibweise lässt sich die Zeitabhängigkeit bei harmonischen Vorgängen vermeiden, da sich der komplexe Zeitfaktor ejωt dabei heraushebt. Die in den maxwellschen Gleichungen auftretenden Feldgrößen sind dann komplexe Amplituden und nur noch Funktionen des Ortes. An Stelle der partiellen Differentiation nach der Zeit tritt die Multiplikation mit dem imaginären Faktor jω. ω wird auch als Kreisfrequenz bezeichnet. In komplexer Form, komplexe Größen sind zur Unterscheidung unterstrichen, lauten die maxwellschen Gleichungen in Differentialform: Kovariante Formulierung der Maxwellgleichungen
Die Elektrodynamik, wie sie durch die Maxwellgleichungen beschrieben wird, ist im Gegensatz zur newtonschen Mechanik verträglich mit der speziellen Relativitätstheorie. Dazu gehört, dass die Maxwellgleichungen in jedem Inertialsystem gelten, ohne dass sich beim Wechsel des Bezugssystems ihre Form ändert. Dies spielte historisch für die Entwicklung der Relativitätstheorie durch Albert Einstein eine wichtige Rolle. Technischer formuliert sind die Maxwellgleichungen relativistisch kovariant oder forminvariant, das heißt, dass sie ihre Gestalt unter Lorentz-Transformationen nicht ändern. Diese Eigenschaft ist den Maxwellgleichungen in der oben beschriebenen Form jedoch nicht ohne weiteres anzusehen. Es kann deshalb nützlich sein, durch eine Umformulierung der Theorie die Forminvarianz herauszuarbeiten, anders ausgedrückt: die Theorie „manifest kovariant“ zu schreiben. Hierzu ist es zweckmäßig, die oben auftretenden Größen
erhält (siehe auch Elektrodynamik). Diese Größen lassen sich zu einem Vierervektor, dem Viererpotential zusammenfassen. Ebenso kann man aus Ladungsdichte ρ und Stromdichte
Man definiert nun den Vierergradienten, die relativistische Form der Ableitung, als
Mit diesen Größen kann man die beiden inhomogenen Maxwellgleichungen im Vakuum durch die kovariante Gleichung ersetzen. Dabei wird, wie üblich, die einsteinsche Summenkonvention benutzt, das heißt, über doppelt auftretende Indizes in Produkten (hier α) wird summiert. Ferner erfolgt wie üblich das Herauf- und Herunterziehen von Indizes mit dem Tensor
Dies wird auch häufig mit dem Levi-Civita-Symbol kompakter geschrieben als oder mit dem dualen Feldstärketensor dessen Komponenten man auch aus denen von Fαβ erhalten kann, indem man die Vektoren
Maxwellgleichungen unter Berücksichtigung hypothetischer, magnetischer MonopoleMagnetische Monopole treten in einigen GU-Theorien als mögliche oder notwendige Bestandteile auf. Mit ihnen ließe sich die Quantelung der elektrischen Ladung erklären, wie Paul Dirac schon 1931 erkannte. Bislang ist allerdings kein magnetischer Monopol beobachtet worden. Daher wird in den oben genannten Maxwellgleichungen auch angenommen, dass keine magnetischen Monopole (magnetische Ladungen) existieren. Sollten in der Zukunft dennoch solche magnetischen Ladungen gefunden werden, so lassen sich diese in den Maxwellgleichungen problemlos berücksichtigen. Setzt man ρm für die Monopolladungsdichte, Interpretation: Die Feldlinien der magnetischen Flussdichte beginnen und enden in einer magnetischen Ladung. Interpretation: Sich zeitlich ändernde magnetische Flussdichten oder das Vorhandensein von magnetischen Stromdichten führen zu elektrischen Wirbelfeldern. Die anderen beiden Gleichungen bleiben unverändert, während sich aber natürlich für die beiden neuen differentiellen (d. h. lokalen) Gleichungen auch neue integrale (d. h. globalen) Darstellungen ergeben, die aber ohne weiteres mit den Integralsätzen von Gauß und Stokes berechnet werden können. Der Fall der verschwindenden Monopole ρm = 0 führt wieder auf die bekannten, oben angegebenen Gleichungen zurück. Maxwellsche Gleichungen unter Berücksichtigung einer hypothetischen PhotonenruhemasseDie Ruhemasse von Photonen ist 0. Als akademische Übung lassen sich die Maxwellschen Gleichungen unter Berücksichtigung einer winzigen von 0 verschiedenen Photonenruhemasse formulieren. Diese heißen dann Maxwell-Proca-Gleichungen. Gemäß Proca (1930, 1946) lässt sich dieser Fall mit einer modifizierten Lagrange-Funktion beschreiben. Die Potentiale bekommen durch die Photonenruhemasse eine besondere Bedeutung: Beispielsweise wird das statische elektrische Potential einer Punktladung zu einem sphärisch symmetrischen Yukawa-Potential. Damit wird die Reichweite der elektrischen Kräfte (Kraftübertragung durch Photonen) massiv eingeschränkt. Literatur
|
|||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Maxwellsche_Gleichungen aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





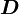 -Feld ist ein Quellenfeld. Die Ladung (
-Feld ist ein Quellenfeld. Die Ladung (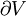 eines Volumens V ist gleich der elektrischen Ladung in seinem Inneren.
eines Volumens V ist gleich der elektrischen Ladung in seinem Inneren.
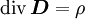
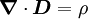
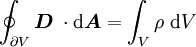
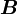 -Feld ist quellenfrei. Es gibt keine
-Feld ist quellenfrei. Es gibt keine 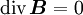
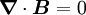
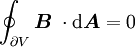
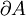 einer Fläche A ist gleich der negativen zeitlichen Änderung des magnetischen Flusses durch die Fläche.
einer Fläche A ist gleich der negativen zeitlichen Änderung des magnetischen Flusses durch die Fläche.
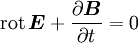
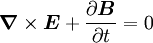
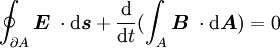
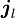 und von der elektrischen Flussdichte
und von der elektrischen Flussdichte 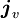 bezeichnet und ergibt als Summe mit der Leitungsstromdichte die totale Stromdichte
bezeichnet und ergibt als Summe mit der Leitungsstromdichte die totale Stromdichte 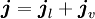 :
:
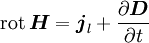
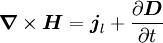
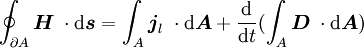
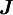 als wesentlicher Bestandteil des
als wesentlicher Bestandteil des 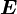 verknüpft.
verknüpft.
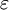 mit der
mit der 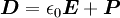 , mit der elektrischen Polarisation
, mit der elektrischen Polarisation 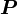 , dem elektrischen Dipolmoment pro Volumen.
, dem elektrischen Dipolmoment pro Volumen.
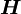 verknüpft. Noch allgemeiner gilt
verknüpft. Noch allgemeiner gilt 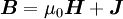 , mit der magnetischen Polarisation
, mit der magnetischen Polarisation 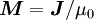 bezeichnet).
bezeichnet).
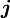 verwechselt werden.
verwechselt werden.
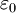 bzw.
bzw. 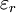 und
und 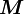 werden dort gleich bezeichnet, als cgs-Magnetisierung, und unterscheiden sich nur um einen Faktor
werden dort gleich bezeichnet, als cgs-Magnetisierung, und unterscheiden sich nur um einen Faktor 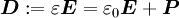
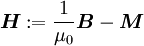 oder
oder
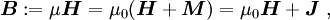
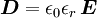 und
und 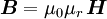 .
.
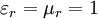 wird.
wird.
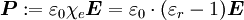 , mit
, mit 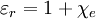
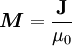 gilt entsprechend, mit der
gilt entsprechend, mit der 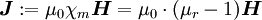 , mit
, mit 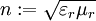 und der Lichtgeschwindigkeit im Vakuum
und der Lichtgeschwindigkeit im Vakuum 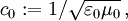
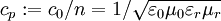 ,
,
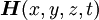 . In den partiellen Differantialgleichungen tritt dann neben den Ortsvariablen auch die Zeitvariable auf. Zur vereinfachten Lösung dieser Differentalgleichungen beschränkt man sich in Praxis oft auf harmonische (sinusförmige) Vorgänge. Diese Darstellung ist für die praktische Feldberechnung, beispielsweise bei der Berechnung von elektromagnetischen Schirmen oder für die
. In den partiellen Differantialgleichungen tritt dann neben den Ortsvariablen auch die Zeitvariable auf. Zur vereinfachten Lösung dieser Differentalgleichungen beschränkt man sich in Praxis oft auf harmonische (sinusförmige) Vorgänge. Diese Darstellung ist für die praktische Feldberechnung, beispielsweise bei der Berechnung von elektromagnetischen Schirmen oder für die 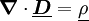
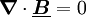
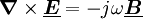
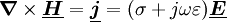
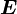 ,
, 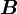 usw. durch Größen ausdrücken, die ein klar definiertes, einfaches Transformationsverhalten unter Lorentz-Transformationen haben, also durch Lorentz-Skalare, Vierervektoren und Vierer-Tensoren höherer Stufen.
usw. durch Größen ausdrücken, die ein klar definiertes, einfaches Transformationsverhalten unter Lorentz-Transformationen haben, also durch Lorentz-Skalare, Vierervektoren und Vierer-Tensoren höherer Stufen.
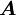 (
(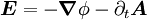

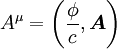
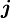 die Viererstromdichte zusammensetzen, mit
die Viererstromdichte zusammensetzen, mit
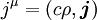 .
.
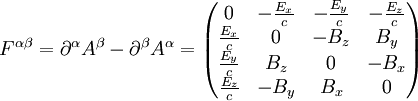 .
.
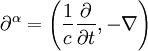 , also
, also 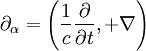 , sowie die Differentiale
, sowie die Differentiale 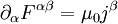
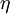 = diag(+1,-1,-1,-1) .
= diag(+1,-1,-1,-1) .
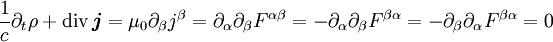 .
.
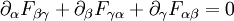
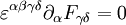
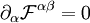
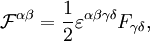
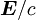 durch
durch 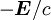 ersetzt. Also
ersetzt. Also
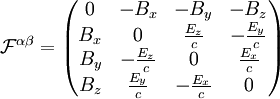 .
.
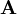 und
und 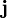 dargestellt, der Feldstärketensor durch die 2-Form
dargestellt, der Feldstärketensor durch die 2-Form 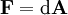 und sein Dual durch die 2-Form
und sein Dual durch die 2-Form 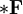 (das Symbol
(das Symbol 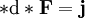 und
und 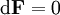 .
.
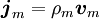 für die Stromdichte und
für die Stromdichte und 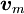 für die Geschwindigkeit der sich bewegenden magnetischen Monopolladungen, so ändern sich nur zwei der vier oben genannten Gleichungen in differentieller Form zu
für die Geschwindigkeit der sich bewegenden magnetischen Monopolladungen, so ändern sich nur zwei der vier oben genannten Gleichungen in differentieller Form zu