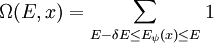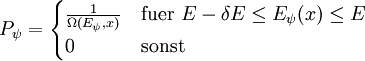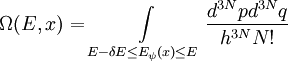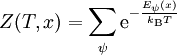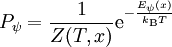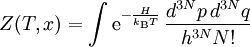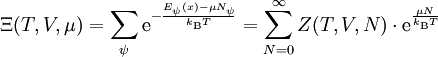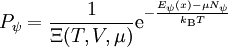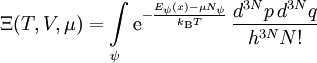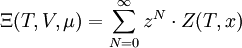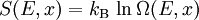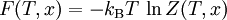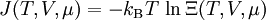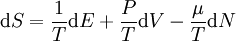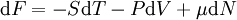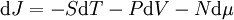Meine Merkliste
my.chemie.de  

my.chemie.de

Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.

  • Meine Merkliste
  • Meine gespeicherte Suche
  • Meine gespeicherten Themen
  • Meine Newsletter
Jetzt kostenlos registrieren
Login  
ger  
DeutschEnglishFrançaisEspañol

Zustandssumme



Zustandssummen sind wesentliche Werkzeuge der statistischen Physik. Aus einer Zustandssumme (der Funktion, nicht dem Wert) lassen sich alle thermodynamischen Größen ableiten. Wenn die Teilchenzahlen N groß genug sind, kann man das System auch als kontinuierlich ansehen und die Zustandssummen als Zustandsintegrale formulieren.

Inhaltsverzeichnis

Mikrokanonische Zustandssumme

Die mikrokanonische Zustandssumme Ω(E,x) ist die Zahl der erreichbaren Mikrozustände ψ eines abgeschlossenen Systems im Gleichgewicht bei fester Gesamtenergie E und festen äußeren Parametern x.

Der Γ-Raum (auch Phasenraum genannt) eines idealen Gases hat 6N Dimensionen - 3N Dimensionen für die Ortskoordinaten und 3N für die Impulskoordinaten der N Teilchen. Die in der Mikrokanonik betrachteten abgeschlossenen Systeme haben eine konstante Energie, die im Γ-Raum als Fläche erscheint, auf der sich das System bewegen kann. Summiert bzw. integriert wird dabei über die Energieschale von E − δE bis E auf der Hyperfläche des Systems im Γ-Raum. Die Schale hat dabei die Breite δE. Man summiert nur über den Rand der Energiesphäre, da sich für N > > 1 fast alle Zustände auf dem Rand befinden.

\Omega (E,x) = \sum_{ E - \delta E \le E_{\psi} (x) \le E } 1

Die Wahrscheinlichkeit, einen bestimmten Mikrozustand ψ anzutreffen, ist:

P_\psi = \begin{cases} \frac{1}{\Omega(E_\psi, x)} & \mbox{fuer } E - \delta E \le E_\psi(x) \le E \\ 0 & \mbox{sonst} \end{cases}


In integraler Schreibweise wird die Zustandssumme zum Zustandsintegral:

\Omega(E,x) = \int\limits_{E - \delta E \le E_\psi(x) \le E} \frac{d^{3N} p d^{3N} q}{h^{3N} N!}

Kanonische Zustandssumme

Bei der kanonischen Zustandssumme wird nicht die Energie des Systems vorgegeben, sondern die Temperatur. Das zugehörige Ensemble heißt kanonisches Ensemble oder Gibbs-Ensemble. Für die Zustandssumme ergibt sich dann folgende Beziehung:

Z(T,x) = \sum_\psi\mathrm{e}^{-\frac{E_\psi(x)}{k_\mathrm{B}T}}

Die Wahrscheinlichkeit, einen bestimmten Mikrozustand ψ anzutreffen, ist:

P_\psi = \frac{1}{Z(T,x)} \mathrm{e}^{-\frac{E_\psi(x)}{k_\mathrm{B} T}}

Das kanonische Zustandsintegral ist:

Z(T,x) = \int \mathrm{e}^{-\frac{H}{k_\mathrm{B}T}} \, \frac{d^{3N} p \, d^{3N} q}{h^{3N} N!}

H ist in diesem Fall die Hamilton-Funktion.
Der Faktor 1/N! stammt von der Tatsache, dass die Teilchen nicht unterscheidbar sind. Wenn man diesen Faktor wegließe, würde man N!-mal zuviele Mikrozustände des Systems zählen.

Großkanonische Zustandssumme

Die großkanonische Zustandssumme stellt eine Erweiterung der kanonischen Zustandssumme dar. Hier wird neben der Temperatur auch das chemische Potential μ vorgegeben.

\Xi(T, V, \mu) = \sum_\psi\mathrm{e}^{-\frac{E_\psi(x) - \mu N_\psi}{k_\mathrm{B}T}} = \sum_{N=0}^\infty Z(T,V,N)\cdot\mathrm{e}^{\frac{\mu N}{k_\mathrm{B}T}}

Die Wahrscheinlichkeit, einen bestimmten Mikrozustand ψ anzutreffen, ist:

P_\psi = \frac{1}{\Xi(T, V, \mu)} \mathrm{e}^{-\frac{E_\psi(x) - \mu N_\psi}{k_\mathrm{B} T}}

In integraler Schreibweise lautet die Zustandssumme, bzw. das Zustandsintegral:

\Xi(T, V, \mu) = \int\limits_{\psi} \mathrm{e}^{-\frac{E_\psi(x) - \mu N_\psi}{k_\mathrm{B}T}} \, \frac{d^{3N} p \, d^{3N} q}{h^{3N} N!}

Es gibt einen eleganteren Weg, von der kanonischen Zustandssumme zur großkanonischen zu kommen: Man nimmt die kanonische Zustandssumme und summiert sie zusammen mit der Fugazität auf:

\Xi(T, V, \mu) = \sum\limits_{N=0}^{\infty} z^N \cdot Z(T,x)

z ist dabei die Fugazität.

Thermodynamische Potentiale

S(E, x) = k_\mathrm{B} \,\ln\Omega(E,x)
F(T, x) = - k_\mathrm{B}T \,\ln Z(T, x)
J(T, V, \mu) = - k_\mathrm{B}T \,\ln \Xi(T, V, \mu)

Hier ist S die Entropie, F ist die Helmholtz-Energie (auch freie Energie genannt), sowie J das Großkanonische Potential.

Für x = V (das Volumen), ergeben sich folgende totale Differentiale, wobei P der Druck ist:

\mathrm{d}S = \frac{1}{T} \mathrm{d}E + \frac{P}{T} \mathrm{d}V - \frac{\mu}{T} \mathrm{d}N
\mathrm{d}F = - S \mathrm{d}T - P \mathrm{d}V + \mu \mathrm{d}N \,
\mathrm{d}J = - S \mathrm{d}T - P \mathrm{d}V - N \mathrm{d} \mu \,

Hinweis

Die Englische Übersetzung von Zustandssumme ist partition function.

Partition bedeutet hier Zustand: Die Darstellung einer Zahl in allen ihren Zuständen als Summe positiver Ganzzahlen, z. B. sind die Zustände von 4:

  • 1+1+1+1
  • 1+1+2
  • 1+3
  • 2+2
  • 4

Die Quantenmechanik und statistische Physik ordnet auf diese Weise Atome in Zellen an.

Zu der mathematischen Seite siehe den Artikel Partitionsfunktion.

Siehe auch

Literatur

  • Torsten Fließbach: Statistische Physik (1995), ISBN 3860257153 - Eine Einführung in die Statistische Physik und Thermodynamik
 
Dieser Artikel basiert auf dem Artikel Zustandssumme aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar.
Ihr Bowser ist nicht aktuell. Microsoft Internet Explorer 6.0 unterstützt einige Funktionen auf ie.DE nicht.