Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
RatengleichungRatengleichungen beschreiben die zeitlichen Konzentrationsverläufe verschiedener Spezies, zum Beispiel bei gekoppelten chemischen Reaktionen, oder bei An- und Abregungsprozessen verschiedener Niveaus bei Atomen oder Molekülen:
Bei den Ratengleichungen handelt es sich i.a. um ein System von gekoppelten, steifen, nichtlinearen Differentialgleichungen erster Ordnung, für die die Bausteinerhaltung gelten muss. Im stationären Fall Produkt-Highlight
RatenkoeffizentenDie in den Ratengleichungen auftretenden Reaktionsratenkoeffizienten können allgemein als beliebige Funktionen der jeweiligen, gegebenenfalls zeitabhängigen Temperatur (siehe auch Plasmaphysik: Thermisches Gleichgewicht) betrachtet werden. Im allgemeinen müssen Ratenkoeffizienten für chemische Prozesse der schweren Teilchen aus der Literatur entnommen werden ('Geschwindigkeitskonstante' einer chemischen Reaktion), die Ratenkoeffizienten für die elektronenstoßinduzierten Prozesse können mit Hilfe der Elektronenkinetik erhalten werden. Grundlage für die kinetische Behandlung der Elektronen, sowohl zur Berechnung derartiger Ratenkoeffizienten, als auch elektronischer Transportprozesse (elektrische Leitfähigkeit) bildet die Boltzmann-Gleichung für die Elektronenenergieverteilung. BeispielZur Verdeutlichung wird die Wasserstoffoxidation herangezogen:
ein Teil dissoziiert
Die Ratengleichungen (Gl.1) für die sechs Spezies lauten:
Numerische LösungsmethodenDa es sich bei den Ratengleichungen um ein System von steifen Differentialgleichungen handelt, ist man gezwungen ein Verfahren mit einem möglichst großen Stabilitätsgebiet zu wählen, damit die Integrationsschritte nicht allzu klein werden. Am günstigsten sind A-stabile Verfahren. Für die Ratengleichungen bedeutet 'steif', dass sich die Zeitkonstanten der verschiedenen Spezies sehr stark unterscheiden: Im Verhältnis zu anderen ändern sich einige Konzentrationen nur sehr langsam. Zwei Beispiele absolut steif-stabiler Integrationsverfahren sind die Implizite Trapez-Methode und die Implizite Euler-Methode. Zur Lösung von Ratengleichungen sind auch einige BDF-Verfahren (backward differentiation formula), z.B. nach Gear und Hindmarsh, geeignet. BausteinerhaltungDas Prinzip der Bausteinerhaltung liefert eine Möglichkeit, die Güte der numerischen Lösungen zu überprüfen, denn es gilt zu jedem Zeitpunkt: wobei
HerleitungEine Spezies i, hier geschrieben als Ai setzt sich dabei aus den Bausteinen Bk folgendermaßen zusammen:
in die Ratengleichung (Gl.1) eingesetzt und über alle Spezies summiert, liefert wegen Beispiel für die Matrix βik
Literatur
|
|||||||
| Dieser Artikel basiert auf dem Artikel Ratengleichung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


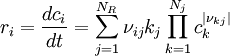
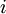 die an den Reaktionen beteiligten Spezies.
die an den Reaktionen beteiligten Spezies.
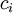 Konzentration der Spezies
Konzentration der Spezies 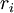 Reaktionsgeschwindigkeit der Spezies
Reaktionsgeschwindigkeit der Spezies 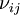 sind die
sind die 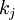 Ratenkoeffizienten (i.A.
Ratenkoeffizienten (i.A. 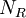 Anzahl der Reaktionen,
Anzahl der Reaktionen,
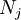 die j Produkte werden über die Konzentrationen mit negativen
die j Produkte werden über die Konzentrationen mit negativen 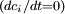 liefert Gleichung 1 das
liefert Gleichung 1 das 


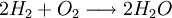
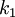 )
)
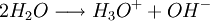
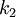 )
)
![\frac{d}{dt}[H_2] = -2 k_1 [H_2]^2 [O_2]](images/math/d/3/4/d34c4cd605251cea1670933875221cab.png)
![\frac{d}{dt}[O_2] = -k_1 [H_2]^2 [O_2]](images/math/4/1/1/41185163cf4714ba66b1da3c9c2cc6a6.png)
![\frac{d}{dt}[H_2 O] = +2k_1 [H_2]^2 [O_2] - 2k_2[H_2 O]^2](images/math/f/f/b/ffbbb54e81f8eb32ae27a19a98097f58.png)
![\frac{d}{dt}[H_3 O^+] = +k_2[H_2 O]^2](images/math/6/e/4/6e427c5b72ed73f41cd3b95183632b37.png)
![\frac{d}{dt}[OH^-] = +k_2[H_2 O]^2](images/math/8/c/c/8cc7207b205662a3ea9fbd055e3fd87a.png)
![c_1 \equiv [H_2], \;\; c_2 \equiv [O_2], \;\; c_3 \equiv [H_2 O], \;\; c_4 \equiv [H_3 O^+], \;\; c_5 \equiv [OH^-]](images/math/6/3/9/6390694eba79d4d061dd637662b3e806.png)
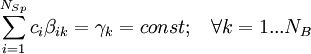
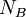 Minimale Anzahl der Bausteine,
Minimale Anzahl der Bausteine,
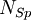 Anzahl an den Reaktionen beteiligten Spezies.
Anzahl an den Reaktionen beteiligten Spezies.
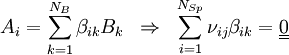 .
.
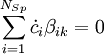 die oben genannte Bausteinerhaltung.
die oben genannte Bausteinerhaltung.