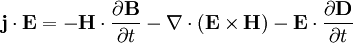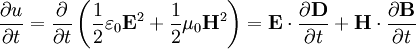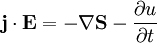Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Satz von PoyntingDer Satz von Poynting stellt einen Erhaltungssatz in der Elektrodynamik dar. Damit wird der Energieerhaltungssatz auf elektromagnetische Felder verallgemeinert. Seine Formulierung wird dem britischen Physiker John Henry Poynting zugeschrieben. Stark vereinfacht trägt er in sich die Aussage, dass ein elektromagnetisches Feld Arbeit verrichten kann, wenn es dabei „schwächer“ wird. Mathematisch kann er, wie auch die Maxwellschen Gleichungen, sowohl in einer differenziellen als auch in einer integralen Schreibweise angegeben werden. In seiner integralen Form lautet er: Produkt-HighlightWobei:
Er besagt, dass die Leistung eines Feldes gleich dem Austritt des Energiestromes und der Abnahme der Feldenergie ist. Damit ist er vergleichbar mit dem Energieerhaltungssatz. Das kann man sich klar machen, wenn man den Gaußschen Satz in der Integralform anwendet: Das Oberflächenintegral entspricht dann dem Fluss der Leistungsdichte durch die betrachtete Oberfläche. Mit diesem Satz wird gleichzeitig die Definition des Poynting-Vektors ersichtlich. Da nur seine Divergenz hier relevant ist, könnte prinzipiell auch eine Rotation einer beliebigen Funktion zu ihm hinzugefügt werden, da sie unter der Einwirkung der Divergenz verschwindet. HerleitungAusgangspunkt ist die Arbeit, die ein elektromagnetisches Feld an einer Ladung pro Sekunde verrichtet: Es bleibt anzumerken, dass der magnetische Teil des Feldes keine Arbeit verrichet, da die Lorentzkraft senkrecht zu Bewegungsrichtung der Ladung wirkt. Nun gilt aber das Durchflutungsgesetz: führt. Zieht man daneben noch die Rechenregel für die Divergenz heran, so ergibt sich
Die Rotation des elektrischen Feldes kann schließlich über das Induktionsgesetz ankämen. Hier bleibt es nur noch mit Hilfe der Definition des Poynting-Vektors und der Energiedichte die Gleichung zusammenzufassen, wozu noch die folgenden Identitäten benötigt werden: und Womit schließlich die differenzielle Form das Satzes gerechtfertigt wäre. Literatur
|
| Dieser Artikel basiert auf dem Artikel Satz_von_Poynting aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


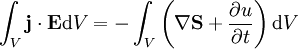



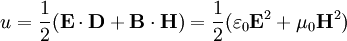 elektromagnetische Energiedichte der Felder im Vakuum.
elektromagnetische Energiedichte der Felder im Vakuum.
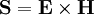
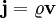
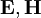
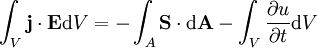
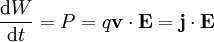
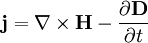 . Was oben eingesetzt auf
. Was oben eingesetzt auf
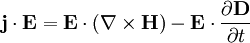

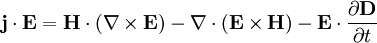 .
.
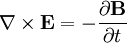 ausgedrückt werden, womit wir bei
ausgedrückt werden, womit wir bei