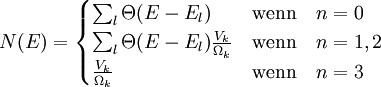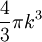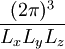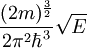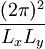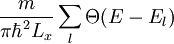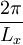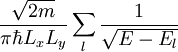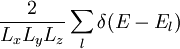Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
ZustandsdichteDie Zustandsdichte D(E) bzw. D(ω) ist eine physikalische Größe der Festkörperphysik, die angibt, wie viele Zustände innerhalb des Energie- bzw. Frequenzintervalls [E,E + dE] bzw. [ω,ω + dω] existieren. Produkt-HighlightIm 3-dim. Die Zustandsdichte kann sich auf verschiedene Objekte beziehen wie z.B. auf Phononen, Elektronen, Magnonen, Quasiteilchen in Supraleitern und vieles mehr. Die Zustandsdichte für ein n-dimensionales ElektronengasIn einem n-dimensionalen Elektronengas können sich Ladungsträger in den Dimensionen 1,..,n frei bewegen. Der entsprechende Anteil der Energie ist kontinuierlich und kann unter Nutzung der parabolischen Näherung in Abhängigkeit vom Betrag des Wellenvektors angegeben werden: Dabei ist m die effektive Masse des Ladungsträgers im Festkörper. Im Gegensatz dazu ist die Energiekomponente der anderen Dimensionen diskretisiert in den Werten El. Die Zustandsdichte kann allgemein beschrieben werden:
Der Vorfaktor 2 entspricht den zwei möglichen Spinzuständen. V ist das Halbleitervolumen. N(E) steht für die Anzahl aller bei der Energie E zugänglichen Zustände: Im n-dimensionalen k-Raum beschreibt Vk das Gesamtvolumen aller Zustände, die bei der verbleibenden Energie E − El zugänglich sind; Ωk ist das Volumen eines solchen Zustandes. In der folgenden Tabelle sind die Werte für verschieden dimensionale Elektronengase angegeben:
Die Zustandsdichte im HalbleiterIn Halbleitermaterialien wird wegen der periodisch auftretenden Atomkernen ein ähnlicher Ansatz für das Leitungs- und Valenzband gemacht (siehe Bändermodell). Den frei beweglichen Ladungsträgern in den beiden Bändern, also Elektronen und Löchern, wird eine effektive Masse zugewiesen und die Zustandsdichten für die beiden Bänder wie oben als quadratisch angenommen. Den Abstand der Extrema dieser beiden Zustandsdichten bezeichnet man als Bandlücke. Dabei wird bei einer Versetzung der Extrema im k-Raum (Impulsraum) von einem indirekten, bei gleichem Impulsunterschied von einem direkten Halbleiter gesprochen.
Die Elektronen und Löcher versuchen, in diesen möglichen Zuständen ein Minimum der Energie einzunehmen und streben zur Bandkante hin, also zu den Extrema. Es treten also, soweit möglich, tatsächlich besetzte Zustände vermehrt dort auf. Bei dotierten Halbleitern treten zu diesen möglichen Zuständen noch Zustände in der Bandlücke auf. Diese sind bei n-Dotierung nahe am Leitungsband und bei p-Dotierung nahe am Valenzband. Durch Zuführen von Energie kann die Aktivierungsenergie überwunden werden und es bilden sich vermehrt besetzte Zustände in Leitungs- bzw. Valenzband. Darüber hinaus ändert sich durch Dotierung die Lage des Ferminiveaus: es wird bei n-Dotierung angehoben, bzw. senkt sich bei p-Dotierung zum Valenzband hin ab. Bei einer n-Dotierung sind damit bereits bei Raumtemperatur wegen der thermischen Energie weit mehr Zustände im Leitungsband besetzt als bei einem undotierten Material. Die zusätzlichen freien Ladungsträger können damit den Stromtransport erhöhen. Externer Link
|
||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Zustandsdichte aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





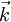 -Raum ist die Zustandsdichte
-Raum ist die Zustandsdichte 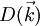 konstant gleich
konstant gleich 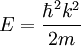
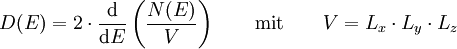 .
.