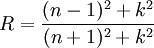Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Permittivität
Die Permittivität ε (v. lat.: permittere = erlauben, überlassen, durchlassen), auch dielektrische Leitfähigkeit genannt, gibt die Durchlässigkeit eines Materials für elektrische Felder an. Auch dem Vakuum ist eine Permittivität zugewiesen, da sich im Vakuum auch elektrische Felder einstellen oder elektromagnetische Felder ausbreiten können. Die Permittivität ist das Produkt aus der Permittivität des Vakuums ε0 und der relativen Permittivität εr:
Darin dient die relative Permittivität der Quantifizierung (meist) feldschwächender Überlagerungseffekte elektrischer Felder innerhalb elektrisch isolierender Materialien. Die Bezeichnung Dielektrizitätskonstante für Permittivität gilt als veraltet und sollte nicht mehr verwendet werden. Weiteres empfehlenswertes Fachwissen
Erläuterung der Permittivität am Beispiel isolierender StoffeAls Permittivität bezeichnet man eine Materialeigenschaft elektrisch isolierender, polarer oder unpolarer Stoffe, die auch Dielektrika genannt werden. Diese Eigenschaft äußert sich bei der Beaufschlagung der Stoffe mit elektrischen Feldern, wie zum Beispiel in einem Kondensator. Beim Anlegen eines elektrischen Feldes an einen mit Material gefüllten Kondensator orientieren sich die Ladungsträger des Isolationsmaterials am elektrischen Feldvektor und bilden ein Polarisationsfeld, das dem äußeren Feld entgegenwirkt und dieses schwächt. Dieses Phänomen der Feldschwächung lässt sich bei Annahme eines gegebenen elektrischen Erregungsfeldes dadurch beschreiben, dass dem isolierenden Material ein Faktor εr zur elektrischen Feldkonstante ε0 (Permittivität des Vakuums) zugewiesen wird. Aus der äußeren elektrischen Erregung D, auch als elektrische Flussdichte bezeichnet, ergibt sich das elektrische Feld E mit der Permittivität ε zu: Man sieht, dass bei gleicher elektrischer Erregung D und steigenden Werten von εr die elektrische Feldstärke E abnimmt. Auf diese Weise wird der feldschwächende Effekt bei gleicher elektrischer Erregung erfasst, d. h. bei vorgegebener elektrischer Flußdichte oder vorgegebener elektrischer Ladung. Unter der Einwirkung einer an den Kondensatorplatten angelegten fixen Spannung U und dem elektrischen Feld E=U/d (Plattenabstand d) ergibt sich die elektrische Erregung D mit der Permittivität ε zu: In der Elektrodynamik und auch in der Elektrostatik wird die Permittivität zur Beschreibung der o. a. Phänomene als Proportionalitätsfaktor im Zusammenhang zwischen elektrischer Erregung und elektrischer Feldstärke verwendet In Materie stellt diese Gleichung nur die niedrigste Ordnung eines im allgemeinen nichtlinearen Zusammenhangs dar: Im Falle großer Feldstärken fasst man entweder die Permittivität als feldstärkeabhängig auf und schreibt ε(E), oder man führt neben ε=ε(1) weitere Taylor-Koeffizienten ein, ε(2) usw., die die Feldstärkeabhängigkeit von D beschreibt: Im Vakuum als Referenzmaterial eines Isolierstoffes gilt die relative Permittivität Permittivität des VakuumsDie Permittivität des Vakuums ε0 wird nach dem derzeitigen deutschsprachigen Entwurf des Internationalen Größensystems als elektrische Feldkonstante bezeichnet. Weitere Bezeichnungen sind:
Im Vakuum besteht zwischen der magnetischen Feldkonstante μ0, der elektrischen Feldkonstante ε0 und der Vakuumlichtgeschwindigkeit c0 der folgende von Maxwell vorhergesagte und 1857 von Wilhelm Eduard Weber und Rudolf Kohlrausch experimentell bestätigte Zusammenhang:
Mit den (durch Definition) exakt bekannten Naturkonstanten Neben dem Coulomb-Gesetz, dem ampèreschen Gesetz und dem faradayschen Induktionsgesetz stellt dieser Zusammenhang eine weitere Verknüpfung elektromagnetischer und mechanischer Einheiten dar, die bei der Wahl eines elektromagnetischen Einheitensystems zu berücksichtigen ist. In Einheitensystemen, die die elektromagnetischen Größen explizit auf mechanische Basisgrößen zurückführen, namentlich den verschiedenen Varianten des CGS-Einheitensystems, wird ε0 als dimensionslose Zahl gewählt: (Heaviside-Lorentz-Einheitensystem), (elektrostatisches, elektromagnetisches oder gaußsches Einheitensystem; in diesen System kürzt sich das 4π aus dem Coulomb-Gesetz heraus). Im SI-System geschieht die Rückführung der elektromagnetischen auf die mechanischen Größen in der Definition der Stromstärke (Ampere), die darauf hinausläuft, dass die magnetische Permeabilität des Vakuums als definiert wird, woraus folgt Relative PermittivitätNeben der Bezeichnung relative Permittivität für εr sind noch folgende Bezeichnungen gebräuchlich:
Nur für isotrope Medien bei konstanter Temperatur und konstanter Frequenz des elektrischen Feldes ist εr eine statische, skalare Größe. In diesem einfachsten Fall gibt sie den Faktor an, um den die Spannung an einem Kondensator sinkt, wenn man zwischen den Kondensatorplatten nicht nur Vakuum (oder mit wenig Fehler auch einfach Luft), sondern ein dielektrisches, nicht leitendes Material anordnet. Relative Permittivität in kristallinen StrukturenIm allgemeinen ist εr jedoch ein Tensor zweiter Stufe, der die kristalline (oder anders geordnete) Struktur der Materie widerspiegelt und damit die Richtungsabhängigkeit der Faktoren. Die Tensoreigenschaft der Permittivität ist Grundlage für die Kristalloptik. Die relative Permittivität εr ist ein Tensor zweiter Stufe (und damit als Funktion der Lichtausbreitungsrichtung relativ zu ausgezeichneten Kristallachsen), der sowohl von der Frequenz (also bei Betrachtung von Licht von dessen Wellenlänge) als auch vom äußeren elektrischen Feld und magnetischen Feldern abhängig ist, und wird auch dielektrische Funktion genannt. Vor allem im Englischen wird auch das Größensymbol κ verwendet (siehe Low-k-Dielektrikum bzw. High-k-Dielektrikum). Frequenzabhängigkeit der relativen PermittivitätDie Permittivität in Materie ist frequenzabhängig und kann beispielsweise über das einfache Modell des Lorentz-Oszillators recht gut modelliert werden. Diese Frequenzabhängigkeit wird Dispersion genannt. In Tabellenwerken angegeben ist in der Regel der Zahlenwert bei niedrigen Frequenzen (Größenordnung Hz–kHz, je nach Messmethode allenfalls MHz), bei denen die molekularen Dipole (und a forteriori die atomaren Elektronenorbitale) dem äußeren Feld folgen können. Das Zurückbleiben der Moleküle gegenüber dem hochfrequenten elektrischen Feld wird makroskopisch mit einer komplexen relativen Permittivität beschrieben. Komplexwertige relative PermittivitätDie relative Permittivität εr ist allgemein komplexwertig. Genauso wie bei Gleichfeldern bilden sich auch bei Wechselfeldern in Dielektrika Polarisationsfelder, die aber gegebenenfalls der angelegten äußeren Feldgröße um einen gewissen Phasenwinkel nacheilen. Dabei bleibt die Orientierung der Ladungsträger im Dielektrikum in der Phase (zeitlich) hinter der Umpolarisierung des angelegten Wechselfeldes zurück. Mit zunehmender Frequenz wird dieser Effekt stärker. Es lässt sich leicht vorstellen, dass Wechselfelder hoher Frequenz durch schnelles, wiederkehrendes Umpolarisieren in isolierenden Materialien Wärmeverluste erzeugen. Bei noch höheren Frequenzen, mit denen Ladungsträger im Bändermodell eines Kristalls angeregt werden können, wird ebenfalls Energie absorbiert. Diesen Phänomenen wird dadurch Rechnung getragen, dass die relative Permittivität komplexwertig mit: beschrieben wird, wobei die dielektrischen Verluste über den Imaginärteil der Permittivität erfasst werden. Eine weitverbreitete Anwendung, die das Phänomen dielektrischer Verluste ausnutzt, ist der Mikrowellenofen. Die Verlustleistungsdichte bei dielektrischer Erwärmung beträgt, bezogen auf das Materialvolumen: Die mit der Verlustleistung verbundene dielektrische Erwärmung entspricht bei Integration über den Erwärmungszeitraum exakt der einem Materialvolumen mit elektromagnetischen Wellen zugeführten inneren Energie eines Materials, wie in der Thermodynamik beschrieben. Der Imaginärteil der komplexwertigen, relativen Permittivität ist ein Maß für Fähigkeit eines Stoffes, elektromagnetische Feldenergie bei Hochfrequenz in Wärmeenergie zu wandeln. TemperaturabhängigkeitTemperaturabhängig ist beispielsweise die komplexwertige relative Permittivität von Wasser, deren Realteil bei Raumtemperatur einen Wert von etwa achtzig annimmt, und bei 95 °C circa fünfundfünfzig beträgt. Die Abnahme der Permittivität bei steigender Temperatur hängt mit dem Grad der Unordnung der Ladungsträger bei einer Zunahme der inneren Energie zusammen. Molekular betrachtet nimmt die Polarisierbarkeit aufgrund der zunehmenden Eigenbewegung der Ladungsträger bei höherer innerer Energie ab; makroskopisch betrachtet sinkt somit die relative Permittivität bei Temperaturerhöhung. Relative Permittivität ausgewählter Materialien
Tabellierte, umfassende Übersichten frequenz- und temperaturabhängiger, komplexer relativer Permittivitäten vieler Materialien finden sich in [1] und vor allem in [2] Verallgemeinerungen zur Dispersion, Richtungsabhängigkeit und MagnetfeldAus den Maxwell-Gleichungen folgt ein Zusammenhang zwischen der Brechzahl, der elektrischen Permittivität und der magnetischen Permeabilität, Hier sind ε und μ bei der einschlägigen optischen Frequenz (größenordnungsmäßig im Bereich 1015 Hz) gemeint. Für gasförmige, flüssige und feste Materie ist εr größer eins. Allerdings gibt es in anderen Materiezuständen, z. B. im Plasma (sog. „vierter Aggregatzustand“), auch Werte, die kleiner als eins sein können. In dispersiven Materialien hat man es mit der Reaktion des Materials auf elektromagnetische Felder mit der Frequenz von Licht zu tun, also sehr hohen Frequenzen über einen weiten Frequenzbereich. Hier muss der Zusammenhang zwischen der Brechzahl und den bei niedrigen Frequenzen gemessenen ε wesentlich allgemeiner gefasst und die Frequenzabhängigkeit berücksichtigen werden (siehe Lorentz-Oszillator). Auf diese Weise können Absorptions- und Reflexionsspektren von Materialien gut dargestellt werden. Die Dielektrizitätskonstante wird dabei als komplexe Größe verwendet, mit einem Realteil ε1 (auch ε’ oder εr, nicht zu verwechseln mit r für relativ) und einem Imaginärteil ε2 (auch ε’’ oder εi). Dabei können in diesen beiden Komponenten direkt die Beiträge verschiedener Mechanismen im Material (z. B. Bandübergänge) angegeben und in ihrer Frequenzabhängigkeit addiert werden – eine detailliertere Darstellung findet sich unter elektrische Suszeptibilität. Über die Kramers-Kronig-Relation kann dann der (dispergierende) Zusammenhang zwischen der komplexen Dielektrizitätskonstanten und den optischen Kenngrößen Brechzahl n und Absorptionskoeffizient k dargestellt werden. Dies führt zu den theoretischen Spektren von Absorption und Reflexion, die mit gemessenen Spektren vergleichen und anpassen werden können. Für die Berechnung solcher Spektren (von Reflexion oder auch Absorption) können im Fall von
umgekehrt gilt:
Ebenfalls kann u. a. der Reflexionsgrad R berechnet werden: Auf Grund ihrer Kristallstruktur sind die Eigenschaften einiger Materialien richtungsabhängig, z. B. doppelbrechenden Materialen. Diese Materialien finden u. a. Anwendung bei Verzögerungsplatten. Mathematisch lässt sich diese Eigenschaft durch Darstellung in Tensorform erfassen, mit Komponenten für die einzelnen Richtungen. Diese sind wiederum als frequenzabhängig anzusetzen und sogar je nach Richtung in verschiedenem Maße. Neben der „natürlichen“ Richtungsabhängigkeit können die Eigenschaften auch durch äußere Einwirkungen wie ein Magnetfeld (siehe Magnetooptik) oder Druck eine ähnliche Richtungsabhängigkeit bewirken. Einzelnachweise
Literatur
Kategorien: Elektrodynamik | Vakuumtechnik |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Permittivität aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


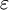
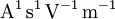



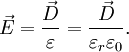
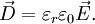
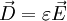
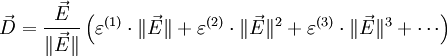
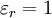
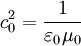 .
.
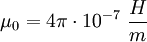 und
und 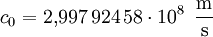 sowie der Kreiszahl Pi mit
sowie der Kreiszahl Pi mit 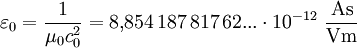
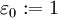
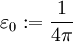
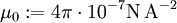
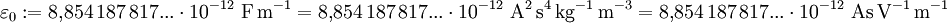
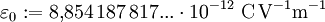
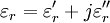
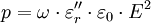
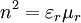
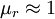 (nichtmagnetisches Material) die Größen n und k der komplexen Brechzahl direkt aus den Real- und Imaginärteilen der Permittivität bestimmt werden:
(nichtmagnetisches Material) die Größen n und k der komplexen Brechzahl direkt aus den Real- und Imaginärteilen der Permittivität bestimmt werden:
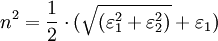 bzw.
bzw. 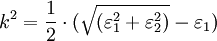
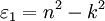 bzw.
bzw.