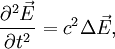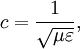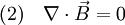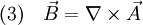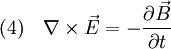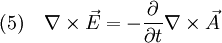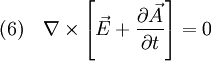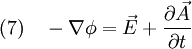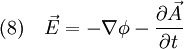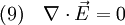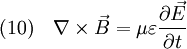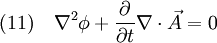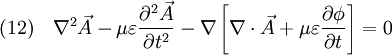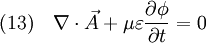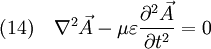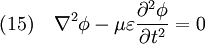Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Elektromagnetische WelleAls elektromagnetische Welle bezeichnet man eine Welle aus gekoppelten elektrischen und magnetischen Feldern. Zu ihnen gehören unter anderem Radiowellen, Mikrowellen, Infrarotstrahlung, sichtbares Licht, UV-Strahlung sowie Röntgen- und Gammastrahlung – kurz, das gesamte elektromagnetische Wellenspektrum. Der einzige Unterschied zwischen diesen Wellentypen liegt in ihrer Frequenz und somit ihrer Energie. Es gibt jedoch ein kontinuierliches Spektrum (siehe Grafik unten); die Einteilung in die oben genannten Typen beruht auf den sich mit der Frequenz kontinuierlich ändernden Eigenschaften der Strahlung oder ihrer Herkunft sowie auf den davon abhängigen unterschiedlichen Verwendungen oder Herstellungsverfahren oder den verschiedenen dafür benutzten Messmethoden. Elektromagnetische Wellen benötigen kein Medium, um sich auszubreiten. Sie pflanzen sich im Vakuum unabhängig von ihrer Frequenz mit Lichtgeschwindigkeit fort. Sie sind Transversalwellen, d. h. ihre Ausbreitungsrichtung steht senkrecht zur Schwingungsrichtung der elektromagnetischen Felder. Unter bestimmten Umständen verhalten sich elektromagnetische Wellen wie Teilchen (siehe Welle-Teilchen-Dualismus). Diese nennt man Photonen. Produkt-Highlight
EigenschaftenWellencharakterPhysikalisch betrachtet, handelt es sich bei elektromagnetischen Wellen um sich ausbreitende Schwingungen des elektromagnetischen Feldes. Hierbei stehen elektrisches und magnetisches Feld bei linear polarisierten Wellen senkrecht aufeinander und haben ein festes Größenverhältnis. Dieses ist gerade durch die Wellenimpedanz gegeben. Insbesondere verschwinden elektrisches und magnetisches Feld an denselben Orten zur selben Zeit, so dass die häufig gelesene Darstellung, dass sich elektrische und magnetische Energie zyklisch ineinander umwandeln, nicht richtig ist. Sie stimmt allerdings z. B. für das Nahfeld eines elektromagnetische Wellen erzeugenden elektrischen Dipols oder Schwingkreises. Die Entstehung elektromagnetischer Wellen erklärt sich aus den Maxwellschen Gleichungen: Die zeitliche Änderung des elektrischen Feldes ist stets mit einer räumlichen Änderung des magnetischen Feldes verknüpft. Ebenso ist wiederum die zeitliche Änderung des magnetischen Feldes mit einer räumlichen Änderung des elektrischen Feldes verknüpft. Für periodisch (insbesondere sinusförmig) wechselnde Felder ergeben diese Effekte zusammen eine fortschreitende Welle. TeilchencharakterFür bestimmte Eigenschaften elektromagnetischer Wellen (z. B. Photoelektrischer Effekt), genügt das oben beschriebene Wellenmodell nicht mehr, um alle beobachtbaren Phänomene zu beschreiben, vielmehr treten die Teilcheneigenschaften einzelner Photonen, der Quanten des elektromagnetischen Feldes, in den Vordergrund. Der Wellencharakter (etwa Interferenz) bleibt aber voll erhalten. Man spricht deshalb vom Dualismus von Teilchen und Welle. Im Rahmen dieser Teilchenvorstellung des Lichtes wird jeder Frequenz f die Energie eines einzelnen Photons Wellen im MediumIn einem Medium (also in Materie) verringert sich die Geschwindigkeit abhängig von der Permittivität (dielektrische Leitfähigkeit) und der Permeabilität (magnetische Leitfähigkeit) des Stoffes. Es gilt dann: Einige neuere Theorien, zum Beispiel die Schleifenquantengravitation, sagen eine geringe Frequenzabhängigkeit der Lichtgeschwindigkeit c im Vakuum voraus. SpektrumElektromagnetische Wellen sind im elektromagnetischen Spektrum nach der Wellenlänge sortiert (eine Liste von Frequenzen und Beispiele elektromagnetischer Wellen gibt es im dortigen Artikel). Das am besten bekannte und am meisten studierte Beispiel einer elektromagnetischen Welle ist das sichtbare Licht. Es stellt nur einen winzigen Teil des gesamten Spektrums dar und ist der einzige Bereich, der von Menschen ohne technische Hilfsmittel wahrgenommen werden kann. Rechts davon ist die Energie der Photonen zu gering, um chemische Prozesse auslösen zu können. Links davon beginnt der Bereich der ionisierenden Strahlung (Radioaktivität), bei der ein einziges Photon Moleküle zerstören kann. Beim Licht bestimmt die Frequenz die Farbe des Lichtes und nicht, wie oft fälschlicherweise angenommen, die Wellenlänge. Deutlich wird dies, wenn man Licht in optisch dichteren Medien beobachtet, wo es sich mit einer geringeren Geschwindigkeit als c ausbreitet. Die Frequenz wird beim Übergang in optisch dichtere Medien nicht beeinflusst und folglich muss es laut
Mathematische BeschreibungDie formale Beschreibung der Elektromagnetische Wellen lässt sich auf die Maxwellschen Gleichungen zurückführen. Tatsächlich wurden elektromagnetische Wellen schon 1865 von James Clerk Maxwell theoretisch postuliert, bevor Heinrich Rudolf Hertz sie 1888 experimentell nachweisen konnte. An dieser Stelle sollen zunächst elektromagnetische Wellen im Vakuum betrachtet werden, also Wellen im ladungsfreien Raum unter Ausschluss von dielektrischen, dia- und paramagnetischen Effekten ( Man geht zunächst von der dritten Maxwellschen Gleichung aus (mit und wendet auf beide Seiten den Rotationsoperator an. Zum einen erhält man dadurch und setzt die vierte Maxwellsche Gleichung ein, Zum anderen gilt ganz allgemein die vektoranalytische Beziehung mit dem Laplace-Operator Δ
Wendet man diese Beziehung auf (1) an, und bedenkt man, dass der ladungsfreie Raum betrachtet wird, in dem nach der ersten Maxwellschen Gleichung die Divergenz von D Null ist, so ergibt sich:
Setzt man nun (2) und (3) zusammen, ergibt sich folgende Wellengleichung
Fast alle Wellen lassen sich durch Gleichungen der Form beschreiben, wobei v die Ausbreitungsgeschwindigkeit der Welle ist. Die Ausbreitungsgeschwindigkeit elektromagnetischer Wellen ist die Lichtgeschwindigkeit c. Für sie gilt daher
Damit erhält man also aus (4) die Gleichung die für jede Komponente eine Wellengleichung der Form (5) darstellt. Ihre Lösungen sind Wellen, die sich mit Lichtgeschwindigkeit c ausbreiten. Breitet sich die Welle in isotropen Materialien mit der Dielektrizitätskonstante ε und der Permeabilität μ aus, so ist die Ausbreitungsgeschwindigkeit c etwas niedriger, nämlich wobei aber im Allgemeinen die Materialkonstanten nicht linear sind, sondern selbst z. B. von der Feldstärke oder der Frequenz abhängen. Während das Licht sich in der Luft immer noch fast mit Vakuumlichtgeschwindigkeit c ausbreitet (die Materialkonstanten sind in guter Näherung 1), gilt das für Wasser schon nicht mehr, was u. a. den Tscherenkow-Effekt ermöglicht. Elektrostatische PotentialeWeiterhin ist auch eine mathematische Beschreibung mit Hilfe der Elektrostatischen Potentiale möglich, denn wegen und kann der Feldvektor der magnetischen Flussdichte auch als Rotation eines Vektorfeldes A aufgefasst werden. A wird deshalb das Vektorpotential von B genannt und es gilt: Diese Beziehung kann nun weiter verwendet werden. Die Rotation des elektrischen Feldes ist bestimmt durch Setzt man nun die eben gewonnene Beziehung aus (3) in (4) ein, so erhält man und daraus folgt Nun verschwindet aber die Rotation eines jeden Gradienten, so dass der innere Ausdruck von (6) als Gradient einer skalaren Funktion aufgefasst werden kann: Dieses kann nun wieder in den ursprünglichen Maxwell-Gleichungen im quellfreien Vakuum verwendet werden. Mit und (8) und der Beziehung (Graßmannscher Entwicklungssatz) erhält man Um diese Gleichungen (11) und (12) voneinander zu entkoppeln, wird verlangt, dass der Term unter dem Gradienten in (12) verschwindet (siehe Eichtransformation), also Ist die Bedingung aus (13) erfüllt, so ergibt sich aus (12) automatisch die Wellengleichung für das Vektorpotenzial A mit und aus (11) und (13) die Wellengleichung der skalaren Potenzialfunktion mit folgt Diese Beschreibung elektromagnetischer Phänomene kann durch Eichtransformation an verschiedene Probleme angepasst werden, um diese zu vereinfachen. Eine Kontroverse über die Rolle der Potenziale, insbesondere des Vektorpotenzials, lieferte der Aharonov-Bohm-Effekt. Hierbei fliegen Elektronen durch einen magnetfeldfreien Raum, werden aber dennoch beeinflusst. Man dachte, dass so das Vektorpotenzial, das auch im feldfreien Raum vorhanden war, direkt in Erscheinung tritt. In Wirklichkeit jedoch ist nur die Rotation des Vektorpotenzials entscheidend, und nach dem Satz von Stokes somit das Magnetfeld am Rand des feldfreien Raums. Alle anderen Deutungen und Behauptungen haben sich als falsch erwiesen. LiteraturClaus Müller: Grundprobleme der mathematischen Theorie elektromagnetischer Schwingungen, Springer Verlag, Heidelberg, 1957. Siehe auch
Kategorien: Elektrodynamik | Spektroskopie |
|
| Dieser Artikel basiert auf dem Artikel Elektromagnetische_Welle aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





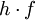 zugeordnet, wobei
zugeordnet, wobei 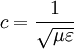 . Zudem wird sie abhängig von der Frequenz
. Zudem wird sie abhängig von der Frequenz 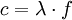 eine kürzere Wellenlänge haben. Da sich die Farbe aber im Medium nicht ändert, ist also nur die Frequenz charakteristisch für die Farbe des Lichts. In Spektren wird aus historischen Gründen jedoch immer noch die Wellenlänge als charakteristische Eigenschaft für Licht angegeben. Dieser Zusammenhang zwischen Farbe und Wellenlänge gilt dann aber nur im Vakuum (und in guter Näherung in Luft).
eine kürzere Wellenlänge haben. Da sich die Farbe aber im Medium nicht ändert, ist also nur die Frequenz charakteristisch für die Farbe des Lichts. In Spektren wird aus historischen Gründen jedoch immer noch die Wellenlänge als charakteristische Eigenschaft für Licht angegeben. Dieser Zusammenhang zwischen Farbe und Wellenlänge gilt dann aber nur im Vakuum (und in guter Näherung in Luft). 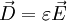 und
und 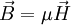 , siehe
, siehe 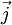 und
und 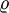 sind Null.
sind Null.
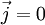 ):
):
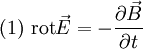
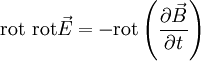
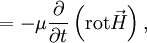
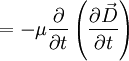
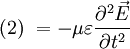
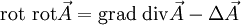
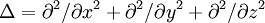 .
.

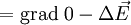
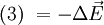 .
.
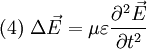 .
.
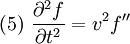
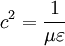 .
.