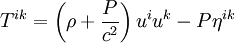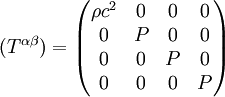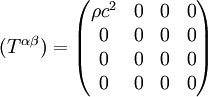Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Energie-Impuls-TensorDer Energie-Impuls-Tensor wird in seiner allgemeinen Form folgendermaßen angegeben: 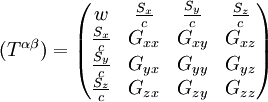
Im Rahmen der Speziellen Relativitätstheorie ist der so gegebene Energie-Impuls-Tensor ein Vierertensor der Stufe (2,0). Die Energiedichte w ist bei kleinen Geschwindigkeiten von der Dichte der Ruhemasse dominiert, aber auch Photonen, die keine Ruhemasse besitzen, tragen mit ihrer Energie E = hν zur Energiedichte bei. Eine Energiestromdichte ist eine Energiedichte multipliziert mit einer Geschwindigkeit. Produkt-Highlight
Geometrische raum-zeitliche Interpretation in 4D-SprechweiseZur Vereinfachung der Sprechweise wird in diesem Abschnitt die Konvention c = 1 (Normierung der Lichtgeschwindigkeit) verwendet. Aufgrund der Äquivalenz von Masse und Energie E = mc2 werden dann Masse und Energie miteinander identifiziert.
Die Symmetrie Tαβ = Tβα enthält folgende Information:
Die Energie-Impuls-Erhaltung in der Relativitätstheorie wird durch die Bilanzgleichung beschrieben, wenn Tαβ den Energie-Impuls-Tensor aller beteiligten Felder bezeichnet. Beschreibt Tαβ nur den Energie-Impulstensor eines Feldes, das mit anderen Feldern wechselwirkt, zum Beispiel der elektromagnetischen Strahlung alleine (s. unten), so lautet die Energie-Impuls-Bilanzgleichung
wobei die rechte Seite die Viererkraftdichte, also den Viererimpulsaustausch mit anderen Feldern pro 4D-Volumenelement bezeichnet. Die Komponenten β = 1,2,3 beschreiben hier die Impulsbilanz, die β = 0-Komponente die Energiebilanz (Massenbilanz). Differentialgeometrisch kann man den Energie-Impuls-Tensor als eine vektorwertige 3-Form auffassen: Jedem 3D-Volumenelement wird der Energie-Impuls-Vierervektor zugeordnet, der durch dieses 3D-Volumenelement hindurchfließt. Die Umrechnung in einen Vierertensor der Stufe (2,0) erfolgt dann mit dem Hodge-Operator. Der Energie-Impuls-Tensor in der Allgemeinen RelativitätstheorieDer Energie-Impuls-Tensor der Materie und Strahlung bildet die rechte Seite der Einstein-Hilbertschen Feldgleichungen und wirkt somit als „Quellterm“ für die Krümmung der Raum-Zeit. Neu gegenüber der Newtonschen Gravitationstheorie ist, dass alle Komponenten des Tensors die Rolle von „Quellen“ der Gravitation spielen, nicht nur die Massendichte T00. Bei moderaten Drücken, Scherspannungen und Geschwindigkeiten in Laborexperimenten bemerkt man das praktisch nicht, weil in natürlichen Einheiten gemessen die Massendichte der Materie meist um viele Größenordnungen größer als alle anderen Komponenten des Energie-Impulstensors ist. Der Energie-Impuls-Tensor der ElektrodynamikIm Lorentz-Heavisideschen EinheitensystemIn der Elektrodynamik im Heaviside-Lorentz-Einheitensystem (rationalisiertem Cgs) lautet der Energie-Impuls-Tensor des elektromagnetischen Feldes: (Im Gauß-Einheitensystem unterscheidet sich die Darstellung von der hier gegebenen um einen Faktor
Der Energie-Impulstrensor (Tαβ) ist eine Im SI-EinheitensystemDer Energie-Impuls-Tensor sieht in SI-Einheiten folgendermaßen aus:
Der Poynting-Vektor hat jetzt folgende Gestalt: (Die Umrechnung von der Darstellung im SI-System zum einfacheren Heaviside-Lorentz-Einheitensystem mit der Konvention c = 1 erfolgt einfach durch Weglassen der Konstanten ε0, μ0 und c.) Relativistische 4D-Notation für den elektromagnetischen Energie-Impuls-TensorIn relativistischer 4D-Notation kann man den Energie-Impuls-Tensor des elektromagnetischen Feldes wie folgt beschreiben:
Verwendete Notationen:
Bilanzgleichungen für den Energie-Impulstensor in der ElektrodynamikIn 3D-NotationIm folgenden bezeichnet
Die Maxwell-Gleichungen für das elektromagnetische Feld implizieren folgende Bilanzgleichungen für die Komponenten des Energie-Impulstensors: Die linke Seite stellt hier die lokale Energiebilanz des elektromagnetischen Feldes dar, und die rechte Seite die Leistungsdichte des elektromagnetischen Feldes am Materiefeld. Dieser Zusammenhang ist auch als Satz von Poynting bekannt.
Die linke Seite stellt hier die lokale Impulsbilanz des elektromagnetischen Feldes dar, und die rechte Seite die Lorentzsche Kraftdichte des elektromagnetischen Feldes am geladenen Materiefeld. In 4D-NotationIn speziell-relativistischer 4D-Notation kann man diese beiden Bilanzgleichungen auch so zusammenfassen:
Hierbei bezeichnet Die rechte Seite Der Energie-Impuls-Tensor der HydrodynamikDer Energie-Impuls-Tensor der Hydrodynamik geht in die Einsteinschen Feldgleichungen ein und ermöglicht die Angabe von Lösungen der Differentialgleichungen, mit denen die Dynamik des Kosmos beschrieben werden kann. Er wird in Lehrbüchern der theoretischen Physik, die Kapitel über Kosmologie enthalten, in der Regel in kontravarianter Darstellung folgendermaßen angegeben:
Diese Beschreibung des Energie-Impuls-Tensors setzt eine Menge von Flüssigkeits-Teilchen voraus, an die folgende Bedingungen gestellt werden: Es liegt eine ideale Flüssigkeit vor und der Druck ist isotrop im Ruhesystem eines jeden Teilchens. In der Kosmologie werden Galaxien als Elemente einer idealen kosmischen Flüssigkeit betrachtet. Die innere Expansion einer Galaxis wird dabei nicht betrachtet, sie entfernt sich auf Grund der kosmischen Expansion von allen anderen Galaxien, ein Beobachter, der sich mit dieser Galaxis mitbewegt, wird relativ zu ihr als ruhend betrachtet. In diesem Sinne ist eine Galaxie das Ruhesystem eines mitbewegten Beobachters. In einem solchen Ruhesystem reduziert sich der Vektor der Vierergeschwindigkeit zu (ui) = (c,0,0,0). Eine weitere Vereinfachung ergibt sich im Ruhesystem des Beobachters dadurch, dass der metrische Tensor (ηik) durch den metrischen Tensor der speziellen Relativitätstheorie ersetzt werden kann. Man betrachte als Beispiel den freien Fall eines Fahrstuhles. Der mitbewegte Passagier fühlt sich schwerelos. Er ruht in seinem mitbewegten System, das sich auf Grund der Erdgravitation bewegt. Dadurch vereinfacht sich der Energie-Impuls-Tensor: Verschwindet auch der Druck P, so besteht der Energie-Impuls-Tensor nur noch aus der Energie/Massendichte: Literatur
|
|
| Dieser Artikel basiert auf dem Artikel Energie-Impuls-Tensor aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





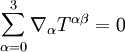
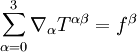 ,
,
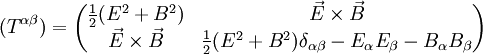
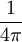 .)
.)
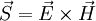 heißt
heißt 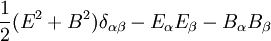 ,
, 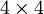 -Matrix, denn
-Matrix, denn 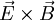 ist ein Vektor mit 3 Komponenten.
ist ein Vektor mit 3 Komponenten.
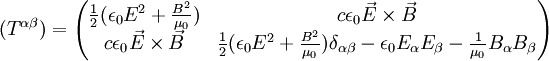
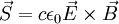
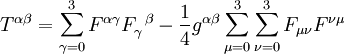 .
.
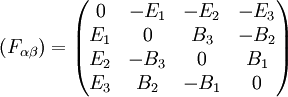 bezeichnet den
bezeichnet den 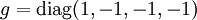 bezeichnet den metrischen Tensor der Speziellen Relativitätstheorie. Das Hoch- und Herunterziehen der Indizes erfolgt mit diesem Tensor.
bezeichnet den metrischen Tensor der Speziellen Relativitätstheorie. Das Hoch- und Herunterziehen der Indizes erfolgt mit diesem Tensor.
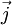 die elektrische Stromdichte eines geladenen Materiefeldes,
die elektrische Stromdichte eines geladenen Materiefeldes,
![\frac{\partial}{\partial t} \left[\frac12(E^2+B^2)\right]+\operatorname{div}\vec S =\vec j \cdot\vec E](images/math/b/e/7/be72228f83c1f20b92f4c428d9e01704.png)
![\frac{\partial}{\partial t} S_\beta+\sum_{\alpha=1}^3\frac{\partial}{\partial x_\alpha} \left[\frac{1}{2}(E^2+B^2) \delta_{\alpha\beta}-E_\alpha E_\beta-B_\alpha B_\beta \right]=(\vec j \times \vec B+ \rho\vec E)_\beta](images/math/6/6/b/66b4f29846bcfb2657610995f799ab8d.png) , (
, (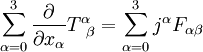 ,
, 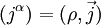 den Vierervektor des elektromagnetischen Viererstroms.
den Vierervektor des elektromagnetischen Viererstroms.
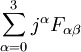 bekommt wieder die Interpretation einer Lorentzschen Viererkraftdichte (Viererimpulsübertrag pro 4D-Volumenelement).
bekommt wieder die Interpretation einer Lorentzschen Viererkraftdichte (Viererimpulsübertrag pro 4D-Volumenelement).