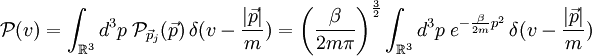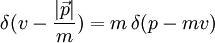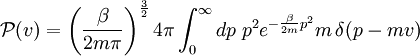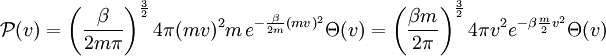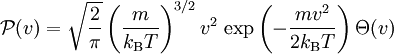Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Maxwell-Boltzmann-Verteilung
Die Maxwell-Boltzmann-Verteilung oder auch maxwellsche Geschwindigkeitsverteilung ist eine Wahrscheinlichkeitsverteilung der statistischen Physik und spielt in der Thermodynamik, speziell der kinetischen Gastheorie, eine wichtige Rolle. Sie beschreibt die Verteilung des Betrags In einem idealen Gas bewegen sich nicht alle Gasteilchen mit der gleichen Geschwindigkeit, sondern statistisch verteilt mit verschiedenen Geschwindigkeiten. Es wird hierbei keine Raumrichtung bevorzugt, die Bewegungsrichtung ist also rein zufällig (Brownsche Molekularbewegung). Mathematisch lässt sich dies so formulieren, daß die Komponenten des Geschwindigkeitsvektors Die Dichte der Verteilung von der Verteilungen der Komponenten. Die Verteilung des Betrags der Geschwindigkeit erhält man nun indem man die Wahrscheinlichkeit berechnet. Da der Integrand nur vom Betrag | x | abhängt, können wir schreiben Die Wahrscheinlichkeitsdichte von Die vereinfachende Voraussetzung eines idealen Gases innerhalb der Maxwell-Boltzmann-Verteilung gegenüber der Geschwindigkeitsverteilung der Teilchen eines realen Gases führen zu einer Abweichung, falls man diese auf reale Gase anwendet. Die Approximation der Maxwell-Boltzmann-Verteilung auf reale Gase ist hierbei umso besser, je schwächer der reale Charakter des Gases ist. Im Falle eines niedrigen Druckes und einer hohen Temperatur ist diese Näherung für die meisten Betrachtungen ausreichend. Produkt-Highlight
Formulierung der GeschwindigkeitsverteilungDie Dichte der Verteilung ist im dreidimensionalen Raum in zwei verschiedenen Schreibweisen gegeben durch: Hierbei stehen die einzelnen Formelzeichen für folgende Größen:
Bei einer eindimensionalen Betrachtung lautet die Maxwell-Boltzmann-Verteilung:
wobei die Geschwindigkeit v nur in eine Richtung respektive auch noch in die zugehörige Gegenrichtung weisen kann, also beispielsweise in +x-Richtung und -x-Richtung. Die Wahrscheinlichkeit w, dass ein Gasteilchen eine Geschwindigkeit zwischen v1 und v2 besitzt errechnet sich, unabhängig von der Dimension, aus: Der Anteil f der Teilchen in diesem Geschwindigkeitsintervall (Δv = v2 - v1) errechnet sich, als Näherung für ein möglichst kleines Geschwindigkeitsintervall, aus:
Bedeutung und AnwendungsbereichFolgerungen aus den Gleichungen
Alle anderen Größen bedingen, dass sich der Anteil der Teilchen bei einer bestimmten Geschwindigkeit immer im Intervall zwischen Null und Eins bewegt ([0,1]). Die beiden Abbildungen zur Rechten verdeutlichen die Abhängigkeit der Maxwell-Boltzmann-Verteilung von Teilchenmasse und Temperatur des Gases. Mit steigender Temperatur T nimmt die durchschnittliche Geschwindigkeit zu und die Verteilung wird gleichzeitig breiter. Mit steigender Teilchenmasse mM hingegen nimmt die durchschnittliche Geschwindigkeit ab und die Geschwindigkeitsverteilung wird gleichzeitig schmaler. Dieser Zusammenhang zwischen Teilchengeschwindigkeit und Temperatur bzw. Teilchengeschwindigkeit und Teilchenmasse/Molmasse ist hierbei auch quantitativ beschreibbar. Siehe hierzu den Abschnitt quadratisch gemittelte Geschwindigkeit. Bedeutung für die ThermodynamikDie Maxwell-Boltzmann-Verteilung erklärt beispielsweise den Prozess der Verdunstung. Beispielsweise kann feuchte Wäsche bei Temperaturen von 20°C trocknen, da es in dieser Verteilungskurve einen geringen Anteil von Molekülen mit der erforderlich hohen Geschwindigkeit gibt, welche sich aus dem Flüssigkeitsverband lösen können. Es wird also bei niedrigen Temperaturen immer einige Moleküle geben, die schnell genug sind, die Anziehungskräfte durch ihre Nachbarn zu überwinden und vom flüssigen oder festen Aggregatzustand in den gasförmigen Aggregatzustand überzugehen, was man als Verdampfung bzw. Sublimation bezeichnet. Umgekehrt gibt es aber auch unter den vergleichsweise schnellen Teilchen des Gases immer einige, die keine ausreichende Geschwindigkeiten besitzen und daher wieder vom gasförmigen in den flüssigen oder festen Aggregatzustand wechseln, was man als Kondensation bzw. Resublimation bezeichnet. Diese Vorgänge werden unter dem Begriff der Phasenumwandlung zusammengefasst, wobei sich zwischen Teilchen, die in die Gasphase eintreten, und Teilchen, die aus der Gasphase austreten, insofern es keine Störungen von außen gibt, ein dynamisches Gleichgewicht einstellt. Dieses ist Untersuchungsgegenstand der Gleichgewichtsthermodynamik, daher nennt man es auch thermodynamisches Gleichgewicht. Die Teilchen der gasförmigen Phase üben hierbei im Gleichgewichtszustand einen Druck aus, den man als Sättigungsdampfdruck bezeichnet. Grafisch dargestellt wird das Phasenverhalten von Stoffen in deren Phasendiagramm.
TeilchengeschwindigkeitenWahrscheinlichste GeschwindigkeitDie wahrscheinlichste Geschwindigkeit Mit dem Ergebnis: wobei:
Mittlere GeschwindigkeitDie mittlere Geschwindigkeit Hierbei sind vn (n = 1, 2, 3, ..., N) die einzelnen Geschwindigkeiten der Teilchen und N deren Gesamtzahl. Durch Substitution von v² = z und dv = dz / 2v und einmal partiell integrieren erhält man: Quadratisch gemittelte GeschwindigkeitDie quadratisch gemittelte Geschwindigkeit Aus der kinetischen Gastheorie ergibt sich folgende Zustandsgleichung: Die empirisch ermittelte Zustandsgleichung idealer Gase ist hierbei:
Setzt man den Ausdruck pV gleich erhält man: Umgestellt nach Hierbei zeigt sich, dass die quadratisch gemittelte Geschwindigkeit der Gasteilchen direkt proportional zur Quadratwurzel der Temperatur ist, insofern die Molmasse konstant bleibt, was jedoch im Allgemeinen der Fall ist. Daraus lässt, unter der Annahme einer konstanter Molmasse, ein wichtiger Grundsatz ableiten: Eine Verdopplung der Temperatur auf der Kelvin-Skala führt zu einer Erhöhung der quadratisch gemittelten Geschwindigkeit um den Faktor Durch diese Grundbeziehung lässt sich die Abhängigkeit der Temperatur von der Geschwindigkeit der Teilchen nicht nur qualitativ, sondern auch quantitativ ableiten. Die Temperatur ist also auf diesem Wege durch die kinetische Gastheorie definierbar. Zum gleichen Ergebnis kommt man auch, wenn man F(v) in folgende Gleichung substituiert und anschließend integriert: Die quadratisch gemittelte Geschwindigkeit ist dabei aber auch ein Maß für die mittlere kinetische Energie (Ekin) der Moleküle: Umgestellt ergibt sich hieraus: Beziehungen zwischen den GeschwindigkeitenIm Bild zur Linken ist die Maxwell-Boltzmannsche Geschwindigkeitsverteilung für Stickstoff (N2) bei drei verschiedenen Temperaturen abgebildet. Es ist auch die wahrscheinlichste Geschwindigkeit und die mittlere Geschwindigkeit eingezeichnet. Dabei gilt immer, dass die wahrscheinlichste Geschwindigkeit kleiner als die mittlere Geschwindigkeit ist. Allgemein gilt: 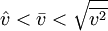 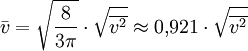
HerleitungDie Maxwell-Boltzmann-Verteilung lässt sich mit den Methoden der statistischen Physik herleiten. Man betrachtet ein N-Teilchensystem mit der Hamilton-Funktion dabei wird über die potentielle Energie U keine Annahmen gemacht, was bedeutet, dass folgende Herleitung auch für reale Gase gilt. Das System befinde sich im kanonischen Zustand mit der Phasenraumdichte und der kanonischen Zustandssumme
Der Parameter β ist proportional zur inversen Temperatur Der Erwartungswert einer klassischen Observable ist gegeben durch Für die Transformation von Wahrscheinlichkeitsdichten gilt: Gegeben sei eine Zufallsvariable X und eine Wahrscheinlichkeitsdichte
Alle Orts-Integrationen lassen sich kürzen, sowie alle Impuls-Integrationen
für Zur Auswertung dieses Ausdrucks nutzt man im Zähler die Faltungseigenschaft
der Delta-Distribution. Im Nenner integriert man über eine Gauß-Funktion
Damit lässt sich die Wahrscheinlichkeitsdichte für den Geschwindigkeitsbetrag
Die Integration führt man in Kugelkoordinaten durch und verwendet
die Relation Nun ist wieder die Faltungseigenschaft der Delta-Distribution zu verwenden dabei ist Θ(v) die Heaviside-Sprungfunktion, die die Wahrscheinlichkeit für negative Betragsgeschwindigkeiten verschwinden lässt. Setzt man für |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Maxwell-Boltzmann-Verteilung aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |


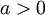
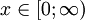
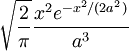
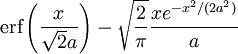
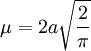
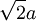
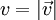 der Teilchengeschwindigkeiten' in einem
der Teilchengeschwindigkeiten' in einem 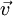 eines Gasteilchens der Masse "m" unabhängig voneinander und normalverteilt sind, mit den Parametern
eines Gasteilchens der Masse "m" unabhängig voneinander und normalverteilt sind, mit den Parametern
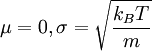
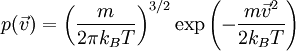
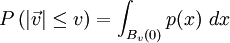
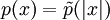 , und das Integral über die dreidimensionale Kugel
, und das Integral über die dreidimensionale Kugel 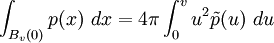
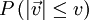 nach
nach 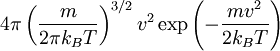


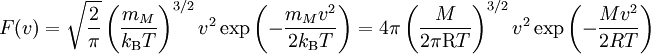
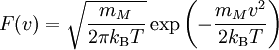 ,
,
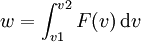
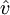 , also die Geschwindigkeit am Maximum der Verteilungsfunktion, berechnet sich aus
, also die Geschwindigkeit am Maximum der Verteilungsfunktion, berechnet sich aus
![\frac{dF(v)}{dv} = \left( \frac{m_\mathrm{M}}{2 \pi k_\mathrm{B} T} \right)^{3/2} \exp \left( \frac{-m_\mathrm{M} v^2}{2 k_\mathrm{B} T} \right) \left[ 8 \pi v + 4 \pi v^2 \left( \frac{-m_\mathrm{M} v}{k_\mathrm{B} T} \right) \right] = 0](images/math/8/4/e/84ef7bbca0f8e0e29f8830314c3ddc7c.png)
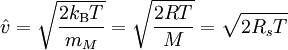
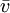 ist definiert durch:
ist definiert durch:
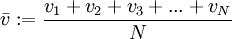
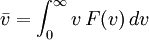
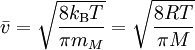
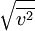 ist definiert durch:
ist definiert durch:
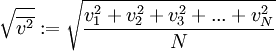
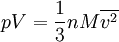
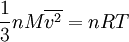
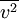 erhält man schließlich:
erhält man schließlich:
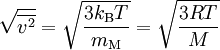
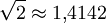 .
.
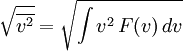

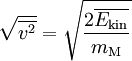
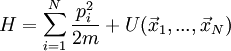
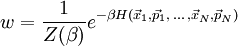
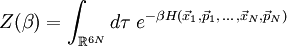 mit
mit 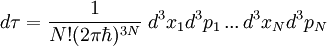
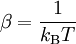
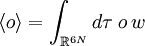
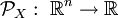 und eine Abbildung
und eine Abbildung 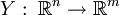 . Dann ist
. Dann ist 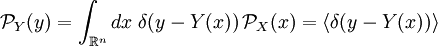 die Wahrscheinlichkeitsdiche der Zufallsvariablen
die Wahrscheinlichkeitsdiche der Zufallsvariablen 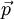 irgendeines Teilchens
irgendeines Teilchens 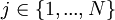 des Systems. Nach obigem Trafosatz gilt:
des Systems. Nach obigem Trafosatz gilt:
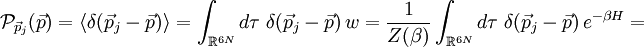
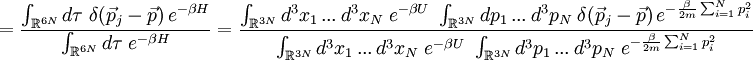
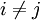 . Somit bleibt nur noch die
. Somit bleibt nur noch die 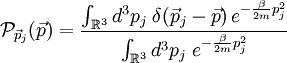
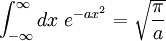 .
.
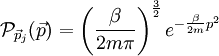
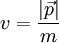 mit dem Trafosatz ermitteln
mit dem Trafosatz ermitteln