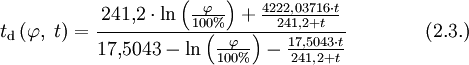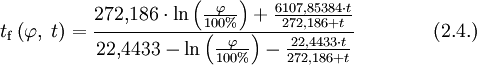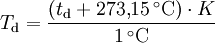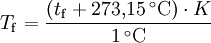Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
TaupunktTaupunkt und Reifpunkt bezeichnen die Zustände des Wassers in seinem Phasendiagramm, bei denen es zur Kondensation (zum Beispiel Taubildung) bzw. Resublimation (zum Beispiel Reifbildung) von Wasserdampf kommt. Es handelt sich also um den Kondensations- bzw. Resublimationspunkt des Wassers. In der Praxis ist der Taupunkt von Wasser der wohl am häufigsten gemessene Taupunkt. Allerdings haben auch flüchtige Kohlenwasserstoffe, wie Erdgas oder Lösemittel einen sogenannten Kohlenwasserstoff-Taupunkt, der, je nach Prozess, bedeutsam ist und nachgewiesen werden muss. Produkt-Highlight
Taupunkt
Der Taupunkt von Wasser im formalen Sinne ist der Kondensationspunkt reinen Wassers und damit ein Wertepaar aus Druck und Temperatur. Da sich diese jedoch an der Phasengrenzlinie eines Reinstoffes gegenseitig bedingen, hier im Speziellen der Kondensationskurve zwischen Tripelpunkt und kritischem Punkt, setzt man in der Regel den Temperaturwert des Taupunkts, also die Taupunkttemperatur, mit dem Taupunkt gleich. Es handelt sich dabei um diejenige Temperatur der feuchten Luft, bei der diese wasserdampfgesättigt wäre sowie bei einer zunehmenden Temperatursenkung kondensieren würde. In diesem Zustand würde die relative Luftfeuchte 100 Prozent betragen und es herrschte der Sättigungsdampfdruck. Demnach hat diese bzw. dieser auch das Formelzeichen Td bei Angaben in K und td oder Der Taupunkt als Maß für die Luftfeuchtigkeit ist eine abgeleitete, keine real vorliegende Temperatur und als solche normalerweise niedriger oder gleich der tatsächlichen Lufttemperatur. Sind beide gleich, so ist die Luft mit Wasserdampf gesättigt. Ein Feuchtemaß ist er deshalb, weil er abhängig vom Wasserdampfgehalt der Luft ist. Wird mit Wasserdampf gesättigte Luft unter den Taupunkt abgekühlt, so tritt Kondensation ein, welche sich in Beschlagen, Nebel, Tau bzw. allgemein in Niederschlag äußert. Einfach ausgedrückt: Je größer die Differenz zwischen Temperatur und Taupunkt ist, desto trockener ist die Luft. Wichtig für die Kondensation von Wasserpartikeln und die Vermeidung von größerer Übersättigung sind Aerosole als Kondensationskerne. Diese treten jedoch in der Regel überall in der Erdatmosphäre in ausreichender Anzahl auf, und verhindern dadurch größere Übersättigungen. Eine Besonderheit tritt während der Übersättigung ein, dann liegt die Taupunkttemperatur höher als die Lufttemperatur. Messtechnisch wird der Taupunkt mit dem Taupunktspiegelhygrometer bestimmt. TaupunktdifferenzDie Taupunktdifferenz (engl. auch spread genannt) ist ein weiteres Feuchtemaß und stellt die Differenz zwischen realer Luft- und Taupunkttemperatur dar. Je größer die Taupunktdifferenz, desto kleiner die relative Luftfeuchte und umgekehrt. Bei einer Differenz von Null, also identischer Luft- und Taupunkttemperatur, liegt Sättigung vor. In aufsteigender Luft verringert sich die Taupunktdifferenz, bis Sättigung erreicht ist. FrostpunktDer Frostpunkt, auch Eispunkt oder Reifpunkt genannt, stellt in Analogie zum Taupunkt ebenfalls ein Feuchtemaß dar, jedoch an der Phasengrenze fest-gasförmig, also im Bereich der Sublimation bzw. Resublimation. Man bezeichnet daher auch die zugehörige Phasengrenzlinie, welche sich vom absoluten Nullpunkt bis zum Tripelpunkt erstreckt, als Sublimationskurve. Das Formelzeichen des Frostpunktes ist Ti oder Tf für Angaben in K und ti bzw. Das ihm zurechenbare charakteristische Wetterphänomen, wiederum in Analogie zum Taupunkt, ist der Reif. Im Phasendiagramm des Wassers stellt der Frostpunkt den Temperaturwert der Sublimationskurve dar. Oft wird der Frostpunkt dem Taupunkt untergeordnet und dieser folglich als Sammelbegriff für beide Temperaturwerte verwendet. Berechnung von Taupunkt und FrostpunktAusgangspunkt für die Berechnung des Taupunkts bzw. Frostpunkts sind die Magnus-Formeln für den Sättigungsdampfdruck über Wasser (1.1.) und Eis (1.2.). Die Daten wurden hier bei D. Sonntag (1982) entnommen. wobei gilt: und für den Frostpunkt wobei gilt: Sättigungsdampfdruck und Taupunkt/Frostpunkt sind Größen, die sich gegenseitig bedingen, sie sind also als Funktion voneinander direkt berechenbar, wie die obigen Gleichungen für den Fall E(t) zeigen. Dies resultiert daraus, dass die Dampfdruckkurve im Phasendiagramm mit den Ausnahmen von kritischem Punkt und Tripelpunkt genau einen Freiheitsgrad besitzt, was sich wiederum aus der Gibbsschen Phasenregel ableitet. Man kann daher die obigen Gleichungen umstellen und erhält so den Taupunkt in Abhängigkeit vom Sättigungsdampfdruck über Wasser (1.3.) und den Frostpunkt in Abhängigkeit vom Sättigungsdampfdruck über Eis (1.4.). Es gilt zu beachten, dass auch diese Gleichungen aufgrund ihrer Ungenauigkeit nur in den begrenzten Temperaturintervallen der Ausgangsgleichungen verwendet werden sollten. Diese Intervalle wurden entsprechend den Stoffdaten des Wassers auf dessen Werte umgerechnet. Beide Gleichungen ergeben Temperaturwerte in Grad Celsius und sind für einen Sättigungsdampfdruck in hPa ausgelegt. wobei gilt: wobei gilt: Diese Formeln sind jedoch unpraktisch, da meist nur die relative Luftfeuchtigkeit und die zugehörige Lufttemperatur zur Verfügung stehen. Über die Gleichung (2.1.) beziehungsweise (2.2.) lässt sich jedoch auch ein direkter Zusammenhang zwischen den Größen herstellen. Nutzt man Gleichung (2.2.) und setzt in sie die Magnus-Formel (1.1.) ein, so erhält nach der Umstellung zum Taupunkt die Gleichung (2.3.), mit der sich dieser ausgehend von der relativen Luftfeuchtigkeit ( Diese lassen sich bei Bedarf auch in Kelvin umrechnen: Quellen und ReferenzenLiteraturD. Sonntag und D. Heinze 1982: Sättigungsdampfdruck- und Sättigungsdampfdichtetafeln für Wasser und Eis (1. Aufl.), Deutscher Verlag für Grundstoffindustrie |
|
| Dieser Artikel basiert auf dem Artikel Taupunkt aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





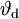 bei Angaben in
bei Angaben in 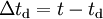
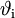 oder
oder 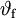 bei Angaben in
bei Angaben in 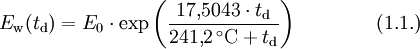
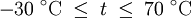
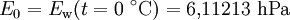
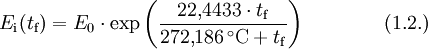
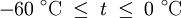
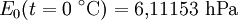
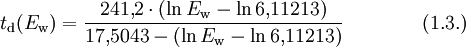
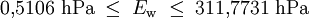
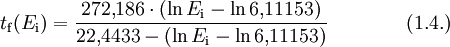
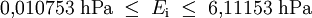
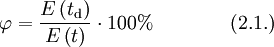
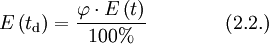
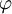 in %) und der Lufttemperatur (t in °C) berechnen lässt. Setzt man stattdessen Gleichung (1.2.) in (2.2.) ein, so erhält man nach dem Umstellen die Gleichung (2.4.) zur Berechnung des Frostpunkts, ebenfalls in Abhängigkeit von der relativen Luftfeuchtigkeit (
in %) und der Lufttemperatur (t in °C) berechnen lässt. Setzt man stattdessen Gleichung (1.2.) in (2.2.) ein, so erhält man nach dem Umstellen die Gleichung (2.4.) zur Berechnung des Frostpunkts, ebenfalls in Abhängigkeit von der relativen Luftfeuchtigkeit (