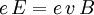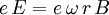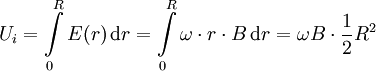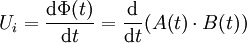Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
UnipolarinduktionUnipolarinduktion ist eine Form der elektromagnetischen Induktion. Sie tritt bei leitfähigen rotationssymmetrischen Körpern auf, wenn diese um ihre Achse rotieren und das Magnetfeld ebenfalls rotationssymmetrisch ist; beispielsweise bei einer Scheibe, die in einem zur Achse parallelen Magnetfeld rotiert. Unipolarinduktion erzeugt immer eine Gleichspannung, typischerweise mit geringer Spannung; es sind aber hohe Stromstärken möglich. Ihre Anwendung findet sie bei Unipolarmaschinen. Die Astrophysik behandelt den Effekt im Zusammenhang mit stellaren Magnetfeldern. Produkt-HighlightInduktionsgesetz und UnipolarinduktionBei nicht richtiger Anwendung des Induktionsgesetzes kann es zu Verständnisproblemen über die Ursachen der Unipolarinduktion kommen. Dieser Umstand wird in dem Faradaysches Paradoxon oder in dem Paradoxon von Hering zum Ausdruck gebracht und ist teilweise historisch durch die Begriffsbildung mit verursacht. Wesentlich für die korrekte Anwendung des Induktionsgesetzes ist es, dass die gedachte Linie an welcher entlang die induzierte Umlaufspannung ermittelt werden soll, fix mit dem elektrischen Leiter verbunden ist. Bei der Messung der Induktionsspannung zwischen dem außen stationär angebrachten Stromabnehmer im Punkt A und einem Punkt B, welcher am äußeren Umfang der Scheibe mitrotiert, kommt es bei einer zeitlich konstanten Drehzahl der Scheibe zu einer konstanten Vergrößerung der Verbindungslinie zwischen den Punkten A und B. Dieser zeitlich konstant anwachsende Abstand zwischen A und B vergrößert die Leiterschleife um welchen die Umlaufspannung gebildet werden muss. Weiters wird die Scheibe parallel zur Rotationsachse von einem konstanten magnetischen Fluss Φ durchflossen. Durch den zeitlich konstanten Anstieg der Wegstrecke zwischen A und B ist die zeitliche Änderungsrate (Ableitung) des Flusses Φ durch ein Flächenstück zwischen den Zentrum der Scheibe und den Punkten A und B eine Konstante C. Die zeitliche Änderungsrate entspricht dem Induktionsgesetz. Womit direkt aus dem Induktionsgesetz folgt, dass eine Gleichspannung an den Anschlussklemmen A und dem Zentrum der Scheibe liegen muss, welche direkt proportional der Konstante C ist. Alternativ kann die Induktionsspannung bei der Unipolarinduktion auch über die Lorentzkraft auf die Ladungsträger im rotierenden Körper erklärt werden, wie es im Folgenden dargestellt wird: Berechnung der Induktionsspannung für eine Scheibe
Im Folgenden wird angenommen, dass eine Scheibe mit der Winkelgeschwindigkeit ω um ihre Achse in einem homogenen achsparallelen Magnetfeld B rotiert. Es wird die Spannung zwischen der Achse und einem Schleifkontakt im Abstand R von der Achse gemessen. Die Lorentzkraft auf die freien Ladungsträger, die mit der Scheibe rotieren, steht im Gleichgewicht mit der Feldkraft in dem durch die Ladungstrennung erzeugten elektrischen Feld
Da
Durch Integration von E(r) ergibt sich die Induktionsspannung zwischen Mittelachse und dem Rand der Scheibe mit Radius R: Mit dem Induktionsgesetz erfolgt die Herleitung ohne Integralrechnung: Dabei ist α der Winkel (im Bogenmaß) des Kreissektors der Fläche A, der vom Magnetfeld durchsetzt wird. d/dt symbolisiert die zeitliche Ableitung. Das Vorzeichen in Ui ist weg gelassen, die Polung ergibt sich aus der Drei-Finger-Regel. Literatur
|
| Dieser Artikel basiert auf dem Artikel Unipolarinduktion aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





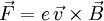
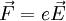
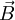 : Vektor der magnetischen Flussdichte
: Vektor der magnetischen Flussdichte
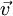 : Geschwindigkeitsvektor
: Geschwindigkeitsvektor