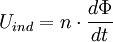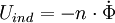Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Elektromagnetische InduktionUnter der elektromagnetischen Induktion (kurz: Induktion) versteht man das Entstehen einer elektrischen Spannung entlang einer Leiterschleife durch die Änderung des magnetischen Flusses. Die elektromagnetische Induktion wurde 1831 von Michael Faraday entdeckt bei dem Bemühen, die Funktionsweise eines Elektromagneten („Strom erzeugt Magnetfeld“) umzukehren („Magnetfeld erzeugt Strom“). Der Zusammenhang wird in seiner integrierten Form auch als das Faradaysche Gesetz bezeichnet und ist Teil der maxwellschen Gleichungen. Die Induktionswirkung wird technisch vor allem bei elektrischen Maschinen wie Generatoren, Elektromotoren und Transformatoren genutzt. Bei den meisten dieser Anwendungen treten Wechselspannungen auf. Es gibt aber auch Anwendungen, bei denen direkt und ohne eine Gleichrichtung Gleichspannungen durch die elektromagnetische Induktion entstehen, wie es bei der Unipolarinduktion der Fall ist. Zwei verschiedene Betrachtungsweisen der Induktion sind üblich: Die erste erklärt die Induktion mit Hilfe der Lorentzkraft und der Kraftwirkung auf bewegte elektrische Ladungsträger wie Elektronen. In bestimmten Situationen, wie bei magnetischen Schirmen oder der Unipolarinduktion, kann diese Vorstellung allerdings mit Problemen im Verständnis verbunden sein. Das zweite übliche Modell bedient sich Methoden aus der Feldtheorie und erklärt den Induktionsvorgang mit Hilfe der Änderung von magnetischen Flüssen und den damit verknüpften magnetischen Flussdichten. Produkt-Highlight
AllgemeinesDas Gesetz der elektromagnetischen Induktion, kurz Induktionsgesetz, beschreibt, unter welchen Bedingungen eine elektrische Spannung entlang einer elektrischen Leiterschleife hervorgerufen (induziert) wird. Eine Leiterschleife kann beispielsweise in Form einer in der Elektrotechnik genutzten Spule realisiert sein. Die zum Verständnis sinnvolle vektorielle Beschreibung gliedert sich in zwei mögliche Darstellungsformen:
Beide Darstellungsformen beschreiben ein und den selben Sachverhalt. Je nach konkreten Anwendungsfall und Problemstellung kann es sinnvoll sein, die eine oder die andere Form zu benutzen. Im Folgenden sind beide Darstellungsformen beschrieben. Induktionsgesetz in IntegralformEin zeitlich sich ändernder magnetischer Fluss induziert in einer ihn umgebenden Leiterschleife eine Spannung Uind. Diese Spannung lässt sich mittels eines Spannungsmessgerätes messen, wenn man die geschlossenen Leiterschleife auftrennt. Die eigentliche Induktionswirkung kommt dadurch zustande, dass ein zeitlich sich ändernder Fluss dΦ/dt vom einem elektrischen Wirbelfeld mit in sich geschlossenen Feldlinien umgeben ist. Dieses elektrische Wirbelfeld Etan, es spielt nur die tangentiale Feldkomponente eine Rolle, führt entlang eines infinitesimalen Stückes dr der Leiterschleife zu einer induzierten Spannung dUind:
Durch Summation aller infinitesimalen Spannungen längs der Leiterschleife ergibt sich die zwischen den Punkten rA und rB induzierte Spannung: Zieht man nun gedanklich die beiden Punkte rA und rB zusammen, so strebt die in der geschlossenen Leiterschleife mit der Kontur C (rA = rB) induzierten Spannung zu der induzierten Umlaufspannung Uuind: Der dritte Ausdruck ist die gleichwertige vektorielle Darstellung des tangentialen Feldstärkeanteils mit Hilfe des Skalarproduktes. Das Integral stellt ein so genanntes Ringintegral dar und soll kennzeichnen, dass über einen kompletten Umlauf entlang der Schleife C integriert wird. Die Umlaufspannung Uuind ist ident mit der bei Transformatorberechnungen verwendeten Windungsspannung welche die induzierte Spannung für eine Windung angibt. Die praktische Bedeutung der Umlaufspannung liegt darin, dass sich mit ihrer Hilfe die in Windungen von elektrischen Maschinen induzierten Spannungen berechnen lassen. Die Umlaufspannung ist der zeitlichen Änderungsrate des magnetischen Flusses direkt proportional und somit auch ein Maß für die Wirbelstärke des elektrischen Wirbelfeldes. Das negative Vorzeichen in obiger Gleichung ergibt sich aus der Lenzschen Regel: Die induzierte Feldstärke ist immer so gerichtet, dass eine von ihr bewirkte Stromänderung bzw. zugehörige Magnetfeldänderung der verursachenden Strom- bzw. Magnetfeldänderung entgegen wirkt. Da sich Flüsse nicht einzelnen Raumpunkten sondern nur Flächen A zuordnen lassen, drückt man den magnetischen Fluss meist durch die entsprechende magnetische Flussdichte B aus: so dass sich das Induktionsgesetz in der üblichen integralen Form schreiben lässt als: Für ruhende Leiter lässt sich die Reihenfolge der Integration bzw. Differentation vertauschen. Geschlossene elektrische Wirbelfelder existieren bei zeitlich veränderlichen magnetischen Flüssen nicht nur entlang der Leiterschleife sondern beispielsweise auch im Inneren des Eisenkernes eines Transformators. Sie sind dort die Ursache der meist unerwünschten Wirbelströme und der so genannten Wirbelstromverluste. Induktionsgesetz in DifferentialformDer Übergang von der Integralform in die Differentialform ist nichts anderes als die Überführung der globalen Wirbel- und Quellenstärken in lokale, diskrete Wirbel- bzw. Quellendichten welche einzelnen Raumpunkten (Punkten eines Vektorfeldes) zugeordnet sind. In der Integralform sind es dimensionsbehaftete Zahlenwerte wie der magnetische Fluss, in der Differentialform des Induktionsgesetzes wird der Übergang auf Funktionen im Bezug zur Funktionentheorie vollzogen. Ausgegangen wird vom globalen Induktionsgesetz für ruhende Körper, wobei die Einschränkung auf ruhende Körper im folgenden wesentlich ist: Wird nun die Fläche der Kontur C in jener Gleichung laufend verkleinert, man lässt sie gegen Null streben um einen Punkt zu erhalten, strebt auch die zugehörige Wirbelstärke gegen Null. Ein Ausweg besteht darin, vor dem Übergang ein Verhältnis der Wirbelstärke mit der zugeordneten berandeten Fläche zu bilden und im weiteren mit diesem Verhältnis zu arbeiten. Der Wert dieses Punktes bleibt dann endlich und ist eine charakteristische Eigenschaft des betrachteten Feldpunktes, womit die lokale Form gebildet ist. Mathematisch wird dieser Weg dahin beschritten, dass obige Gleichung in Relation (Verhältnis) mit einem vektoriellen Flächenelement A′, dessen Normalenvektor n in Flussrichtung zeigt, gesetzt wird, und dann eine Grenzwertbestimmung für A′ → 0 erfolgt. Damit entfällt die Integration durch das Flächenintegral: Die dabei auftretende, und zunächst kompliziert wirkende Abfolge von links beginnend mit Integration, gefolgt von der Division und Grenzwertbildung, drückt man in der Vektoranalysis zusammengefasst als speziellen Vektoroperator mit der Bezeichnung rot (für Rotation, engl. curl) aus, womit die differentielle Darstellung des Induktionsgesetzes die Form: annimmt. Die lokale Wirbeldichte rot E des elektrischen Feldes E ist somit gleich der negativen zeitlichen Änderung der lokalen magnetischen Flussdichte B. Für die praktische Anwendung ist wichtig, dass sich die Vektoroperationen wie rot auf ein bestimmtes Koordinatensystem beziehen. Dies wurde in obiger Gleichung implizit durch den Normalenvektor von A′ vorweggenommen. Je nach frei wählbaren Koordinatensystem ergeben sich für die Vektoroperation verschiedene Darstellungen. Anwendung auf verschiedene GeometrienDas Induktionsgesetz beschreibt das Auftreten der Induktion bei verschiedenen Geometrien:
Unterbrochene metallische LeiterschleifeIm einfachsten Fall liegt eine metallische Leiterschleife mit Unterbrechung vor. Da das Metall im Vergleich zu der Unterbrechung eine sehr gute elektrische Leitfähigkeit besetzt, fällt entlang der Leiterschleife (von 1' nach 1) keine elektrische Spannung ab. Die gesamte Umlaufspannung fällt an den Klemmen als Spannung ab. Vergrößert sich das B-Feld während des Zeitschrittes dt, so liegt eine Vergrößerung des Magnetischen Flusses Verringert sich das B-Feld während des Zeitschrittes dt, so liegt eine Verringerung des Flusses Bei der Beschreibung wurde selbstverständlich eine Integration in positiver Zeitrichtung (dt > 0) vorausgesetzt. Geschlossene ideal-leitende Leiterschleife
Eine geschlossene Leiterschleife mit idealer Leitfähigkeit verhindert, dass sich der magnetische Fluss durch die Leiterschleife ändert, denn wegen der idealen Leitfähigkeit des Metalls ist das Umlaufintegral der Spannungen gleich Null, und es gilt: Das Entstehen der Flussänderung wird durch die in der Leiterschleife induzierten Ströme verhindert. In der Praxis ist der elektrische Widerstand der Kurzschlussschleife geringfügig größer als Null. Beträgt der elektrische Widerstand des Leiters R, so gilt: Wegen des geringen Widerstands des elektrischen Leiters fließen hohe elektrische Ströme, die dem magnetischen Feld die Momentanleistung Die Aussage, dass der Strom i(t) seiner Ursache entgegenwirkt, ist im Sinne des gewählten Beschreibungsmodells problematisch. Tatsächlich fließt bei steigendem magnetischen Fluss wegen des Minuszeichens im Induktionsgesetz ein Strom entgegen der eingezeichneten positiven Stromrichtung i(t). Dieser Strom erzeugt gemäß dem Durchflutungssatz eine magnetische Feldstärke H, die andersherum zeigt als das B-Feld.
Es ist jedoch zu beachten, dass das Induktionsgesetz nicht zwischen Selbsterregung und Fremderregung unterscheidet. Insofern ist die Kompensationswirkung des induzierten Stromes schon im magnetischen Fluss Ist das B-Feld von außen aufgeprägt, so ändert sich der Fluss durch den entstehenden induzierten Strom nicht. Vielmehr kompensiert die Quelle, die das Magnetfeld erzeugt, die durch den induzierten Strom erzeugte Flussänderung instantan, indem sie zusätzliche Energie zur Aufrechterhaltung des B-Feldes bereitstellt. Diese Situation liegt in sehr guter Näherung beispielsweise beim Transformator mit eingeprägter Primärspannung vor. Sobald im Sekundärkreis ein Strom fließt, erhöht sich in der primärseitigen Spannungsquelle der Quellenstrom, so dass der magnetische Fluss im gemeinsamen Kern konstant bleibt. Induktionsspannung durch Bewegen eines elektrischen Leiters in einem Magnetfeld (1. Induktionsphänomen)Wenn ein elektrischer Leiter in einem Magnetfeld bewegt wird, entsteht nur dann eine Induktionsspannung, wenn er sich nicht in Feldrichtung bewegt (parallel zu den Feldlinien). Zu beachten ist dabei, dass in diesem Kontext unter dem Begriff „elektrischer Leiter“ die fix mit dem Leiter aber nur gedachte Kontur (Leiterschleife) wesentlich ist und nicht direkt ein bestimmter meist metallischer Leiter in Form eines Drahtes oder ähnliches. Diese begriffliche Trennung ist deswegen notwendig, da es sonst bei bestimmten Induktionsphänomenen, und bei allgemeiner Anwendung des Induktionsgesetzes welche durch mechanische Bewegungen im Magnetfeld ausgelöst werden wie der Unipolarinduktion, zu Verständnisschwierigkeiten kommt. Man erreicht eine maximale Spannung, wenn sich der elektrische Leiter senkrecht zum Magnetfeld bewegt (siehe auch Drei-Finger-Regel). Da sowohl Geschwindigkeit als auch magnetische Flussdichte vektorielle Größen sind, muss das Vektorprodukt gebildet werden. (Daher auch der Faktor Nach der Lenzschen Regel entsteht die Induktionsspannung, um durch den durch sie bewirkten Stromfluss wiederum ein Magnetfeld zu erzeugen, welches die äußere Magnetfeldänderung kompensiert, so dass eine Induktion also immer ihrer Ursache entgegen wirkt. Dies schlägt sich im negativen Vorzeichen der folgenden Gleichungen nieder. Die erzeugte Spannung ist dabei:
Sobald der elektrische Leiter sich im Magnetfeld bewegt, wirkt auf die Ladungen im elektrischen Leiter eine Kraft, die Lorentzkraft. Somit werden sie getrennt. Die Spannung hängt dann nur noch von der Größe dieser Kraft ab. Die Kraft (auf eine Ladung) wiederum hängt nur von der Geschwindigkeit und vom Magnetfeld ab. Es ergibt sich obige Gleichung. Induktionsspannung durch Änderung des magnetischen Flusses (2. Induktionsphänomen)Induktionen treten nicht nur auf, wenn sich elektrische Leiter in einem Magnetfeld bewegen, sondern auch, wenn sich das magnetische Feld verändert. Um dies zu verstehen, muss man eine Modellgröße einführen: den magnetischen Fluss. Dieser ist für ein homogenes Feld definiert als: wobei A die Fläche der Stromschleife, deren Raumorientierung durch ihren Normalenvektor angegeben ist. Für die induzierte Spannung gilt: Dabei ist n die Anzahl der Windungen der Spule. Wenn sich nun entweder das Magnetfeld ändert (schwächer oder stärker) oder die Fläche kleiner oder größer wird, ändert sich auch der magnetische Fluss. Diese Änderung wird durch die Ableitung nach der Zeit dargestellt und daraus ergibt sich die induzierte Spannung. Der Faktor -n gibt zum Einen die Vergrößerung der Spannung an, je mehr Windungen eine Spule im Feld hat, und zum Anderen im Vorzeichen die Lenzsche Regel, die besagt, dass der Induktionsstrom (bzw. die Spannung) immer der Ursache entgegen wirkt. Satz: Ändert sich der magnetische Fluss:
der eine Spule von n Windungen durchsetzt, in der Zeitspanne dt um dΦ, so wird in dieser Spule die mittlere Spannung: induziert (nach Faraday), die so gepolt ist, dass der von ihr getriebene Strom der Ursache des Induktionsvorganges entgegenwirken kann (nach Lenz). Momentanwert durch Ableiten nach der Zeit: Technische Anwendungen
Eine Spannung wird induziert, solange sich das von der Spule umfasste Magnetfeld ändert. Eine Induktionsspannung ist nur dann vorhanden, wenn sich der magnetische Fluss ändert. Da der Fluss das Produkt aus Flussdichte und Fläche ist, kann sich dazu entweder die Flussdichte B oder die Fläche A ändern. Eine Änderung der Fläche wird erreicht, indem man z. B. die Spule in einem konstanten Magnetfeld oder einen Magneten in einer Spule dreht. Die vom Magnetfeld durchsetzte Fläche ist null, wenn die Spule quer zum Magnetfeld steht, sie ist maximal, wenn das Feld die Spule axial durchsetzt. Nach diesem Prinzip wird in einem Generator (Dynamomaschine) Strom erzeugt. Eine Änderung der Flussdichte erreicht man durch ein veränderliches Magnetfeld. Nach diesem Prinzip wird in der Sekundärwicklung eines Transformators bei Speisung der Primärwicklung mit einer Wechselspannung eine Wechselspannung induziert, deren Höhe proportional zum Verhältnis der Windungszahlen ist. Hierunter fallen auch alle Arten der induktiven Erwärmung durch Wirbelstrom: der Induktionsofen, Induktionshärten und der Induktionsherd usw. Induktive Erwärmung von Werkstoffen: Induktionsöfen werden vorwiegend in der Industrie zum Härten, Löten, Schmelzen usw. eingesetzt. Diese Technik kommt zunehmend in der privaten Anwendung beispielsweise in der Küche als Induktionsherd zum Gebrauch. SelbstinduktionAusgehend vom Indunktionsgesetz erzeugen extern einwirkende, zeitlich veränderliche magnetische Flüsse in zeitlich konstanten Leiterschleifen zeitlich veränderliche elektrische Spannungen. Bei einem geschlossenen Stromkreis der Leiterschleife entstehen zeitlich veränderliche elektrische Ströme welche ihrerseits, wie bei jedem Strom, zeitlich veränderliche magnetische Flüsse verursachen. Welche sich dem von extern aufgebrachten magnetischen Fluss überlageren. Diese Umstand wird allgemein als Selbstinduktion bezeichnet. Grundsätzlich kann auch die Selbstinduktion vollständig durch das Induktionsgesetz beschrieben werden und erfordert keine formale Ergänzungen oder Anpassungen. Allerdings kommt es bei der in Elektrotechnik üblichen Netzwerktheorie, welche beispielsweise zur Beschreibung von elektrischen Maschinen wie Transformatoren Verwendung findet, unter Umständen zu Verständnisschwierigkeiten, da die Netzwerktheorie keine Feldgrössen wie den magnetischen Fluss kennt. Statt dessen wird mit zeitlich veränderlichen Spannungen und Strömen in Ersatzschaltbildern mit passiven Bauelemente wie Spulen und elektrischen Widerständen gearbeitet. Die induzierten Spannugen werden als Spannungsquellen modelliert, welche historisch auch als elektromotorische Kraft (EMK) bezeichnet werden. Da es sich bei induzierten Spannungen aber um keine Kraft im physikalischen Sinn handelt, sollte dieser Begriff vermieden werden. Im Netzwerkmodell, wie sie unter anderem Schaltpläne darstellen, wird weiters mit Zählpfeilen und bestimmten Orientierungen gearbeitet wie es zur Verdeutlichung nebenstehende Abbildung darstellen. Zur Verdeutlichung ist der von extern auf die Leiterschleife einwirkende magnetische Fluss Φext und die davon verursachten induzierten Spannungen uext mit dem Index ext versehen. Bei Belastung der extern geschlossenen Schleife fliessende Strom i erzeugt einen magnetischen Fluss ΦI, welcher mit dem Index I kennzeichnet ist. Die selbstinduzierte Quellenspannung lässt sich als eine Spannungsquelle mit dem Betrag ui modellieren, wie in erster Abbildung dargestellt, und ist der dem Spulenstrom i treibenden Spannung uext entgegengerichtet. Man bezeichnet sie daher auch als Gegenspannung. Anwendung findet diese Darstellung beispielsweise bei der Beschreibung des so genannten Magnetisierungsstromes bei einem Transformator. Das Modell des induktiven Spannungsabfalles, wie in zweiter Abbildung dargestellt, kommt ohne weiterer Spannungsquelle aus. Die an der eingezeichneten Spule L auftretende Spannung weist dabei in die gleiche Richtung wie der Strom i welcher durch die von extern treibenden Spannung uext verursacht ist. Diese Darstellung hat den Vorteil, dass die Zusammenhänge im Netzwerkmodell bei harmonischen Vorgängen durch das Ohmsches Gesetz mit Blindwiderständen einfacher beschrieben werden können. Der in der Elektrotechnik wichtige Spezialfall von harmonischen Vorgängen bei den auftretenten Grössen reduziert die zeitlichen Ableitungen im Induktionsgesetz auf Multiplikationen mit jω (dΦ/dt ≡ jωΦ), was in der komplexen Ebene einer Drehung um 90° entspricht. AnwendungenDie Selbstinduktion wird unter anderem genutzt, um mit einer Zündspule den Zündfunken bei Ottomotoren oder die erforderliche hohe Zündspannung bei Leuchtstofflampen zu erzeugen. Erweiterungen und geschichtliche EntwicklungDie dargestellte elektromagnetische Induktion als Teil der maxwellschen Gleichungen und der klassischen Elektrodynamik (KED) spiegelt den Kenntnisstand aus dem Ende des 19. Jahrhunderts wider. Es wurden damals teilweise nur andere Begriffe und Nomenklaturen für die Darstellungen benutzt, die grundlegenden Vorstellungen über den Induktionsvorgang waren vorhanden. Anfang des 20. Jahrhunderts erfolgte die relativistische Eingliederung des Induktionsgesetzes im Rahmen der speziellen Relativitätstheorie und es wurde auf die Verhältnisse bei Geschwindigkeiten nahe der Lichtgeschwindigkeit Rücksicht genommen. Dabei ändern sich beispielsweise die Beträge der elektrischen und magnetischen Feldkomponenten in Abhängigkeit der Bewegung zwischen einem Beobachter und einer beobachteten elektrischen Ladung. Diese Abhängigkeiten in der relativen Bewegung zueinander zwischen verschiedenen Bezugsystemen werden durch die Lorentz-Transformation beschrieben. Dabei zeigt sich, dass das Induktionsgesetz, so wie die restlichen maxwellschen Gleichungen, „lorentzinvariant“ ist. Das heisst, die Gleichungen werden durch die Lorentz-Transformation zwischen verschiedenen Bezugsystemen nicht verändert. Dabei wird auch besonders deutlich, dass die elektrischen und magnetischen Felder nur zwei Erscheinungsformen ein und des selben Phänomen sind. Mitte des 20. Jahrhunderts gelang im Rahmen der Elektrodynamik die Verbindung der Quantenmechanik mit der speziellen Relativitätstheorie und es wurde auch das Induktionsgesetz im Rahmen einer Quantenfeldtheorie des Elektromagnetismus formuliert. Diese Quantenfeldtheorie wird als Quantenelektrodynamik (QED) bezeichnet. Sie stellt heute, auch aufgrund des grossen technischen Anwendungsgebietes, eine der durch Experimente am genauesten überprüfte Theorie der Physik dar. Literatur
Kategorien: Magnetismus | Elektrodynamik |
|
| Dieser Artikel basiert auf dem Artikel Elektromagnetische_Induktion aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |





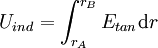
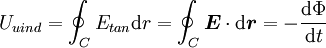
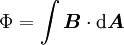
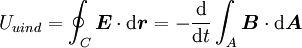
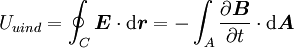
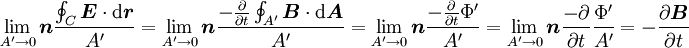
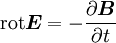
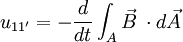
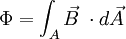 vor, da das B-Feld und die Fläche dA in die gleiche Richtung zeigen. Dem Minuszeichen im Induktionsgesetz entsprechend ist die Spannung
vor, da das B-Feld und die Fläche dA in die gleiche Richtung zeigen. Dem Minuszeichen im Induktionsgesetz entsprechend ist die Spannung 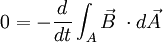
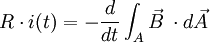
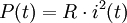 entziehen und die Leiterschleife erhitzen. Nach diesem Prinzip arbeiten u. a. Induktionsbremsen und Induktionsherde. Bei Induktionsbremsen stammt die Energie, die für die Aufrechterhaltung des B-Feldes kommt, aus der Bewegung des zugehörigen Fahrzeugs. Diese nimmt stetig ab, bis das Fahrzeug sich verlangsamt hat.
Bei Induktionsherden stammt die Energie zur Aufrechterhaltung des Magnetfeldes aus dem Haushaltsnetz.
entziehen und die Leiterschleife erhitzen. Nach diesem Prinzip arbeiten u. a. Induktionsbremsen und Induktionsherde. Bei Induktionsbremsen stammt die Energie, die für die Aufrechterhaltung des B-Feldes kommt, aus der Bewegung des zugehörigen Fahrzeugs. Diese nimmt stetig ab, bis das Fahrzeug sich verlangsamt hat.
Bei Induktionsherden stammt die Energie zur Aufrechterhaltung des Magnetfeldes aus dem Haushaltsnetz.
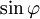 .)
.)
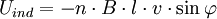
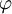 = Winkel zwischen Geschwindigkeitsvektor und magnetischer Flussdichte
= Winkel zwischen Geschwindigkeitsvektor und magnetischer Flussdichte
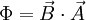
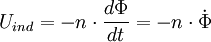
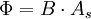 ,
,