Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
Würfel (Geometrie)Der Würfel (auch gleichseitiges Hexaeder [hɛksaˈeːdər], von griech. hexáedron, „Sechsflächner“, oder Kubus, von lat. cubus, „Würfel“) ist einer der fünf platonischen Körper, genauer ein (dreidimensionales) Polyeder (ein Vielflächner) mit
Der Würfel ist ein spezielles (dreidimensionales) Parallelepiped (Parallelflach), ein spezieller (nämlich gleichseitiger) Quader sowie ein spezielles gerades quadratisches Prisma. Produkt-Highlight
SymmetrieWegen seiner hohen Symmetrie – alle Ecken, Kanten und Seiten sind untereinander gleichartig – ist der Würfel ein reguläres Polytop. Er hat
und ist
Für eine vierzählige Drehachse gibt es 3 Symmetrieoperationen (Drehung um 90°, 180° und 270°), für eine dreizählige Drehachse dementsprechend 2 Symmetrieoperationen.
Insgesamt hat die Symmetriegruppe des Würfels 48 Elemente. Man bezeichnet sie in der Notation von Schönflies als Oh, in der Notation von Hermann / Mauguin als Beziehungen zu anderen PolyedernDer Würfel ist das zum Oktaeder duale Polyeder (und umgekehrt). Außerdem beschreiben die Eckpunkte des Würfels zwei punktsymmetrische reguläre Tetraeder, welche zusammen das Sterntetraeder als weiteren regulären Körper bilden. Mithilfe von Würfel und Oktaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Würfelgruppe als Symmetriegruppe haben. So erhält man zum Beispiel
als Durchschnitte eines Würfels mit einem Oktaeder (siehe archimedische Körper) und
als konvexe Hülle einer Vereinigung eines Würfels mit einem Oktaeder. Der Würfel ist Baustein der regulären Würfelparkettierung. Formeln
Hexaeder in der ChemieEine organische Verbindung, die wie ein Würfel aufgebaut ist, ist das nach dem englischen Cube (engl. für Würfel) benannte Cuban. VerallgemeinerungAuch die Analoga des Würfels in beliebiger Dimension n werden als (n-dimensionale) Würfel (oder Hyperwürfel) bezeichnet und sind ebenfalls reguläre Polytope.
Der n-dimensionale Würfel hat
Ein Modell für den n-dimensionalen Würfels ist der Einheitswürfel In im Vektorraum Rn. Und zwar ist der abgeschlossene Einheitswürfel
Der Einheitswürfel ist ein achsenparalleler Würfel mit der Kantenlänge 1 und einer Ecke im Koordinatenursprung. Eine Verallgemeinerung dieses Konzepts sind Quader im Rn, die in der mehrdimensionalen Analysis eine Rolle spielen. |
||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Würfel_(Geometrie) aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. | ||||||||||||||||





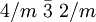 oder allgemein aber etwas ungenau als Oktaeder- bzw. Würfelgruppe.
oder allgemein aber etwas ungenau als Oktaeder- bzw. Würfelgruppe.
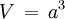
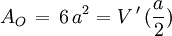
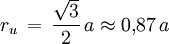
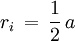
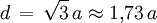
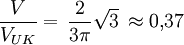
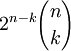 begrenzende Seiten der Dimension k. Spezialfälle:
begrenzende Seiten der Dimension k. Spezialfälle:
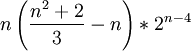 Volumen (k=3) und
Volumen (k=3) und 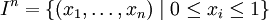
![I^n = [0,1] \times \cdots \times [0,1]](images/math/f/c/7/fc75e9dfe32a2bca4375e3599180394b.png) , das n-fache kartesische Produkt des Einheitsintervalls
, das n-fache kartesische Produkt des Einheitsintervalls
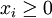 und
und