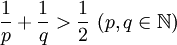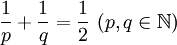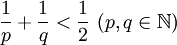Platonischer Körper

Die platonischen Körper (oder regulären Polyeder) sind die nach Platon benannten fünf besonders regelmäßigen konvexen Polyeder (Vielflächner), die dadurch charakterisiert sind, dass ihre Seitenflächen zueinander kongruente regelmäßige Vielecke sind, von denen in jeder Ecke jeweils gleich viele zusammentreffen. Sie werden deswegen auch reguläre oder regelmäßige Körper genannt.

Ihre Namen stammen aus dem Griechischen und beziehen sich auf die Anzahl ihrer Flächen: Tetraeder (vier Dreiecke), Hexaeder (das ist der Kubus oder Würfel) (sechs Quadrate), Oktaeder (acht Dreiecke), Dodekaeder (zwölf Fünfecke) und Ikosaeder (zwanzig Dreiecke).

Eine etwas allgemeinere Gruppe sind die 13 so genannten semiregulären oder archimedischen Körper.

In diesem Artikel liegt der Schwerpunkt hauptsächlich auf den gemeinsamen Eigenschaften und den Beziehungen der Körper untereinander. Eingehender werden die einzelnen Körper unter ihren jeweiligen Einträgen behandelt.

Weiteres empfehlenswertes Fachwissen

Wie erhalten Sie Tag für Tag genaue Wägeresultate?

Wie kann man Pipetten schnell überprüfen?

Richtiges Wägen mit Laborwaagen: Die Wägefibel

Die fünf platonischen Körper

Grundlegende Eigenschaften

Anzahl der platonischen Körper

Je zwei platonische Körper vom selben Typ sind zueinander ähnlich, d.h., ein platonischer Körper ist durch die Angabe einer einzigen Größe, beispielsweise Kantenlänge, Körpervolumen oder Umkreisradius bereits eindeutig bestimmt. In diesem Sinne ist es also gerechtfertigt von dem Tetraeder, dem Hexaeder usw. zu sprechen.

Unter den Bedingungen, dass die Oberfläche nur aus gleichen und regelmäßigen Polygonen besteht, und der Körper konvex (frei von Einbuchtungen) sein soll, gibt es genau fünf platonische Körper. Der Beweis dafür findet sich schon bei Euklid. Er beruht auf folgenden Überlegungen:

Für jede Polyederecke ist die Summe der Innenwinkel aller angrenzenden Flächen kleiner als 360°. Wäre sie genau 360°, würden die Flächen in einer Ebene liegen; auch bei mehr als 360° wäre keine Ecke möglich.

Andererseits müssen sich an jeder Ecke eines Polyeders mindestens drei Flächen treffen.

Sind also bei einem Körper alle Seitenflächen gleichseitige Dreiecke (Innenwinkel 60°), so können daher an einer Ecke drei, vier oder fünf Dreiecke (Winkelsumme 180°, 240°, 300°) zusammentreffen. Sind die Seitenflächen Quadrate (Innenwinkel 90°) oder regelmäßige Fünfecke (Innenwinkel 108°), so können davon jeweils drei zusammentreffen (Winkelsumme 270° bei Quadraten bzw. 324° bei Fünfecken). Sechs gleichseitige Dreiecke, vier Quadrate und drei regelmäßige Sechsecke (Innenwinkel 120°) ergeben jeweils genau 360°, sodass keine Ecke im Raum entsteht, sondern reguläre Parkettierungen der Ebene. Alle anderen Möglichkeiten (vier regelmäßige Fünfecke, drei regelmäßige Siebenecke, etc.) überschreiten diesen Winkel bereits.

Bei drei bzw. vier gleichseitigen Dreiecken und bei drei Quadraten pro Ecke ist leicht zu sehen, dass es entsprechende Körper tatsächlich gibt.

Beim Ikosaeder und Dodekaeder ist nicht unmittelbar klar, dass die Vielecke sich lückenlos und überschneidungsfrei zusammenschließen. Um dies zu belegen, dienen noch folgende Überlegungen:

Ein Ikosaeder – bei dem fünf gleichseitige Dreiecke in einer Ecke zusammenstoßen – kann man wie folgt konstruieren:

Man verbindet bei zwei Fünfecken, die parallel zueinander liegen und die gegeneinander verdreht sind, jeweils die „verdrehten“ Ecken so miteinander, dass zehn gleichseitige Dreiecke entstehen (formal ausgedrückt: man bildet zu einem Fünfeck ein Antiprisma). Setzt man auf die Basis und auf die Deckfläche jeweils eine fünfseitige Pyramide (mit fünf gleichseitigen Dreiecken als Mantel) auf, so erhält man einen Körper mit 12 Ecken und 20 gleichseitigen Dreiecken. Es zeigt sich (z.B. durch Nachrechnen), dass die beiden den Pyramidenspitzen entsprechenden Ecken und die zehn Ecken des Antiprismas kongruent (mit gleichen Flächenwinkeln) sind, also tatsächlich ein völlig regelmäßiges (ein reguläres) Polyeder vorliegt. Das Dodekaeder ergibt sich dann als duales Polyeder. (Ohne diese Überlegung ist es nicht selbstverständlich, dass das Dodekaeder tatsächlich durch ebene Fünfecke realisiert werden kann.)

Die fünf oben gezeigten platonischen Körper sind also (bis auf Ähnlichkeit) tatsächlich die einzigen konvexen Körper dieser Art (kongruente regelmäßige Seitenflächen, kongruente Ecken – die Regularität muss nicht vorausgesetzt werden).

(Ein vollständiger Beweis unter noch etwas schwächeren Voraussetzungen – für sphärische Polyeder – kann mit der eulerschen Polyederformel geführt werden.)

Kurz zusammengefasst: An einer Ecke können drei, vier oder fünf gleichseitige Dreiecke zusammenkommen. Auch drei Quadrate oder drei regelmäßige Fünfecke sind möglich. Weitere Möglichkeiten gibt es nicht.

Weitere Polyeder mit regelmäßigen Vielecken als Seitenflächen ergeben sich nur, wenn Vielecke mit unterschiedlicher Eckenzahl (aber eventuell gleicher Eckenart) zugelassen werden – dazu gehören unter anderem die archimedischen Körper - sowie Körper, bei denen nicht an jeder Ecke gleich viele Vielecke zusammentreffen.

Dualität

Verbindet man die Mittelpunkte benachbarter Seitenflächen eines platonischen Körpers, so erhält man (mit den Verbindungslinien als Kanten) wieder einen platonischen Körper, und zwar mit demselben Mittelpunkt. Dieser Körper wird als Dualkörper zum Ausgangskörper bezeichnet.

Auf Grund der Konstruktion ist klar, dass jeder Fläche des Ursprungskörpers jeweils eine Ecke des dualen Körpers entspricht. Außerdem entspricht jeder Kante, die zwei Flächen trennt, eine Kante, die zwei Ecken verbindet. Daraus ergibt sich, dass auch jeder Ecke des Ursprungskörpers jeweils eine Fläche des dualen Körpers entspricht. (Man kann sich das so verbildlichen, dass jede Fläche eine Ecke des Ursprungskörpers "abschneidet".)

Wiederholt man diese Konstruktion (konstruiert man also den zum Dualkörper dualen Körper), so erhält man einen (verkleinerten) platonischen Körper des Ausgangstyps mit gleichem Mittelpunkt.

Dabei bilden Hexaeder (Würfel) und Oktaeder sowie Dodekaeder und Ikosaeder jeweils ein duales Paar. Das Tetraeder ist zu sich selbst dual, wobei sich jedoch das duale Tetraeder in (verkleinerter) zentralsymmetrischer Lage befindet (d.h., er "steht auf dem Kopf").

Symmetrie

Die platonischen Körper zeigen größtmögliche Symmetrie:

• Ecken, Kanten und Flächen sind untereinander gleichartig, d.h. jede Ecke (Kante, Fläche) kann durch eine Symmetrie des Körpers auf jede andere Ecke (Kante, Fläche) abgebildet werden.

Man sagt dazu:

• Die Symmetriegruppe wirkt transitiv auf den Ecken, Kanten und Flächen.

Es gilt sogar:

• Die Symmetriegruppe wirkt transitiv auf den Fahnen. (Eine Fahne ist eine Ecke auf einer Kante auf einer Fläche.)

Die fünf platonischen Körper sind daher reguläre Polyeder. Die bei ihnen auftretenden Symmetriegruppen (und ihre Untergruppen) gehören zu den diskreten Raumgruppen. Duale platonische Körper haben dieselbe Symmetriegruppe. Das ist die Basis für die Konstruktion zahlreicher anderer Körper (z.B. der archimedischen Körper). Es gibt also nicht fünf, sondern nur drei dieser Gruppen: die Tetraedergruppe, die Würfelgruppe und die Ikosaedergruppe. Sie spielen in unterschiedlichen Zusammenhängen in der Mathematik eine Rolle.

Aufgrund ihrer symmetrischen Eigenschaften erfüllen alle platonischen Körper die Eigenschaft eines kubischen Kristalls. Ferner haben sie die Eigenschaft, dass sie bei einem Wurf mit exakt der gleichen Wahrscheinlichkeit auf jede ihrer Flächen fallen können.

Deltaeder

Da Tetraeder, Oktaeder und Ikosaeder auch zu den konvexen Deltaedern gehören, gehört aus jeder Symmetriegruppe ein Körper zu den Deltaedern.

Berührende Kugeln

Aus der hohen Symmetrie folgt unmittelbar: Jeder platonische Körper hat

• eine Inkugel, die alle seine Flächen berührt, und
• eine Umkugel, auf der alle seine Ecken liegen, sowie
• eine Kugel, auf der die Mittelpunkte der Kanten liegen.

Der gemeinsame Mittelpunkt dieser drei Kugeln ist der Mittelpunkt (oder das Zentrum) des platonischen Körpers.

Weitere mathematische Eigenschaften

Platonische Körper als reguläre Parkettierungen der Sphäre

Projiziert man die Kanten eines platonischen Körpers aus dem Mittelpunkt auf eine Kugel mit demselben Mittelpunkt (z.B. auf die Umkugel), so erhält man eine Parkettierung der Kugeloberfläche durch zueinander kongruente regelmäßige sphärische Vielecke, wobei in jeder Ecke gleich viele Kanten (unter gleichen Winkeln) zusammentreffen. Diese Parkettierungen haben dieselben Symmetrien wie der Ausgangskörper. Insbesondere sind sie ebenfalls fahnentransitiv. Es sind die fünf regulären Parkettierungen der Sphäre, zwischen denen dieselben Dualitätsbeziehungen bestehen wie zwischen den Körpern. (In anderem Zusammenhang spricht man auch von Landkarten und dualen Landkarten.)

Jede reguläre Parkettierung kann durch das Paar (p,q) beschrieben werden, wobei p für die Anzahl der Kanten eines Steines und q für die Anzahl der in einer Ecke endenden Kanten steht. Die platonischen Körper ergeben daher die dualen Paare (3,4) und (4,3), (3,5) und (5,3), sowie das selbstduale Paar (3,3). Dies sind alle Lösungen der Ungleichung

Diese Beziehung folgt aus dem eulerschen Polyedersatz, der die Anzahl der Flächen, Ecken und Kanten zueinander in Bezug stellt:

Flächen + Ecken = Kanten + 2 wobei die Konstante 2 für die Sphäre charakteristisch ist.

(Die Anzahl der Flächen ist (2 mal Kanten durch p), die der Ecken (2 mal Kanten durch q))

In der Ebene gilt (bei geeigneter Interpretation, nämlich asymptotisch)

Flächen + Ecken = Kanten

oder

mit den Lösungen

(4,4) (selbstdual), sowie (3,6) und dual dazu (6,3), welche für die drei regulären Parkettierungen der Ebene (durch Quadrate, Dreiecke und Sechsecke) stehen, die daher (in diesem Sinn) als Verallgemeinerung der platonischen Körper gelten können.

Die Lösungen von

liefern die regulären Parkettierungen der hyperbolischen Ebene.

Aus den platonischen Körpern abgeleitete Polyeder

Wegen der starken Regelmäßigkeit der platonischen Körper kann man leicht andere Körper von ihnen ableiten, die auch wieder sehr regelmäßig sind. Man muss dazu nur die gleichen Konstruktionen symmetrisch auf Flächen, Kanten oder Ecken anwenden. Ein Beispiel dafür sind die dualen Körper, die sich dadurch ergeben, dass man den Mittelpunkt jeder Fläche mit den Mittelpunkten der angrenzenden Flächen verbindet.

Einbeschreibungen

Es bestehen durchaus noch andere Möglichkeiten, einen platonischen Körper in einen anderen einzubauen.

Zum Beispiel erhält man ein Tetraeder, wenn man die Diagonale einer Würfelfläche als eine Kante verwendet, die dazu windschiefe Diagonale auf der gegenüberliegende Fläche als eine andere, und als die anderen vier Kanten die Diagonalen benutzt, die die Enden der beiden verbinden.

Ein Oktaeder erhält man, wenn man Flächen durch die Mittelpunkte der Kanten eines Tetraeders legt.

Aus einem Würfel erhält man ein Dodekaeder, wenn man auf jede Seitenfläche ein geeignetes Walmdach aufsetzt; umgekehrt erhält man durch eine passende Auswahl von Flächendiagonalen auf einem Dodekaeder den Würfel zurück:

Abgestumpfte platonische Körper

Wenn man von einem platonischen Körper ausgehend ein abgestumpftes Polyeder erzeugt, indem man seine Ecken so abschneidet, dass danach alle Kanten gleich lang sind, so erhält man einen halbregulären (archimedischen) Körper. Dieser Körper entsteht auch als Schnitt des platonischen Körpers mit seinem passend vergrößerten Dualkörper.

Archimedische Körper sind Beispiele für ziemlich regelmäßige Körper, bei denen Polygone verwendet werden, die zwar regelmäßig, aber von unterschiedlicher Seitenzahl sind.

Sternkörper

Baut man Pyramiden auf den Seitenflächen auf, anstatt abzuschneiden, erhält man Sternkörper, wie das Sterntetraeder.

Verwendet man für die Pyramiden gleichseitige Dreiecke, hat man Beispiele für Polyeder, die vollständig aus gleichen Polygonen bestehen, bei denen aber unterschiedlich viele in den Ecken zusammenstoßen.

Geschichtliches

Den Pythagoräern (6.Jh.v.Chr.) waren Tetraeder, Würfel, und Dodekaeder bekannt. Theaitetos (4.Jh.v.Chr.) kannte auch Oktaeder und Ikosaeder, wobei das Oktaeder vermutlich vorher nur deshalb nicht beachtet wurde, weil es als Doppelpyramide gesehen wurde. Der griechische Philosoph Platon (um 300 v.Chr.) hat die Körper später in seinem Werk Timaios ausführlich beschrieben und sie den Elementen des platonischen Weltbildes zugeordnet. Sie wurden in Platons Akademie intensiv untersucht und galten dort als Repräsentanten der Elemente, denen sie wie folgt zugeordnet wurden:

• Feuer: Tetraeder
• Wasser: Ikosaeder
• Luft: Oktaeder
• Erde: Würfel
• Äther / Quintessenz oder Geist: Dodekaeder

Davon leitet sich auch die alternative Bezeichnung kosmische Körper her.

Euklid (um 300 v.Chr.) konstruiert die platonischen Körper im XIII. Buch seiner Elemente. Das "XIV. Buch" (aus dem 2.Jh.v.Chr., Hypsikles) enthält einige Volumenberechnungen, und das "XV. Buch" (aus dem 6.Jh.n.Chr.) enthält weiteres Material zu ihnen.

Mit dem Aufkommen der Perspektive beschäftigten sich auch Künstler mit den platonischen Körpern (neben anderen regelmäßigen Körpern) und verwendeten sie dazu, ihre Fähigkeiten zu zeigen: u.a. Piero della Francesca, Leonardo da Vinci (Illustrationen zu Divina Proportione von Luca Pacioli), Albrecht Dürer, Wenzel Jamnitzer (Perspectiva Corporum Regularium, 1568).

Johannes Kepler gelang es (Mysterium Cosmographicum, 1596), die Bahnradien der sechs damals bekannten Planeten durch eine bestimmte Abfolge der fünf Körper und ihrer Innen- und Außenkugeln darzustellen. Diese Interpretation stimmt zwar ziemlich gut mit den damals bekannten ungenauen Werten überein, ihr entspricht aber keine astronomische Gesetzmäßigkeit.

Bei der Suche nach solchen Harmonien studiert Kepler in seinem Werk Harmonice Mundi (Weltharmonik) auch systematisch regelmäßige Körper und beschreibt neben den platonischen Körpern unter anderem auch die archimedischen Körper, sowie zwei nichtkonvexe regelmäßige Polyeder, sogenannte Sternkörper.

Platonische Körper jenseits der Mathematik

  Die auffällige Regelmäßigkeit macht die platonischen Körper auf vielerlei Art für den Menschen interessant.

• Zusätzlich zum klassischen, geometrischen Würfel, der leicht herzustellen ist und schon seit Jahrtausenden für Glücksspiele verwendet wurde, finden heute auch die anderen platonischen Körper (welche auch als Würfel bezeichnet werden) eine Anwendung im Spiel, z.B. im Fantasy-Rollenspiel (siehe Spielwürfel). Die Voraussetzungen dazu sind eine physikalisch gleichmäßige Dichteverteilung – also homogenes Material – sowie die gleichartige Beschaffenheit aller Ecken und Kanten.
• Platonische Körper sind seit langem Objekte Bildender Künstler. In der modernen Kunst hat sich vor allem M. C. Escher mit ihnen und ihnen ähnlichen regelmäßigen Körpern beschäftigt; auch Werke von Salvador Dali thematisieren platonische Körper oder ihre Entfaltung.
• Platonische Polyeder spielen auch eine wichtige Rolle im Adventure-Spiel The Dig.

Auch in der Natur können sich vorhandene Regelmäßigkeiten als platonische Körper ausprägen.

• Tetraeder, Würfel und Oktaeder kommen in der Natur als (idealisierte) Kristalle vor; dodekaedrische und ikosaedrische Symmetrieelemente finden sich bei Quasikristallen.
  
• Exakte Dodekaeder kommen nicht als Kristalle vor. Kristalle bestimmter Mineralien, wie z.B. Pyrit, die äußerlich wie ein Dodeakeder aussehen, sind KEINE exakten Pentagondodekaeder, sondern verzerrt. Allerdings ist die Verzerrung mit dem bloßen Auge aus der Entfernung oft nicht wahrzunehmen. Aus der Nähe betrachtet erkennt man jedoch, dass diese Körper nicht aus regelmäßigen (sondern unregelmäßigen) Fünfecken geformt sind.
  Zum Beispiel bilden Natriumchlorid und Alaun, das beim Ausfällen mit gewissen anderen Stoffen dotiert ist, Würfelkristalle. Reines Alaun kristallisiert als Oktaeder.
  Dabei ist die Abgrenzung zwischen den einzelnen Formen nicht absolut, sondern die interne Symmetrie kann sich in unterschiedlichen Ausprägungen äußern. In der Mineralogie fallen alle die platonischen Körper, Tetraeder, Würfel und Oktaeder; sowie Rhombendodekaeder, Kuboktaeder und ihre Mischformen; unter den Begriff kubisch. Nicht wenige Mineralien können dementsprechend mehrere dieser kubischen Formen annehmen. Dazu gehört zum Beispiel Pyrit, das sowohl als Würfel als auch als Oktaeder, oder wie oben beschrieben als verzerrtes Dodekaeder, vorkommt.
• Platonische Körper, im speziellen das Ikosaeder, sind sehr häufig Strukturformen, wie sie bei Clustern (also kleinen Nanoteilchen) beobachtet werden.
• Tetrahedran, Dodecahedran und Cuban sind organische Moleküle

• Über den Verwendungszweck des römischen Pentagondodekaeders wird bis heute spekuliert.

Siehe auch

• Catalanischer Körper
• Johnson-Körper