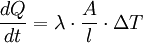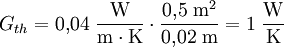Um alle Funktionen dieser Seite zu nutzen, aktivieren Sie bitte die Cookies in Ihrem Browser.
my.chemie.de
Mit einem my.chemie.de-Account haben Sie immer alles im Überblick - und können sich Ihre eigene Website und Ihren individuellen Newsletter konfigurieren.
- Meine Merkliste
- Meine gespeicherte Suche
- Meine gespeicherten Themen
- Meine Newsletter
WärmeleitfähigkeitDie Wärmeleitfähigkeit, auch Wärmeleitzahl (λ, k oder κ) eines Festkörpers, einer Flüssigkeit oder eines Gases ist bestimmt durch die Geschwindigkeit, mit der sich die Erwärmung an einem Punkt durch den Stoff ausbreitet. Die Wärmeleitfähigkeit ist also das Vermögen eines Stoffes, thermische Energie mittels Wärmeleitung in Form von Wärme zu transportieren. Die (spezifische) Wärmeleitfähigkeit in W/(K·m) ist eine temperaturabhängige Materialkonstante. Der Wärmeleitwert (Gth, absolute Wärmeleitfähigkeit) in W/K ist die von der Abmessung abhängige [Kennzahl]] eines Bauteils. Der Kehrwert der Wärmeleitfähigkeit ist der Wärmewiderstand für die Anwendung des Ohmschen Gesetzes des thermischen Kreises. Produkt-Highlight
FestkörperBei Festkörpern ist der Wärmestrom bzw. Wärmefluss in erster Näherung direkt proportional zum Temperaturunterschied ΔT an den beiden betrachteten Enden, der in Kelvin oder Grad Celsius gemessen wird. Der Wärmestrom selber wird in Joule pro Sekunde oder Watt angegeben. Die Einheit der Wärmeleitfähigkeit ergibt sich aus J/(m·s·K) bzw. W/(m·K):
Als Faustregel gilt: Was elektrischen Strom gut leitet (Silber, Kupfer), leitet auch Wärme gut (Wiedemann-Franzsches Gesetz). Der Umkehrschluß ist allerdings oft falsch, deutliches Gegenbeispiel ist bsp. der sehr gut wärmeleitende Diamant. KunststoffeBei Kunststoffen findet Wärmetransport durch Schwingungen (Phononen) der Polymerketten statt. Die Wärme wird durch Fortpflanzung der elastischen Gitterschwingungen über kovalente Bindungen entlang der Polymerketten transportiert sowie über Nebenvalenzbindungen übertragen. RechenbeispielDie (spezifische) Wärmeleitfähigkeit ist die Eigenschaft eines Materials. Für einen Körper mit festen Abmessungen kann dementsprechend ein (absoluter) Wärmeleitwert berechnet werden. Für eine Platte aus Polystyrolschaum (eine Handelsbezeichnung: Styropor) mit den Abmessungen 50 cm Breite, 1 m Höhe und 2 cm Tiefe ergibt sich beispielsweise:
Bei einem Kelvin Temperaturunterschied zwischen Ober und Unterseite der Styroporplatte fließt also ein Wärmestrom von 1 Joule pro Sekunde durch die Platte. Flüssigkeiten und GaseBei Flüssigkeiten und Gasen variiert die Wärmeleitfähigkeit etwas mit dem Druck und stark mit der Temperatur. Allerdings reicht die Kenntnis der Wärmeleitfähigkeit allein nicht aus, um den Transport von Wärme von der wärmeabgebenden oder aufnehmenden Fläche auf die Flüssigkeit oder das Gas zu beschreiben. Vielmehr ist der Strömungszustand von Bedeutung. Die genauen Verhältnisse sind zwar oft unbekannt, aber weil die Vorgänge technisch wichtig sind, ist darüber geforscht worden und natürlich auch viel gemessen worden. Dabei ist interessant und hilfreich, dass man alleine aus der Dimensionsanalyse der auftretenden Größen heraus argumentieren kann, dass die Werte von dimensionslosen Kenngrößen abhängen müssen. Dies erlaubt zum einen eine Einschränkung der in Frage kommenden Abhängigkeiten, zum anderen ein Übertragen von Modellversuchen auf die kleinere oder auch größere Realität. Typisches Beispiel ist der Wärmeübergang zwischen einem Rohr und einer Flüssigkeit, der abhängig sein muss von der Wärmeleitfähigkeit der Flüssigkeit, von der Wärmekapazität, von den Abmessungen des Rohres, von der Entfernung vom Rohreinlauf und den Bedingungen am Einlauf und von der Strömungsgeschwindigkeit. Weil die Wärmeleitfähigkeit von Gasen, insbesondere von Luft bei Umgebungstemperatur verglichen mit den Wärmeleitwerten der typischen Baustoffe klein ist, nutzt man diese zur Begrenzung der Wärmeverluste, indem man Luftschichten anordnet. Allein dadurch, dass Luft sich bei Erwärmung ausdehnt und damit einen Auftrieb erzeugt (wird beim Heißluftballon ausgenutzt), kommt eine Strömung zustande, die den Wärmedämmeffekt stört. Dies wird die üblichen Temperaturdifferenzen, wie sie am Gebäude auftreten, bei Schichtdicken unter 40 mm stark rückläufig und spielt bei 10 mm nur noch eine untergeordnete Rolle. Allerdings wird bei Diskussionen häufig vergessen, dass ein wesentlicher Teil der Wärme durch Strahlung ausgetauscht wird. Bei einem Wärmedämmstoff ist es folglich wichtig, dass die Strahlung vom Feststoff aufgefangen und wieder abgegeben wird. Das führt sozusagen zu einem Widerstand für die Strahlung, so dass insgesamt weniger Energie durch Strahlung transportiert werden kann. Genauer: wenn zwischen zwei Scheiben ein Strahlungsaustausch besteht, dann ist dafür eine Temperaturdifferenz zwischen den Scheiben verantwortlich. Die Wärmemenge ist zumindest bei kleinen Temperaturdifferenzen von einigen Grad linear von der Temperaturdifferenz abhängig. Schaltet man nun eine dritte Wand, eine Folie zwischen beide Scheiben ein, dann nimmt diese eine mittlere Temperatur ein, so dass zwischen Folie und Scheibe auch nur die Hälfte der Wärme durch Strahlung transportiert werden kann. Dies gilt auf beiden Seiten der Folie, so dass der Einzug der Folie die Wärmeleitung durch Strahlung auf die Hälfte reduziert. Das Einbringen von strahlungsundurchlässigem Material macht nur Sinn, wenn dieses nicht kompakt ist, die Hohlräume also in Relation zur Wellenlänge der Strahlung groß genug sind. Ferner darf die Wärmeleitung nicht die Gewinne bei der unterdrückten Strahlung „auffressen“ und zu guter Letzt muss für die Luft, die den Raum in den Poren füllt auch noch Platz vorhanden sein. Es sind „Superdämmstoffe“ denkbar, die auf die Luft als trennendes Medium verzichten, doch dafür muss ein Ersatz gefunden werden. Dieser Ersatz muss die durch den äußeren Luftdruck entstehenden Kräfte aufnehmen, also Kraft leiten, und auch der Ersatz leitet Wärme. Strahlungswärme kann durch passende Oberflächen, die weniger Strahlung aufnehmen und emittieren, verringert werden. Ein gutes Beispiel sind Vakuumkollektoren, bei denen man beide Techniken anwendet. Aus anwendungstechnischer Sicht heraus unterscheidet man die unterschiedlichen Mechanismen nicht, sondern gibt einen globalen Wert an, der für die typischen Temperaturen hinreichend genau zutrifft. Man unterscheidet z.B. bei Dämmstoffen nicht einmal sonderlich genau, sondern fasst diese in Gruppen zusammen, die bestimmte Anforderungen erfüllen müssen. Dieses hat den Vorteil, dass bei einer Planung nun nicht etwa der genaue Dämmstoff benannt werden muss, sondern dass die Angabe der Wärmedämmstoffgruppe ausreichend ist. Damit kann die konkrete Wahl des Dämmstoffes dann während der Bauphase erfolgen, was hinsichtlich Preis und Verfügbarkeit von Vorteil ist. Die Ausbreitung von Wärme im Gas ist durch die kinetische Gastheorie gut verstanden, die Ausbreitung im Raum durch Strahlung ist ebenfalls recht gut verstanden, die Ausbreitung in Festkörpern und Flüssigkeiten ist komplizierter. Insgesamt bleibt festzustellen, dass Wärmeleitung und Wärmestrahlung sich auf einer elementaren Ebene abspielen und folglich Quantentheoretische Effekte sind. Licht ist Wärmestrahlung und Strahlung wird als Teilchen mit einem Energiequant aufgefasst. Damit wird ein Phänomen, das in Praxis eigentlich einfach erscheint, dann doch Gegenstand einer für den Laien kompliziert erscheinenden Theorie. Ein solches Beispiel für unerwartete quantentheoretische Effekte der Wärmeleitung mag Helium im flüssigen Zustand sein. SuprafluideSuprafluide Flüssigkeiten, beispielsweise Helium II unter 2,17 Kelvin, haben aufgrund ihres makroskopischen Quantenzustandes hingegen eine (fast) unendliche Wärmeleitfähigkeit. Dies begründet sich damit, dass das eigentlich für die Wärmeleitung verantwortliche Valenzband bei Helium II fehlt. Dabei gleichen die Formeln zur Berechnung der Geschwindigkeit des Wärmeflusses eher denen der Schallausbreitung in Luft. In Helium II bei 1,8 Kelvin bewegt sich Wärme mit etwa 20 m/s in Wellenform. Dieses Phänomen heißt zweiter Schall. VakuumIm Vakuum findet keine Wärmeleitung statt, der Wärmetransport geschieht nur durch Wärmestrahlung. Dieses wird zum Beispiel bei der Thermosflasche ausgenutzt, um einen sehr geringen Wärmetransport zu erreichen. Um auch den Energietransport per Wärmestrahlung zu minimieren, sind die dem Vakuum zugewandten Flächen des zur Isolation verwendeten Glas- oder Stahlkörpers hochverspiegelt. Wärmeleitfähigkeit im BauwesenDie Wärmeleitfähigkeit λ ist eine Stoffkonstante bei einem definierten Umgebungsklima (Temperatur und Luftfeuchte) und wird deswegen eigentlich mit einem Index versehen: λ20 / 50 oder auch λ23 / 80;λdry BeispieleEinige Beispiele zum Rechenwert der Wärmeleitfähigkeit für Baustoffe, sonstige Festkörper, Flüssigkeiten (alle bei Raumtemperatur) und Gase (bei 0 Grad Celsius). Eine höhere Wärmeleitfähigkeit bedeutet eine bessere (schnellere) Wärmeübertragung.
Siehe auch
Kategorien: Werkstoffeigenschaft | Stoffeigenschaft |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dieser Artikel basiert auf dem Artikel Wärmeleitfähigkeit aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation. In der Wikipedia ist eine Liste der Autoren verfügbar. |




![\lambda = {Q \cdot l \over A \cdot t \cdot \Delta T } = {{[J] \cdot [m]} \over {[m^2] \cdot [s] \cdot [K]}}](images/math/4/f/6/4f677aad66bb2ec0a5e5fad0ffa11d97.png)
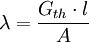
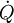 in
in