Kontrollierbarkeit der Ionisierungsenergie von Atomen verspricht Fortschritte in der chemischen Synthese
Die Ionisierungsenergie ist eine der wichtigsten physikalisch-chemischen Größen. Sie ist definiert als die Energiemenge, die benötigt wird, um ein Elektron aus einem Atom zu reißen. Die Abhängigkeit der Ionisierungsenergie von der Ordnungszahl bestimmt das Periodengesetz der chemischen Elemente, das als grundsätzlich konstant angenommen wird. Basierend auf dem zuvor vorhergesagten Effekt der Veränderung der Elektronenmasse zeigte das Forscherteam, dass die Ionisierungsenergie von Atomen, die in photonischen Kristallen mit einem ultrahohen Brechungsindex platziert sind, signifikant verändert werden kann.
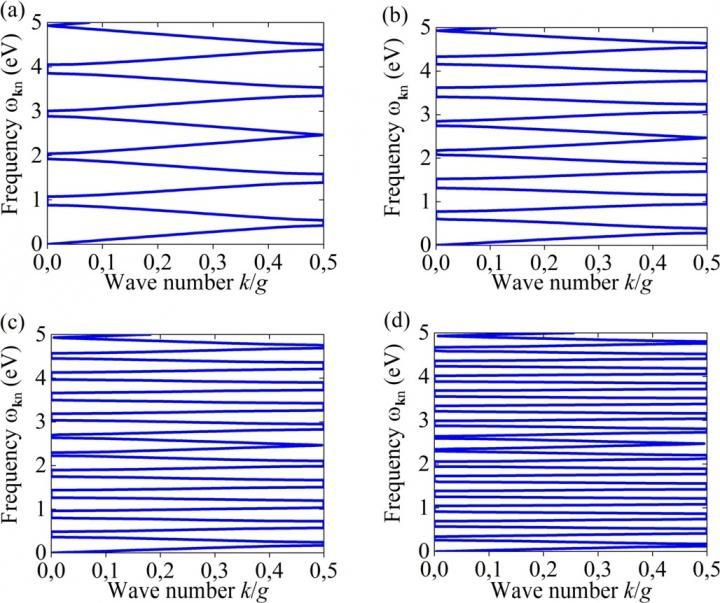
Dispersionsbeziehungen für TM-Bloch-Moden in eindimensionalem PC für verschiedene Werte des Brechungsindex (a) nh = 2, (b) nh = 3, (c) nh = 5, (d) nh = 7. Die Anzahl der Bänder n in den Dispersionsbeziehungen steigt linear mit dem Brechungsindex des PC-Materials.
Kazan Federal University
Photonische Kristalle sind Medien mit periodisch wechselnden elektromagnetischen Eigenschaften. Ein Beispiel für einen photonischen Kristall ist eine dichte Packung von dielektrischen Mikrokugeln, zwischen denen sich ein leerer Raum befindet. Die Größe dieser Leerräume ist groß genug, um ein dort platziertes Elektron oder ein Atom als frei von Wechselwirkungen mit dem Material der Wände zu betrachten. Dennoch beeinflusst die Umgebung der photonischen Kristalle indirekt die Eigenschaften der Teilchen, indem sie deren eigenes Strahlungsfeld modifiziert.
Tatsache ist, dass nach dem modernen Weltbild alle Teilchen an Vakuumquantenfluktuationen teilnehmen. Insbesondere erzeugt ein Elektron ständig virtuelle Photonen und vernichtet sie sofort wieder. Es stellte sich heraus, dass photonische Kristalle in der Lage sind, diese Wechselwirkung zu beeinflussen. Traditionell wurde diese Frage nur für in einem Atom gebundene Elektronen untersucht. Ein Atom, das an einem solchen Prozess teilnimmt, erhält eine Korrektur seiner Energie, die Lamb-Verschiebung genannt wird und im Verhältnis zu den Atomenergien selbst sehr klein ist, auch wenn das Atom in photonischen Kristallen platziert ist.
Der Grund, warum niemand die Quantenfluktuationen eines freien Elektrons in einem photonischen Kristall betrachtet hat, ist, dass seine Masse in diesem Zustand gleich unendlich ist. Tatsache ist, dass die Masse eines freien Elektrons aufgrund der Wechselwirkung mit dem Vakuum eine Korrektur erhalten muss, die als elektromagnetische Masse bezeichnet wird. Diese Korrektur wird zu der "nackten" Masse des Elektrons addiert und bildet seine faktisch beobachtete Masse.
Berechnungen, die in der ersten Hälfte des 20. Jahrhunderts durchgeführt wurden, zeigten jedoch, dass die Integrale in den Formeln für die elektromagnetische Masse divergieren. Jahrhunderts zeigten jedoch, dass die Integrale in den Formeln für die elektromagnetische Masse divergieren. Um dieses Problem zu umgehen, entwickelten die Physiker ein Renormierungsverfahren für die Masse, das darin bestand, die elektromagnetische Masse zu ignorieren und in allen anderen Formeln die "bloße" Masse des Teilchens durch die beobachtete Masse zu ersetzen. Dies ebnete den Weg zur Quantenelektrodynamik, deren Vorhersagen unter gewöhnlichen Bedingungen in Experimenten mit hoher Genauigkeit bestätigt werden.
Wenn jedoch photonische Kristalle die Wechselwirkung mit dem Vakuum beeinflussen, sollte sich dies in der elektromagnetischen Masse und damit in der tatsächlich beobachteten Elektronenmasse niederschlagen. Die Forscher zeigten, dass sich in diesem Fall eine endgültige Korrektur ergibt, die gleich der Differenz zwischen den elektromagnetischen Massen eines Elektrons in einem photonischen Kristall und im Vakuum ist. Außerdem ist die Masse aufgrund der Anisotropie des photonischen Kristalls abhängig von der Richtung, in die das Elektron fliegt. Dies führt dazu, dass ein in einem Atom gebundenes Elektron neue Energiekorrekturen hat, die von seinem Zustand abhängen. Es stellte sich heraus, dass für sehr hohe Brechungsindizes der Substanz, aus der der photonische Kristall besteht, diese Korrekturen vergleichbar werden mit den Energien der Übergänge zwischen den Niveaus, einschließlich der Energien der Ionisationsübergänge.
In dieser Arbeit berechneten sie Korrekturen der Ionisierungsenergie von Wasserstoff- und Alkaliatomen, die sich in den Hohlräumen eines eindimensionalen photonischen Kristalls aus Materialien mit einem ultrahohen Brechungsindex befinden. Es zeigte sich, dass die Abnahme der Ionisierungsenergie im Fall des Cäsiumatoms 68 Prozent erreichen kann.
Der vorhergesagte Effekt ist sowohl für die grundlegende als auch für die angewandte Physik und Chemie von großer Bedeutung. Insbesondere wurde zum ersten Mal eine Methode zur Manipulation der elektromagnetischen Masse vorgeschlagen. Darüber hinaus erlaubt der Effekt eine Beeinflussung des Periodengesetzes der chemischen Elemente, und gerade die Veränderung der Ionisierungsenergie kann genutzt werden, um neue chemische Verbindungen zu synthetisieren und darauf basierende Medikamente herzustellen.
Für die Zukunft plant das Team, mit großen pharmazeutischen Zentren zusammenzuarbeiten und die Möglichkeit der Nutzung für die Synthese neuer Verbindungen zu untersuchen. Eine experimentelle Verifizierung des Effekts kann durch die Messung der Geschwindigkeit einer chemischen Reaktion erfolgen, die in der Gasphase zwischen den Wänden eines eindimensionalen photonischen Kristalls stattfindet. Darüber hinaus wollen sie die Korrektur der Ionisierungsenergie für andere chemische Elemente berechnen.
Hinweis: Dieser Artikel wurde mit einem Computersystem ohne menschlichen Eingriff übersetzt. LUMITOS bietet diese automatischen Übersetzungen an, um eine größere Bandbreite an aktuellen Nachrichten zu präsentieren. Da dieser Artikel mit automatischer Übersetzung übersetzt wurde, ist es möglich, dass er Fehler im Vokabular, in der Syntax oder in der Grammatik enthält. Den ursprünglichen Artikel in Englisch finden Sie hier.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
Meistgelesene News
Weitere News von unseren anderen Portalen
Verwandte Inhalte finden Sie in den Themenwelten
Themenwelt Synthese
Die chemische Synthese steht im Zentrum der modernen Chemie und ermöglicht die gezielte Herstellung von Molekülen mit spezifischen Eigenschaften. Durch das Zusammenführen von Ausgangsstoffen in definierten Reaktionsbedingungen können Chemiker eine breite Palette von Verbindungen erstellen, von einfachen Molekülen bis hin zu komplexen Wirkstoffen.
Themenwelt Synthese
Die chemische Synthese steht im Zentrum der modernen Chemie und ermöglicht die gezielte Herstellung von Molekülen mit spezifischen Eigenschaften. Durch das Zusammenführen von Ausgangsstoffen in definierten Reaktionsbedingungen können Chemiker eine breite Palette von Verbindungen erstellen, von einfachen Molekülen bis hin zu komplexen Wirkstoffen.
